“幾何畫板”與數學課堂的有效整合
浙江 蘇玲玲
“幾何畫板”與數學課堂的有效整合
浙江 蘇玲玲
1 寓美于教,培養學習興趣
案例1:美麗的勾股樹
學習了“探索勾股定理”后,可向學生展示美麗的勾股樹。并讓學生課后嘗試提出一些問題,同伴相互交流。(可作適當的提示,如讓學生思考每長一次得到的正方形的面積與原正方形的面積有何關系,長n次后有多少個正方形,)
說明:美麗的勾股樹可通過參數的增減改變伸長的次數(如下圖),可以無限伸長。還可以通過動畫左右擺動,猶如可愛的小牛晃動著腦袋。
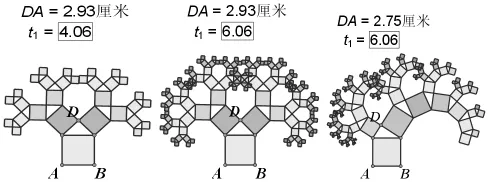
評析:通過上述“幾何畫板”操作充分展示了數學圖形的美,讓學生看后心曠神怡、浮想聯翩。激起了學習的好奇心和內心探索未知世界的欲望,以飽滿的熱情投入到數學學習中。而在學生的探索中,不僅能及時鞏固所學知識,還增強了學生發現問題、提出問題、分析問題、解決問題的能力,同時培養了學生自主探索能力和合作交流意識。真正做到了知識與技能、方法與過程、情感態度與價值觀“三維目標”的和諧統一。
2 突破靜態思維的束縛
“幾何畫板”呈現的動態圖形比黑板上的靜態圖形更能引起學生主動學習的興趣,激發學生發現的動機。
案例2:(1)如圖(1),在正方形ABCD中,點E在BC邊上移動,∠EAF=45°,AF交CD于點F,連結EF。試探索BE、DF、EF三條線段的數量關系,并說明理由。
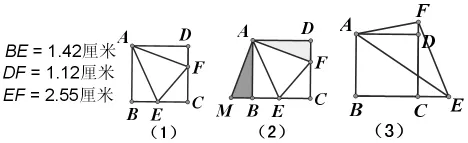
說明:用“幾何畫板”作出圖形,經度量驗證,容易得出EF=BE+DF,如何添加輔助線,將三條線段構造到一對全等三角形中是本題的關鍵所在。接著將△ADF繞點A順時針旋轉90°,全等變換得到圖(2),可將BE和DF轉化到同一直線上。于是容易得到證明思路。
(2)若點E在BC的延長線上,如圖(3)所示,上面BE、DF、EF三條線段關系的結論還成立嗎?
在幾何畫板中,拖動點E至BC延長線上,觀察圖形的變化。由于有了(1)的基礎,(2)可以放手讓學生自己去研究。通過“幾何畫板”的動態演示,使學生更直觀的從感性上對圖形探究性問題有了深刻的認識,克服認知過程中的困難,開闊了視野和思路,有利于學生學習能力的發展和提高。
3 增強學生提出問題的能力
運用“幾何畫板”動手試一試、做一做,手腦并用,獲得直接的感性認識,通過動手操作自主探索知識,能最大限度的發揮直觀能動性,并能由此引發奇思妙想,產生大膽的猜想和創新,從而自主地提出有價值的數學問題。
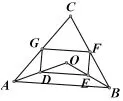
案例3:如圖,已知點O是△ABC內一點,D、E、F、G分別是AO、BO、CB、CA的中點。你認為四邊形DEFG是平行四邊形嗎?請說明理由。
操作一:教師在完成上述問題后利用“幾何畫板”
任意拖動點O,讓學生觀察發現問題,
從而學生可能會提出一下問題。
變式1:無論點O在什么位置(不與點C重合),問題中的結論都成立。
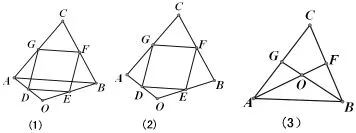
操作二:教師再利用“幾何畫板”中的隱藏功能隱去線段AB,讓學生觀察能發現什么?
變式2:如圖(2),已知D、E、F、G分別是四邊形AOBC四邊的中點,四邊形DEFG是平行四邊形嗎?請說明理由
操作三:連結線段AF、BG記交點為點O,并測量OFOA的長度,讓學生觀察發現了什么?從而提出變式問題。
變式3:如圖(3),AF、BG是△ABC邊BC、AC上的中線,AF、BG相較于點O,你認為AO、OF的長度有何關系,請說明理由。
評析:由于在平時的教學中比較注重解題的能力,學生提出問題的能力比較缺乏。當然,提出問題能力的形成不能一蹴而就,更不能搞突擊,應滲透在教學過程中。案例3中,借助“幾何畫板”,通過改變圖形中的一些元素的位置發現新的問題,這是培養學生提出問題能力行之有效的途徑。
4 有效實現將抽象知識形象化
數學理論的表述往往是抽象的,而圖形則以其生動、直觀的形象展現于人們的面前,以幫助理解、記憶抽象的數學內容。“數形結合”是學習數學的重要方法,用圖形解釋抽象的問題更直觀。學生學習函數圖象性質時,由于變化的抽象性,對其很難理解,利用“幾何畫板”就很容易解決這一問題。
案例4:一次函數圖象的性質
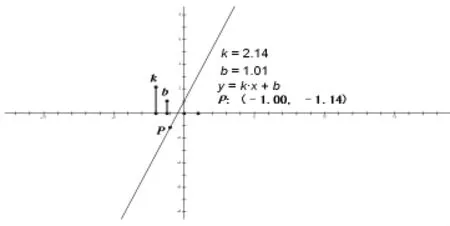
一次函數圖象的性質,不僅很抽象,還需要將數與形有效結合。如果僅是通過講解,很難讓學生接受,學生只能是死記硬背各條性質,極易挫傷學生學習的熱情。“幾何畫板”使靜態變為動態,巧妙地將數量變化與圖形變化有效結合,從而促進學生對知識的理解與記憶。
操作一:上下移動改變k的大小,觀察變化規律。
操作二:上下移動改變b的大小,觀察圖形的變化規律。
操作三:同時改變k、b的大小,觀察圖形的變化規律。
操作四:拖動點P,觀察點P的坐標x,y的變化規律。(1)當k>0時如何變化,(2)當k<0時如何變化
最后學生在觀察、猜想、分析后自主歸納出一次函數圖像的性質。
案例5:探索二次函數圖象開口方向、對稱軸位置及在y軸上的交點與之間的關系。
操作一:改變的值觀察二次函數圖象的運動情況。
操作二:改變b的值觀察二次函數圖像的運動情況
操作三:改變c的值觀察二次函數圖象的運動情況,
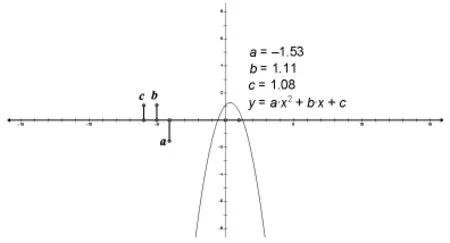
通過分別改變的值,看到了圖象運動的規律,從而要求學生討論歸納并填寫下表:
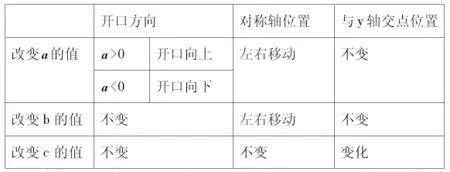
結論:開口方向:當>0時,開口向上;當<0時,開口向下;當的絕對值越大時,開口越小,反之亦然;對稱軸位置:改變,b的值,對稱軸位置都會變化,改變c的值,對稱軸位置不變;與y軸的交點:改變、b的值,圖像與y軸的交點不變,當改變c的值時,圖象與y軸的交點會變化,當c的絕對值越大時,離原點越遠。
(作者單位:水頭鎮第一中學)
(編輯 王旸)

