連續時間信號頻譜分析研究及MATLAB實現

井敏英 郭佳林 李大偉 段 濤

（陜西理工學院，陜西 漢中 723001）

連續時間信號頻譜分析研究及MATLAB實現

井敏英 郭佳林 李大偉 段 濤

（陜西理工學院，陜西 漢中 723001）

信號的頻譜分析是信號與系統分析的基礎。文章分析了用數值計算的方法實現確知連續時間信號的頻譜分析，即采用離散傅里葉變換的快速算法實現對連續信號的頻譜估計，然后在 MATLAB語言工具下結合正弦信號給出了頻譜分析的結果。

頻譜分析；離散傅里葉變化；MATLAB

（一）引言

在信號處理過程中，頻域分析方法往往比時域分析方法更方便和有效。對于確知連續時間信號，其頻域分析可以通過連續時間傅里葉變換來進行，但是，這樣計算出來的結果仍然是連續函數，計算機不能直接加以處理。為了實現數值計算，還需要對其進行離散化處理，即采用離散傅里葉變換（DFT）進行分析。DFT的快速算法的出現，使DFT在數字通信、圖像處理、功率譜估計、系統分析與仿真、雷達信號處理、光學、醫學等各個領域都得到廣泛應用。本文以正弦信號為例，介紹用DFT的快速算法即快速傅里葉變化（FFT）實現確知連續時間信號的頻譜分析，給出了MATLAB語言工具下的分析程序。

（二）信號頻譜分析的原理

對于時間連續信號f(t)，其頻譜分析可以通過連續時間傅里葉變換（CTFT）來進行。連續時間傅里葉變化特別適合于對時間連續信號的理論分析，但是，由于函數f(t)和其頻譜函數都是連續函數，不能夠直接用計算機來處理，因此在進行數值計算時必須將其離散化，然后利用離散傅里葉變換（DFT）實現近似計算。

設對連續時間信號 f(t)的截取時間段長度為L，對其進行離散化的采樣時間間隔為T，那么采樣輸出的離散時間序列f( nT)中的信號樣值點數N為：

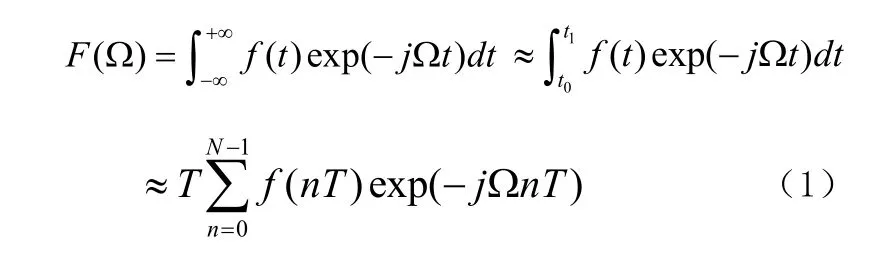
但是，這樣計算出來的結果F( Ω)仍然是連續函數，計算機不能直接加以處理。為了實現數值計算，還需要對F(Ω)進行離散化處理。將頻率段0～1/THz劃分為N個計算頻率點，這N個離散頻率點以角頻率表示為：

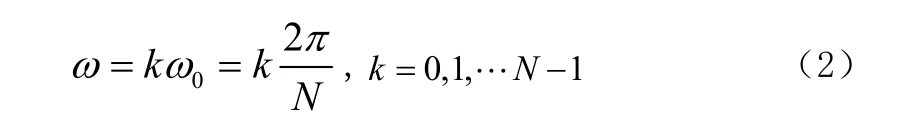
即得到離散頻率點上的近似計算式：

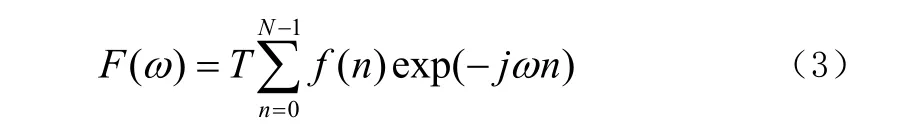
對比DFT計算式，顯然有

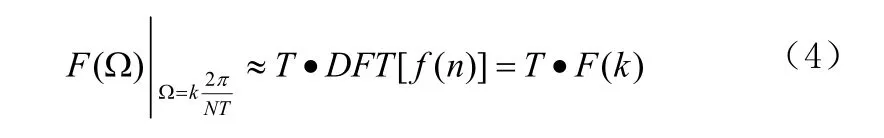
該式表明，利用DFT(FFT)計算連續時間傅里葉變換的頻譜時，除了計算時域樣點的離散傅里葉變化的頻譜F( k)，還要將F( k)乘以取樣時間間隔T，才能得出結果。

（三）頻譜分析的若干問題討論

通過以上原理可知，連續非周期信號頻譜的數值計算必須首先對信號時域采樣，得到時間離散化的信號，時域采樣必須滿足或近似滿足采樣定理。根據時域頻域的對應關系，時域采樣將導致所得的抽樣信號頻譜周期化。然而，為了使周期化后的抽樣信號頻譜便于計算機處理，還必須再將其頻域離散化，方法是對該頻譜進行頻域采樣。根據時域頻域的對應關系，頻域離散化將對應于時域信號的周期化。因此，對于連續非周期信號頻譜進行數值計算時，要確定如何截取信號的時間段、如何選擇時域采樣率，以及在時間段上對信號進行截取的方式。截取信號的時間段長度決定了時域周期化的周期，對應于頻率抽樣的頻率間隔，即頻率分辨率；時域采樣率決定了頻域周期化的周期，即頻譜數值計算的范圍；而在某時間段上對信號進行截取的方式，即不同窗函數的應用，決定了信號頻譜估計的精度和有效范圍。設要分析連續時間非周期信號f(t)在頻率范圍內的頻譜，且要求分析的頻譜分辨率（數值計算的頻率間隔）為Δf，則首先應根據信號頻率范圍確定采樣率，在根據所要求的頻率分辨率確定截取時間長度，從而計算出所需計算FFT的序列長度（點數），最后根據信號時域波形特性選擇使用不同的窗函數。

1.根據分析的信號頻率范圍確定采樣率。要分析信號在頻率范圍內的頻譜，則采樣率必須滿足采樣定理，即相應地，采樣時間間隔T（也稱為時間分辨率）滿足

2.根據頻率分辨率要求確定分析信號 f(t)的截取時間長度。要使所分析的頻率分辨率達到Δf，即每隔Δf計算一個頻率點，那么對信號的截取時間長度L必須滿足L≥1/Δf，根據截取時間長度L和采樣時間間隔T就可以計算出截取時間信號離散化之后的序列點數N，也可以由計算采樣率 fs和頻率間隔Δf來等價計算出序列點數，即：

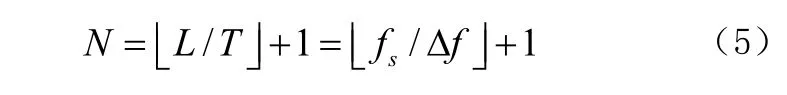
3.根據信號時域波形特性來應用不同的窗函數。使用窗函數可以控制頻譜主瓣寬度、旁瓣抑制度等參數，從而更好地進行波形頻譜分析和濾波器參數的設計。將窗函數與信號的時域波形或頻譜進行相乘的過程，就稱為對信號做時域加窗和頻域加窗。不同窗函數與信號時域波形相乘就是以不同窗函數對時間無限長的連續信號f(t)進行時間段截取。

（四）分析實例

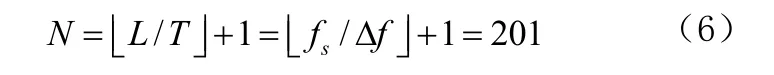
現應用MATLAB語言工具，使用數值計算的方法對其進行頻譜估計。分別用矩形窗、漢明窗和漢寧窗進行時域加窗，分析信號幅度譜曲線，程序代碼如下：

圖1 3種加窗后的幅度頻譜圖

可以看出，圖1中3種加窗后對信號的頻譜估計與理論值都有一定的誤差，這是由于在實際分析過程中，要對連續信號采樣和截斷。加矩形窗的頻譜誤差最大，那是因為事實上，加矩形窗等價于截取時不作加窗處理。從圖1中3種加窗后的幅度譜估計曲線來看，應用漢明窗和漢寧窗都比應用矩形窗（等價于不加窗）的估計精度要高。

（五）結論

以上對帶限確知連續時間信號的頻譜分析的數值計算方法進行了分析，在分析過程中要對信號進行采樣和截斷，因此會出現一定誤差，但只要合理選擇分析參數可以使誤差在工程允許的范圍之內。對于隨機信號，由于是無限大能量的功率信號，它不滿足傅里葉變換條件，而且也不存在解析表達式，因此就不能夠應用確知信號的頻譜計算方法去分析隨機信號的頻譜。但可以用以上確知信號頻譜分析的方法分析隨機信號的功率譜，因此同樣適應于隨機信號的頻域研究。

[1]高西全,丁玉美.數字信號處理[M].西安:西安電子科技大學出版社,2010.90-110.

[2]邵玉斌.Matlab/Simulink通信系統建模與仿真實例分析[M].北京:清華大學出版社,2008:166-180.

[3]張登奇,楊慧銀.信號的頻譜分析及 MATLAB實現[J].湖南理工學院學報(自然科學版),2010,23(3):29-33.

TN911.6

A

1008-1151(2011)04-0042-02

2011-01-18

井敏英（1978－），女，陜西富平人，陜西理工學院物理系碩士，從事通信信號處理的研究。