“亞黃金橢圓”的若干性質(zhì)

●

(秦安縣第二中學(xué) 甘肅天水 741600)

“亞黃金橢圓”的若干性質(zhì)

●羅文軍

(秦安縣第二中學(xué) 甘肅天水 741600)

0 引言

黃金橢圓中有許多美好的性質(zhì).同樣地，亞黃金橢圓也有許多美好的性質(zhì).本文通過對亞黃金橢圓的部分性質(zhì)作一些探討，以期達(dá)到對圓錐曲線中更多的特殊性質(zhì)進(jìn)一步地挖掘和探索，同時對中學(xué)生更深入地學(xué)習(xí)圓錐曲線起引導(dǎo)作用.

為了探討亞黃金橢圓性質(zhì)的需要，這里對這個特殊橢圓的一些概念作些說明.

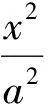
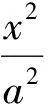
1 亞黃金橢圓的定義

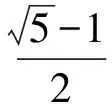
2 亞黃金橢圓性質(zhì)的探究

性質(zhì)1在亞黃金橢圓中，2條互為共軛直徑所在直線的斜率(斜率存在)之積為-e2.

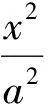
得

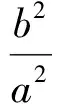
因為在亞黃金橢圓中c2=ab,所以

c4=a2b2,

從而

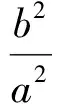
證明設(shè)P(x0,y0),則|OM|=|x0|,對b2x2+a2y2=a2b2的2邊關(guān)于x求導(dǎo)，得

2b2x+2a2yy′=0,

從而

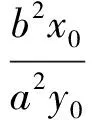
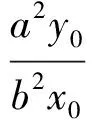
于是

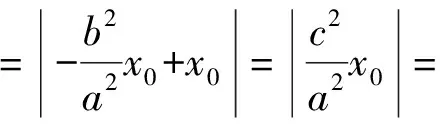
得

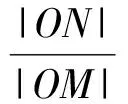
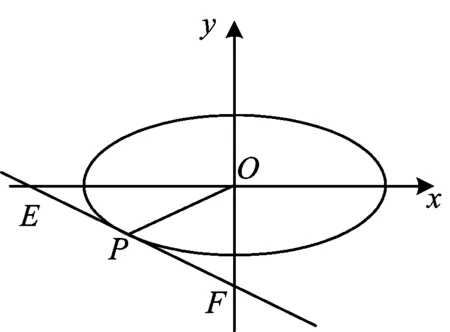
圖1

性質(zhì)3不平行于亞黃金橢圓對稱軸的切線斜率與經(jīng)過該切點和中心的直線斜率之積為-e4.

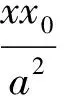
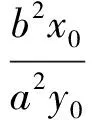
從而

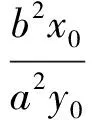
因此

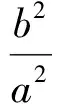
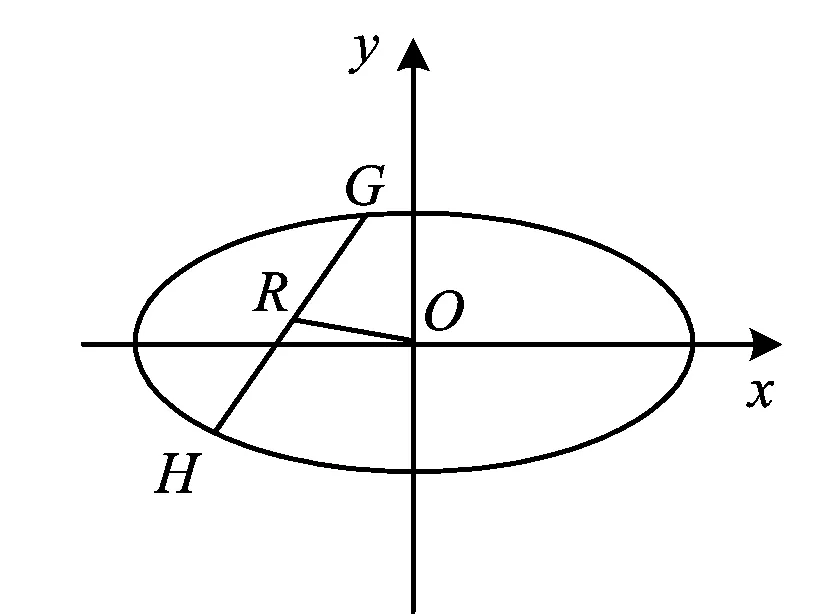
圖2

性質(zhì)4不平行于亞黃金橢圓對稱軸且不經(jīng)過橢圓中心的弦所在直線的斜率與經(jīng)過該弦中點和橢圓中心的直線斜率之積為-e4.

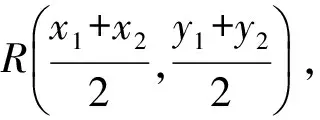
因此

(1)

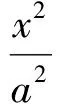
將式(2)，式(3)代入式(1)，得

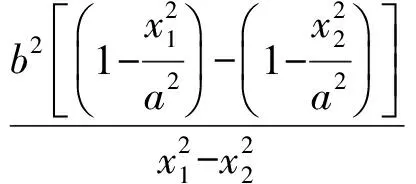
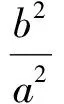
圖3

性質(zhì)5如圖3，MN是經(jīng)過亞黃金橢圓中心的弦，T是亞黃金橢圓上任意一點(頂點除外)，若TM,TN的斜率都存在且不為0，則kTM·kTN=-e4.

證明設(shè)M(x0,y0),任意一點T(x′,y′),則N(-x0,-y0).由題意得

因此

(4)

因為T,M是亞黃金橢圓上的點，所以

將式(5)，式(6)代入式(4)，得

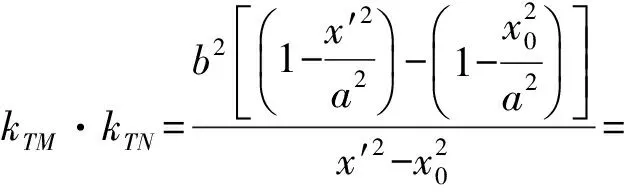
有關(guān)亞黃金橢圓的性質(zhì)遠(yuǎn)遠(yuǎn)不止這些，更多性質(zhì)有待于我們繼續(xù)去挖掘和探究.

[1] 蘇立標(biāo).從一道高考試題談“亞黃金橢圓”的性質(zhì)[J].數(shù)學(xué)教學(xué)研究，2007(6):39-40.

[2] 陳愛花.“黃金”數(shù)列與“黃金”橢圓[J].中學(xué)生數(shù)學(xué)，2006(11):30-31.

[3] 吳文堯.黃金橢圓和黃金雙曲線[J].中學(xué)教研(數(shù)學(xué))，2004(11):27-28.

[4] 魏海濤.橢圓族中的奇葩——黃金橢圓[J].數(shù)學(xué)教學(xué)研究，2008,27(4):35-37.

[5] 阿家斌.優(yōu)美橢圓(雙曲線)的一組性質(zhì)[J].中學(xué)數(shù)學(xué)教學(xué)參考，1997(7):42-43.

[6] 呂林根，許子道.解析幾何[M].北京：高等教育出版社，1987.