2011年高考數學三角函數試題特點分析

●

(嘉興市第一中學 浙江嘉興 314050)

2011年高考數學三角函數試題特點分析

●沈新權鄭俊煒

(嘉興市第一中學 浙江嘉興 314050)

三角函數是描述周期現象的數學模型，在數學和其他學科領域中具有非常廣泛的應用，因此它是高中數學乃至高等數學的重要基礎知識之一．高中新課程標準中的三角函數內容主要包括三角函數的定義、誘導公式、同角三角函數的基本關系、三角函數的圖像和性質、兩角和與差的三角函數、簡單的三角恒等變換以及解三角形等．新課程高考重視對三角函數的圖像和性質的考查，重視對三角函數基礎知識和基本技能的考查．

1 命題特點和知識類型

縱觀2011年全國各省市的數學高考試卷，我們發現2011年對三角函數部分的考查保持了內容、題量、分值的穩定，難度適中．其考查方向主要涉及3個方面：一是三角函數的圖像和性質；二是簡單的恒等變換；三是解三角形問題．解題過程一般是先進行恒等變換，再利用三角函數圖像和性質解題．對能力的考查主要是演繹推理能力、計算能力、綜合應用知識解決問題的能力，體現的數學思想有化歸轉化思想、分類討論思想、函數思想等．

1.1 三角函數的圖像和性質

三角函數的圖像與性質是高考重點考查的內容之一，從2011年各省市的高考數學試卷來看，選擇題、填空題、解答題都有對三角函數的圖像和性質的考查，試題難度中等或中等偏易．

(1)三角函數的概念及同角三角函數的基本關系.

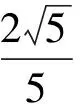
(2011年江西省數學高考文科試題)

分析本題重點考查三角函數的定義．由正弦函數的定義得

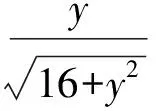
從而y<0，解得y=-8．

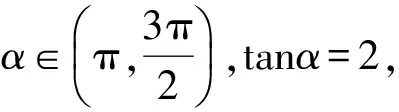
(2011年全國數學高考大綱卷文科試題)

分析本題考查同角三角函數的基本關系．由

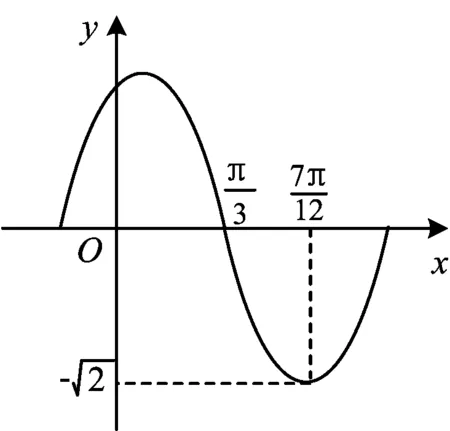
圖1

且

解得

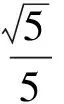
(2)三角函數的圖像.

例3函數f(x)=Asin(ωx+φ)(A,ω,φ是常數，A>0,ω>0)的部分圖像如圖1所示，則f(0)=________．

(2011年江蘇省數學高考試題)

分析本題主要考查由y=Asin(ωx+φ)的圖像寫出其解析式，以及誘導公式和數形結合思想．

由圖像可知

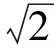
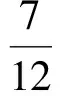
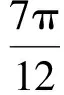
得

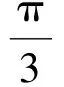
因此

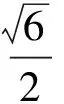
類似的問題還有2011年遼寧省數學高考試題理科第16題、文科第12題．

(3)三角函數的性質.

( )

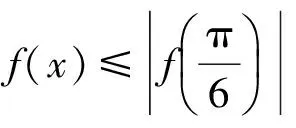
(2011年安徽省數學高考理科試題)

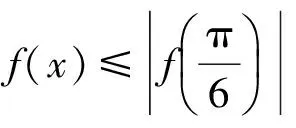
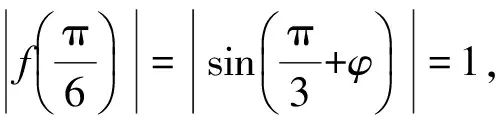
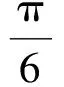
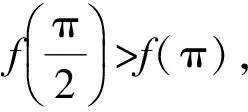
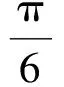
從而

( )

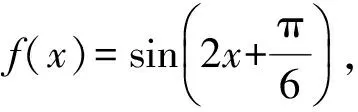
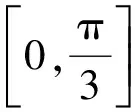
(2011年山東省數學高考理科試題)

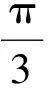
1.2 簡單的三角恒等變換

三角恒等變換是解決三角函數問題的重要工具，2011年的數學高考試卷中主要考查利用三角恒等變換來求值、證明或者求解三角函數的性質問題．

( )

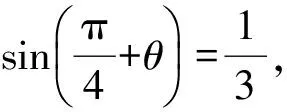
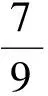
(2011年遼寧省數學高考理科試題)

分析本題是簡單的三角函數求值問題，可以通過兩角和的正弦公式得到sinθ+cosθ的值，再平方求出sin2θ的值；也可以利用誘導公式，再結合二倍角的余弦公式求出sin2θ的值，即

這樣的三角函數恒等變化問題在2011年各省市的數學高考試卷中屢見不鮮，如2011年江蘇省數學高考試題第7題也有類似的做法．

例7已知函數

(1)求f(x)的最小正周期和最小值；

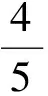
(2011年四川省數學高考理科試題)

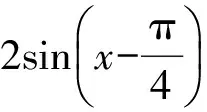
1.3 解三角形

2011年的數學高考重視對解三角形知識的考查，其考查特點是綜合三角函數知識考查正弦、余弦定理在解三角形、三角恒等變換以及實際問題中的應用．

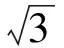
(2011年全國新課標數學高考理科試題)

分析本題主要考查了解三角形與三角函數問題.需要從正弦定理、三角恒等變換、三角函數的性質這3個方面入手．由正弦定理得

AB+2BC=2sinC+4sin(120°-C)=

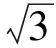
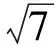
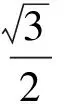
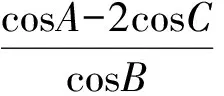
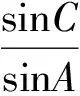
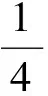
(2011年山東省數學高考理科試題)

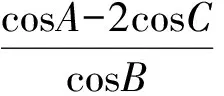
2 亮點掃描

2.1 新穎問題隨處可見

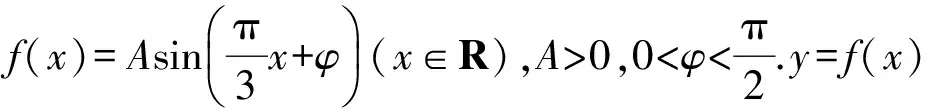
(1)求f(x)的最小正周期及φ的值；

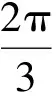
(2011年浙江省數學高考文科試題)

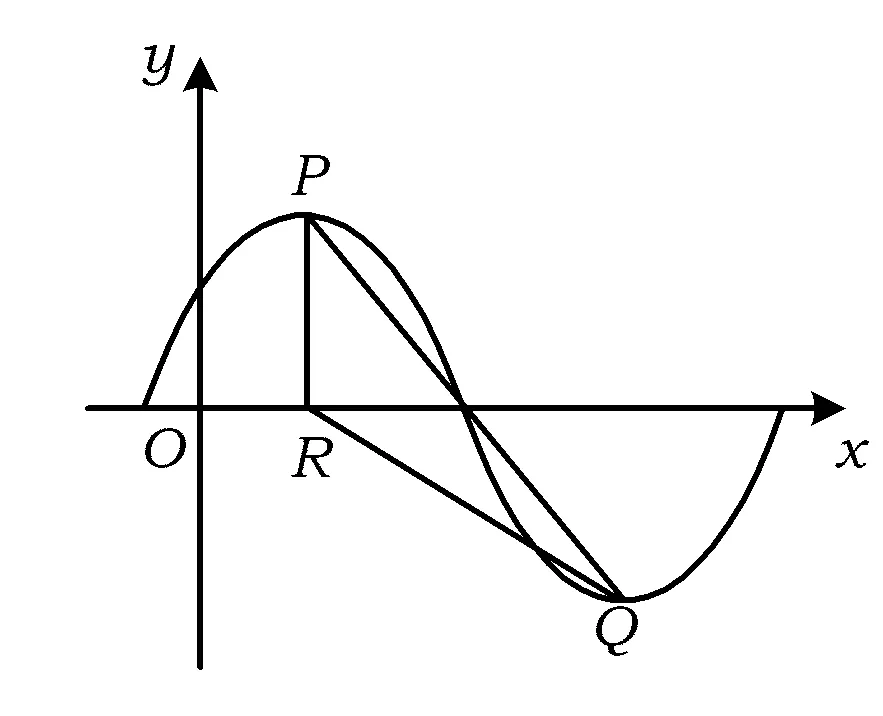
圖2

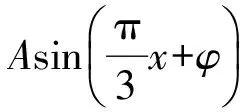
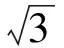
2.2 數學思想之花處處開放

( )

A．沒有零點

B.有且僅有1個零點

C.有且僅有2個零點

D.有無窮多個零點

(2011年陜西省數學高考理科試題)

分析本題可以根據函數的性質(值域、單調性等)進行判斷，但其解法較煩.如果利用數形結合的思想方法進行判斷，則結論直觀、清晰．以三角函數的知識為載體考查學生的數形結合思想、化歸轉化思想、函數方程思想等是2011年數學高考的又一亮點．

2.3 知識交匯時隱時現

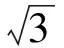
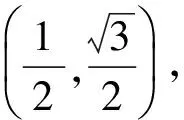
(2)若點P(x，y)為平面區域{x+y≥1,x≤1,y≤1}上的一個動點，試確定角θ的取值范圍，并求函數f(θ)的最小值和最大值．

(2011年福建省數學高考文科試題)

分析本題在三角函數與線性規劃的知識交匯處命題，給人以耳目一新的感覺.問題的求解并不復雜，但對考生知識的全面性和完整性則有較高的要求．

3 復習建議

由于高考中對三角函數內容的考查難度以中等或中等偏易為主，但對大部分數學基礎不太理想的學生來講，三角函數公式多，解題頭緒雜，因此在復習中為了提高學生三角函數的解題能力，可以采取“智取為主，強攻為輔”的復習教學策略.

3.1 重視三角函數公式的復習，展示三角函數公式的內在聯系

三角函數中的公式是進行三角計算的基礎，也是三角變換的基本工具．2011年陜西省數學高考的文、理科試題都考查了余弦定理的證明，由此可見命題教師的良苦用心．三角公式雖然多，但它們之間都有一定的內在關系，譬如誘導公式的主要功能是把任意角的三角函數轉化為銳角三角函數，具有“奇變偶不變，符號看象限”的內在聯系；又如在兩角和與差的三角函數中，兩角和或差的余弦公式是所有這些公式的“母公式”，兩角和與差的其他公式、倍角公式等都可以由它們推導出來．因此，在復習過程中我們要教會學生理清公式之間的關系，在理解的基礎上熟悉、記憶公式，注重公式的變形和逆用，把公式歸類、條理化、系統化．

3.2 關注三角函數解題規律的總結，突破三角函數問題解決的瓶頸

在現行的課程標準中，三角函數問題雖然難度不高，但由于三角公式多、問題變化多的特點，不少基礎差的學生把三角函數視為“攔路虎”.為了解決這一問題，在復習過程中除了重視對三角函數公式的復習以外，還應該要關注學生對三角函數解題過程的規律總結．例如對于化簡與求值題，常用的方法有：角的配湊、平方降次、切化弦、誘導公式、同角三角函數的基本關系引路、利用輔助角公式等轉化為同名三角函數的函數，其主要目的是將未知角變換為已知角進行求解；與三角函數的性質有關的問題，要有目標意識，合理運用基本公式，把三角函數式轉化為一個角的一種三角函數的形式，其間常用的方法有：圖像變換、整體代換等；對于解三角形問題，借助正、余弦定理進行邊、角互化，結合題目條件把邊轉化為角或把角轉化為邊．

3.3 強化數學思想方法的教學，培養學生整體的數學思維

在三角函數的教學和復習中，要引導學生用函數的觀點來理解三角函數，強調角度與函數值的對應關系，引導學生時刻抓住角度、象限、符號三者之間的關系，時刻把三角函數中的內容同函數中的相關內容作對比.同時要讓學生了解，三角函數作為函數，它的一個基本性質就是周期性，這是三角函數不同于其他函數的最基本的東西．另外，整個三角函數都是在直角坐標系下學習的，這也充分體現了解析幾何思想，而解析幾何的最基本特征就是數形結合．因此，數形結合給三角函數增添了形象性、直觀性，也能夠提高學生學習三角函數的興趣和積極性．除此之外，數學中常見的數學思想如轉化與化歸(角與角的轉化、角與邊的轉化、函數名稱之間的轉化等)、函數與方程的思想、換元的思想、整體的思想等在三角函數的教學內容中都有淋漓盡致地體現．在復習中，借助三角函數這一教學內容，強化數學思想方法的教學，才能使得學生在整體上把握住三角函數，使得學生在更高的高度上理解、掌握三角函數，從而提高教學，提高復習實效．