外匯結構性存款的價值分解與定價方法分析

劉鳳琴,張 強

(1.浙江財經學院信息學院,浙江 杭州 310018;2.浙江財經學院金融學院,浙江 杭州 310018)

一、引 言

外匯結構性存款在外匯資產保值增值、銀行發展創新中間業務等方面具有重要的作用,近年來在我國發展速度非常迅猛。但是,隨著美國次貸危機的爆發,許多外匯結構性存款因其聯動貨幣利率的不利變化,不但難以實現預期收益,而且由于匯率變動而可能導致本金的損失。同時,與國外銀行相比,我國銀行在外匯結構性存款業務中往往是作為經銷商的角色出現,即便是自行開發的產品也大都雷同,在未來的競爭中必將處于劣勢處境[1]。因此,研究外匯結構性存款的內在價值構成、定價技術對于我國商業銀行在結構性產品的開發和風險管理等方面具有重要的理論與實際意義。

根據當前銀行所發行的外匯結構性存款的合約條款,其最全面的價值構成可以表述為:外匯結構性存款價值=本金+固定收益價值+浮動收益價值+可贖回權-可回售權[2]。在目前應用的各種外匯結構性存款中,有些相對簡單,僅僅包含其中的一個條款;有些則相對復雜,包含了上述公式中所有條款。本文在此基于以下兩方面考慮,選取帶有提前贖回或回售特征的范圍累積外匯結構性存款作為研究對象,分析探討外匯結構性存款的價值結構及基本定價方法框架。從理論方面來講,該結構性存款包含了影響外匯結構性存款定價的全部三個基本要素;所以,選擇對該產品定價可以完整地分析出各個因素對于產品價值構成的影響,具有重要典型的理論意義。從實際方面考慮,基于增加盈利空間的需要,產品設計者往往偏好于設計出一些結構比較復雜的結構性存款,而當前市場上出現越來越多具有可提前贖回或是回售特征并帶有奇異期權結構性存款也證明了這一點;與此同時,從與Libor利率聯動的角度可以得出,對此產品的定價進行分析也有助于確定我國Shibor利率服從何種隨機過程以及以Shibor利率聯動的人民幣結構性存款定價的研究具有重要的實踐意義[3]。

二、外匯結構性存款的價值構成分解

(一)普通歐式外匯結構性存款的價值構成分析

假設該外匯結構性存款的存續期為 [T0,Tm],其中T0為當前日期,Tm則為該產品的到期日。此外,我們考慮一個完整的概率空間 [Ω,F,Ω],其中,Ω為非空集合,代表了所有可能發生的經濟事件和信息。F作為Ω的子集族被稱為σ-代數,其代表相應時刻所得到的經濟信息,Q代表了相應的概率測度,則不包含提前贖回特征的產品價值可表示為:

其中,VNC(Tj)代表Tj時刻不可提前贖回條件下的外匯結構性存款的理論價值,K(Ti)表示該產品的每個利息支付點發行者向投資者支付的利息,根據結構性產品衍生產品特征,此處利息恰恰是產品設計者偏好的創新之處,因為,該處利息支付可以看做是產品內含衍生工具的盈虧收益函數。以本文定價產品為例,該利息即為各固定期限內范圍累積期權在相應利息支付點的盈虧收益。同時,本文設定當滿足i>m時,(…) =0。因此,VNC(Tm) =1/B(Tm)。

(二)具備提前贖回特征的價值構成

假設該產品具有提前贖回特征時,根據以上分析,其理論價值可以表示為[4]:

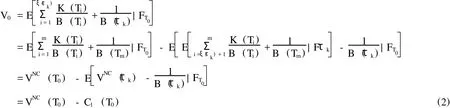
其中,ξ(τ)表示該產品各個停時的順序。因此,具有可提前贖回特征的外匯結構性存款主要有三部分組成:零息債券、由范圍累積期權所得到的浮動收益以及可提前贖回權。其中,VNC(T0)表示零息債券與范圍累積期權的價值之和,C1(T0)代表可提前贖回權的價值。

從發行者銀行追求利潤最大化的角度來講,肯定希望未來所需支付的現金流越少越好,即V值越小越好。同時,VNC(T0)可以看做一個普通的附息債券,其理論價值主要取決于未來標的資產價格的走勢。所以,如何選擇最優執行點以達到V值最小化,主要是通過可提前贖回價值C1(T0)的最小化所決定。可提前贖回期權是一種具有有限個執行點的百慕大式看漲期權,其盈虧函數可以表示為以τk時刻為起始日的不可提前贖回債券的價值與τk時刻產品面值的現值之差[5]。此處,可以把VNC(τk)看做資產價格,而把1/B(Tτk)看做該期權的執行價格。為了計算該期權價值,首先定義該提前贖回期權的盈虧收益函數Z(Tj),即

從上述公式可以看出,如果該期權持有者執行該期權,那么相當于該持有者收到了附息債券所產生的現金流現值,同時支付面值的現值。于是,本文引入一個Snell envelope(U(Tj))j=k…m來代替該期權盈虧函數過程 (Z(Tj))j=k…m。同時,為了理論完整性及實際經常出現產品開始幾期內不允許執行該期權現象,令k表示產品允許提前贖回的起始點,則 (U(Tj))j=k…m具有以下公式:

上式是一個最優停時問題,可以運用向后動態規劃方法進行求解。首先,在產品到期日Snell envelope(U(Tj))j=k…m為零,也就是說,在產品到期日,期權沒有價值。在產品可開始執行點到產品到期日 [Tk,Tm)的這段時間內,該提前贖回價值為持有價值Γ (Tj) =E[U(Tj+1)|FTj]和執行價值Z(Tj)兩者之間的最大值。公式表達即為:

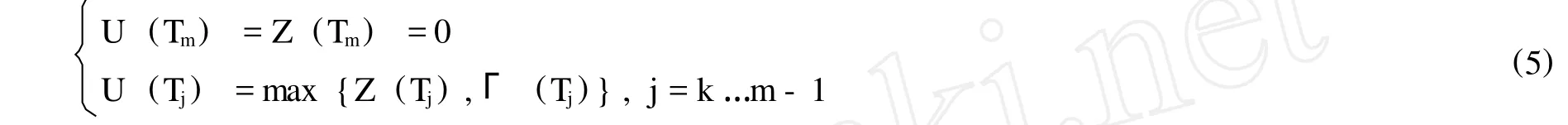
所以,在T0時刻,該提前贖回權的價值為:

其中,第一個等號是從Snell envelope U(Tk)來解釋的,而第一個等號則是從最優停時處產品貼現值的角度來解釋的。因此,具有可提前贖回特征的外匯結構性存款的價值為以奇異期權盈虧函數利息支付的附息債券與可提前贖回權價值之差額,即:

(三)具有提前回售特征的外匯結構性存款價值構成分解

上節主要是從銀行的角度來進行分析的,同理對于投資者能夠單方面終止外匯結構性存款合同的權利則被稱為可提前贖回權,這部分針對該類外匯結構性存款價值構成進行分析。

從投資者追求利潤最大化角度,肯定希望未來所得現金流越大越好,那么具有以下公式[6]:

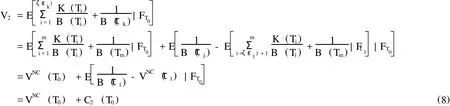
如果希望產品未來產生現金流越大越好,那么就必須使V越大越好。同時,VNC(T0)可以看做一個普通附息債券,其理論價值主要取決于未來標的資產價格走勢。所以,如何選擇最優執行點使V2值達到最大化,主要通過可提前回售價值C2(T0)所決定。可提前回售期權是一種具有有限個執行點百慕大看跌期權,其盈虧函數可以表示為以τl時刻產品面值現值與τl時刻為起始日的普通債券價值之差。此處,可把1/B(Tτl)看做該期權執行價格而把VNC(τl)看作資產價格。為計算該期權價值,首先定義該提前回售期權盈虧收益函數:

從上述公式可以看出,如果該期權持有者執行該期權,那么相當于該持有者收到產品面值的現值,同時支付普通附息債券所產生的現金流現值[7]。于是本文引入一個Snell envelope(U(Tj))j=k…m來代替該期權盈虧函數過程 (Z(Tj))j=k…m。同時,為了理論完整性以及實際過程中經常出現產品開始幾期內不允許執行該期權現象,令k表示產品允許提前回售的起始點,則 (U(Tj))j=l…m具有以下公式:

上式是一個最優停時問題,可以運用向后動態規劃方法進行求解。首先,在產品到期日Snell envelope(U(Tj))j=l…m為零。在產品可開始執行點到到期日 [Tl,Tm)內,該提前回售價值為持有價值Γ (Tj) =E[U(Tj+1)|FTj]和執行價值Z(Tj)兩者之間的最大值,公式為:

所以,在T0時刻,該提前回售權的價值為:

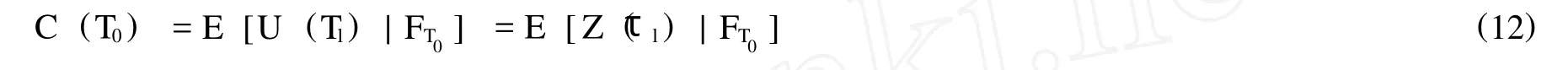
其中,第一個等號是從Snell envelope U(Tl)來解釋的,而第一個等號則是從最優停時處產品貼現值的角度來解釋的。因此,具有可提前回售特征的外匯結構性存款的價值為以奇異期權盈虧函數利息支付的附息債券與可提前回售權價值之和,即:

(四)具有可提前贖回和回售特征的混合外匯結構性存款價值構成分解

上述兩部分主要從產品發行者和投資者兩個角度討論了帶有提前贖回或是回售特征外匯結構性存款價值構成。但從實際情況來講,產品設計者往往偏好于同時帶有可提前贖回和回售特征。所以,這部分針對同時帶有以上兩個特征的產品進行闡述說明。在上述兩種產品定價分析基礎之上,具有可提前贖回和回售特征的混合外匯結構性存款價值為:外匯結構性存款價值=零息債券+浮動收益+可提前贖回價值-可提前回售價值。利用公式表示即為:

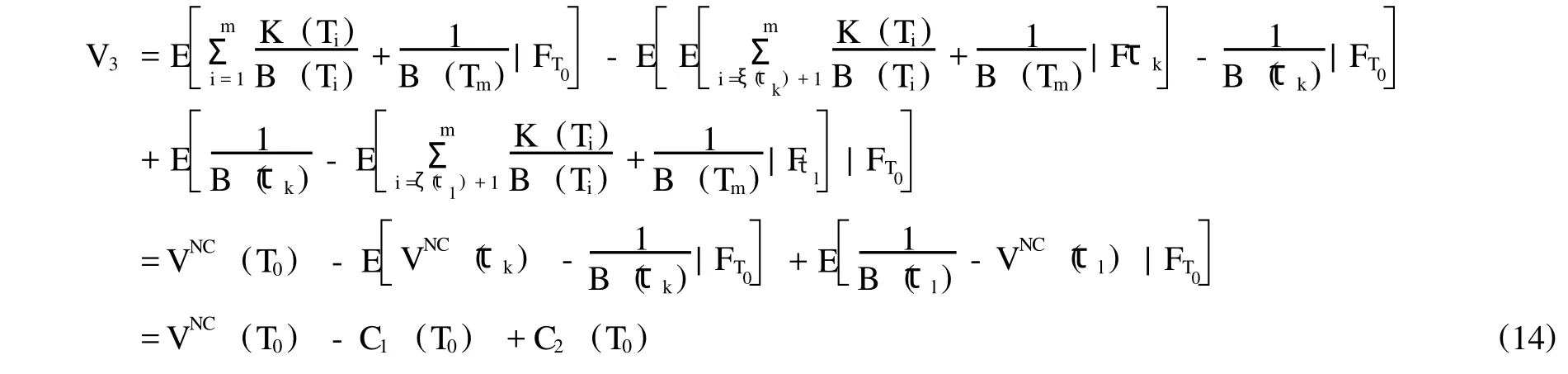
其中,VNC(T0)、C1(T0)以及C2(T0)分析與前面相同。基于以上分析,范圍累積外匯結構性存款本質上是一個利率衍生產品的組合。當討論其定價問題時,主要按照上述所闡述的方法將產品進行價值構成分解,然后將各個組成部分的價值進行加總。

三、附息債券部分的定價理論與方法

根據理論分析,該產品價值構成中的附息債券價值主要由零息債券部分與浮動收益所決定,其中,各期浮動收益即是相應期間內范圍累計期權的盈虧函數[8]。

(一)零息債券部分

外匯結構性存款中具有零息債券特征的組成部分定價方法與普通零息債券定價原理相似。因此,該部分理論價值表現為該產品面值的現值。但是需要強調的是,進行面值貼現時,貼現率如何確定。基于風險中性定價原理,一般簡單處理方法主要是設定其為國債利率,并假設其在短期內不變。但是,由于該類外匯結構性存款的期限基本都在一年以上,單純假設貼現率不變不符合實際情況。所以,需要用一定的利率模型來模擬貼現率的變動[9]。由于該類產品聯動標的變量常常為3個月美元Libor利率,而且數據獲取比較方便。所以,本文采用3個月美元Libor利率作為該零息債券部分的貼現率,其價值可以表示為:

其中,Fi(Ti-1)表示在 [Ti-1,Ti]區間內,以Ti-1為期初時刻的遠期利率,Δ為時間區間的長度,即為Ti與Ti-1之差。

(二)浮動收益部分

該外匯結構性存款的浮動收益部分即為范圍累積期權的盈虧函數,所以,對該部分進行定價的基礎就是需要對范圍累積期權的組成部分——數值期權的價值進行確定[10]。然后根據產品結構原理,將一段期限內的所有數值期權價值加總即可得到該產品浮動收益部分的價值。目前,運用于金融衍生產品定價過程中的數值分析方法主要有網格分析技術和蒙特卡羅模擬方法。蒙特卡羅模擬方法能夠解決以上網格分析方法的不足,從而成為該類期權各種定價方法中最為有效的數值計算方法[11]。首先,蒙特卡羅模擬通過輸入假定條件以及數千次反復模擬得到數千條模擬路徑,在相應的測度下,范圍累積期權的價值即為各條路徑下盈虧函數的平均值。這種定價方法比起網格方法和解析方法都要簡單方便。其次,蒙特卡羅模擬方法與期權標的資產維數獨立,能夠解決網格分析方法中容易出現的“維數災難”問題。最后,隨著蒙特卡羅模擬次數的增加,該期權價值將會趨向收斂到一個穩定的值,可以避免網格定價方法結果的發散性問題。基于以上分析,擬采用蒙特卡羅模擬方法對該外匯結構性存款的浮動收益部分即范圍累積期權進行定價分析。

四、可提前贖回權和可提前回售權部分的適應性定價方法

(一)結構性存款中期權價值構成分析

根據上述價值構成分析,該外匯結構性存款所內含的可提前贖回權和可提前回售權可以分別歸類為可變執行價格的百慕大式看漲期權和看跌期權。由于蒙特卡羅模擬方法的前向性,一度不能將該方法運用到百慕大式期權定價過程中去。一些學者提出了多種美式衍生產品蒙特卡羅定價方法,如隨機樹方法、狀態分層方法、隨機網格方法、策略迭代法和基于回歸的逆向推導方法,而基于回歸的逆向推導方法事實上是廣義上隨機網格方法的一種特殊情況,理論上講其應用性更為普遍,計算量與其他方法相比也減少很多。所以,本文認為基于回歸的逆向推導方法是解決兩個百慕大式衍生證券價值的合理手段。

根據上述分析,該類期權的價值迭代表達式可以用以下公式表達:

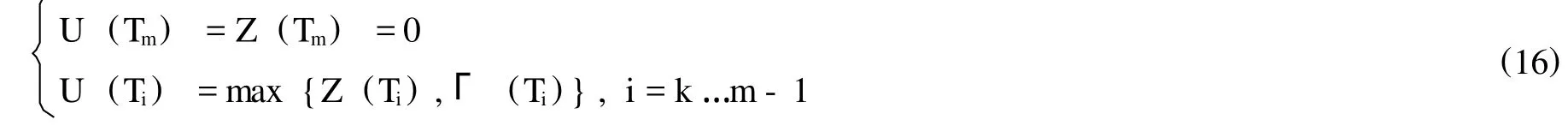
其中,U(Ti)為Ti時刻該類期權的價值函數,Z(Ti)為Ti時刻該類期權的盈虧函數,即執行價值,Γi為Ti時刻該類期權的持有價值。

(二)持有價值計算的一般過程分析

根據回歸計算方法,確定該期權持有價值的公式為:

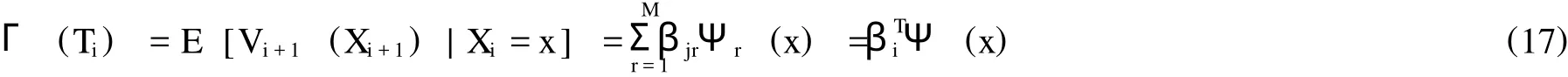
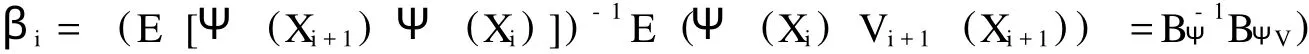
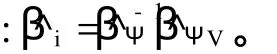
其中,^βΨ和^βΨV實際上是在BΨ和BΨV中選取了有限個元素而組成的向量。所以,當已知一對連續點 (Xij,Xi+1,j的情況下,

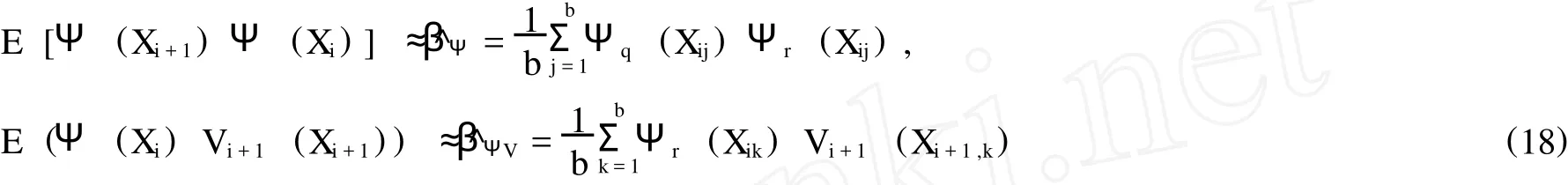
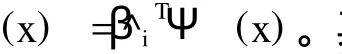
(三)持有價值的價值函數逆向迭代方法及最小二乘蒙特卡羅模擬

1.價值函數逆向迭代方法

在此,利用標的資產所服從的具有馬爾可夫性質,模擬出b條獨立的資產價格變動路徑 {X1j, X2j,…,Xmj},j=1,2,…,b表示路徑條數,而m表示該百慕大式衍生證券在相應路徑所能夠執行的時間點。根據該方法逆向推導特征,該方法步驟為[12]:

最后,按照上述計算方法,在每一條路徑上,都從m-1一直逆推到第一個可執行點,然后將各條路徑的最后值加總求平均,即可得到該衍生證券理論價值:

2.最小二乘蒙特卡羅方法 (LSM)

在此,利用標的資產所服從的具有馬爾可夫性質的隨機過程,模擬出b條獨立的資產價格變動路徑 {Xij,X2j,…,Xmj},j=1,2,…,b表示路徑條數,而m表示該百慕大式衍生證券在相應路徑所能夠執行的時間點。根據該方法的逆向推導特征:

首先計算最后執行點的期權價值函數。由于該產品在最后一期必定執行,所以,該時間點處的期權持有價值為零,那么,其執行價值就等于期權價值函數,即^Vmj=Zm(Xmj),j=1,2,…,b。

最后,按照上述計算方法,在每一條路徑上,都從m-1一直逆推到第一個可執行點,然后將各條路徑的最后值加總求平均,即可得到該衍生證券理論價值:

3.兩種方法比較分析

首先,從回歸計算中所選用的因變量的角度,價值函數逆向迭代方法在運用回歸方法計算回歸系數時所使用的因變量是^Vij=^Ci(Xij),相反,LSM方法使用的因變量是^Vij=^Vi+1,j。

其次,從任意可執行時點處的價值函數的角度,價值函數逆向迭代方法選擇執行價值與回歸方程所得的價值之間的最大值作為該可執行點的價值函數;相反,LSM方法在執行價值與回歸方程所得價值比較中,如果該回歸值大于執行價值,期權不會執行,則選擇以該時刻點為百慕大式期權起始時刻的最優執行時點處執行價值的貼現值作為該執行點的價值函數。

第三,從判斷執行點角度,價值函數逆向迭代方法主要是從最后點開始,從后往前一次判斷,最后求出期初可執行點的衍生證券價值。相反,最小二乘蒙特卡羅方法認為,如果在某個執行點處該衍生證券的執行價值為負,那么,執行者將不會在此時間點提前執行該期權。如果執行價值為正數,則繼續按照上述方法進行比較計算。

最后,從兩種方法的定價效果角度,價值函數逆向迭代方法所得結果與真實值相比為上偏,即,當i→∞時,^Ci(Xij)是Ci(Xij)的無偏估計量,即:E[^Ci(Xij)|Xij]=Ci(Xij)。兩邊取期望值,再根據Jensen不等式,即使假設其持有價值估計值^Ci(Xij)為相應真實值Ci(Xij)的無偏估計,但是該方法所得到最終定價結果^Vij還是大于該類期權真實價值Vij,即所得結果為上偏。相反,LSM定價結果與真實值為下偏,即:^Vi,j=Zi,j1{Zij≥^Cij}+Vi+1,j1{Zij<^Cij}。兩邊取期望可知,LSM方法所得的最終定價結果大于該類期權的真實價值,那么理論價格將低于其真實價格。

4.兩種方法結合的改進模式設想

根據上述分析,兩種方法單獨使用都未能得出一個較為準確的定價結果,所以有必要對其方法進行改進。所以,本文將設想采用以下方法對百慕大式衍生證券進行定價:首先,基于LSM方法的下偏性,利用該方法的逼近法則,我們將在有限模擬數量的情況下,選擇該方法的計算結果實現最大值的基本函數類型和數量。在此基礎之上,將上述結果運用到價值函數逆向迭代算法中去,最終實現最優定價結果。

五、結束語

本文主要根據金融工程分解組合原理,首先分析了影響外匯結構性存款價值的三個基本因素;其次,確定本文所研究的外匯結構性存款理論與實際原因,提出該產品價值的代數解析公式;最后基于該產品各個部分的性質特點對相應的定價理論方法進行闡述,通過系統的論證,得出以下結論:

(1)選擇具有可提前贖回或回售特征的外匯結構性存款為研究對象,在理論上具有典型意義。同時,該產品的定價過程在研究我國Shibor利率服從何種隨機過程,以及以Shibor利率聯動的人民幣結構性存款定價分析具有重要的實踐意義。

(2)基于解析分析方法的復雜性以及網格技術方法由于多變量和多執行點而導致的“維數災難”問題,本文利用蒙特卡羅模擬方法計算外匯結構性存款的附息債券部分的價值。

(3)基于價值函數逆向迭代方法和最小二乘蒙特卡羅方法定價結果的上偏性和下偏性,本文將兩種方法進行結合,即先由最小二乘蒙特卡羅方法得出最佳基本函數類型數量,然后在上述結果之上利用價值函數逆向迭代方法進行產品定價,來對外匯結構性存款價值構成中的可提前贖回權或是回售權進行定價。

[1]顏忠田.結構型商品評價與分析-以逆浮動利率連結商品與匯率連結商品為例 [D].臺灣政治大學學位論文,2007.

[2]鄭振龍,康朝鋒.中國利率衍生產品定價與保值 [M].北京:北京大學出版社,2006.

[3]張睿.外匯結構性存款的合約設計和定價分析 [M].廈門:廈門大學出版社,2005.

[4]Stefan Burth,Thomas Kraus,Hanspeter Wohlwend.The valuation of structured products:empirical finding for the swissmarket[C].ssrn. 2001.

[5]Line Grinden Quinn.Recommending structured products as investment strategy[D],2009.NHH

[6]Pavel A.Stoimenov,SaschaWilkens.Are structured products fairly Priced?An analysisof the Germanmarket for equity-linked instruments[J], Journal of Banking&Finance,2005.

[7]Sascha Wilkens,Carsten Erner.The pricing of structured Product-an empirical investigation of the Germanmarket[J].ssrn.2003.

[9]Damiano Brigo,Fabio Mercurio.Interest ratemodels:theory and practice[M].Springer,2001.

[10]Vishal Subandh.Do structured products give equity like returns?An empirical analysis in the UKmarket[D].Cranfield University,2007.

[11]Longstaff F.A,E.S Schwartz.Valuing American options by simulation:A simple least-squares approach[J].Review of Financial studies,2001,(14):113-147.

[12]Egloff D.Monte Carlo Algorithms for Optimal stopping and statistical learning[J].Annualsof Applied Probability,2005,(15):1-37.