數(shù)形結合的完美演繹

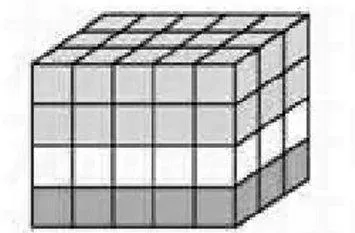
　　北師大版小學數(shù)學教材四年級上冊“乘法結合律和交換律”一課主題圖是一個由許多小正方體搭成的長方體，以前多次教學沒有重視，都忽略掉了。但參與了一位同事的磨課過程后（教學內(nèi)容是“乘法結合律和交換律”），這讓我對這一課的主題圖引起了重視：為什么要在這里安排使用一個大的長方體？教材編寫者的目的是什么？
　　在參與這次磨課過程中，我也認真思考鉆研了教材，細細研究這一長方體，發(fā)現(xiàn)它其實就是乘法結合律和交換律的立體模型，每個面的小正方體個數(shù)體現(xiàn)了乘法交換律，而整個長方體的小正方體個數(shù)體現(xiàn)了乘法結合律和乘法交換律。后來教學中就有意識地充分發(fā)揮長方體的作用，探究乘法結合律和乘法交換律，體現(xiàn)數(shù)與形的完美結合。下面，談談我的體會。
　　第一次教學設計：
　　環(huán)節(jié)一：嘗試，分析與匯報
　　出示42×125×、25×38×4、25×125×8×4三道算式，然后請學生獨立嘗試計算，分析方法，并匯報方法。板書如下：
　　42×125×8=42×（125×8）
　　25×38×4=25×4×38
　　25×125×8×4=（25×4）×（125×8）
　　師：你認為這樣改變可以嗎？為什么可以？
　　環(huán)節(jié)二：揭題，探索與發(fā)現(xiàn)
　　分析42×125×8=42×（125×8），你有什么發(fā)現(xiàn)？（乘數(shù)位置不變，運算順序變了，積不變）
　　師：是否所有的乘法算式都有這樣的規(guī)律呢？（學生舉例略）
　　師：能否用自己的方式表達這種規(guī)律呢？（總結概括乘法結合律的字母公式）
　　環(huán)節(jié)三：探究乘法交換律（過程同第二環(huán)節(jié)）
　　環(huán)節(jié)四：指導學生閱讀教材，熟悉、知道這兩個規(guī)律叫做乘法結合律和乘法交換律，然后師生共同小結規(guī)律特點。
　　乘法結合律：在乘法中，改變運算順序，積不變。
　　乘法交換律：在乘法中，交換因數(shù)位置，積不變。
　　環(huán)節(jié)五：課堂練習（利用發(fā)現(xiàn)的規(guī)律進行計算）
　　按照“嘗試——發(fā)現(xiàn)——舉例——結論——運用”的步驟教學，一切都順理成章、水到渠成，但是細細思考，這樣的教學是建立在學生認識乘法定律的基礎之上，這樣的探究與發(fā)現(xiàn)是在學生已經(jīng)認識到乘法定律客觀存在的前提下進行的。那么，課堂教學中的探究與發(fā)現(xiàn)就變成了舉例和運用，所謂的舉例其實就是迎合、驗證，結論早已定形，運用也是機械應用。如果了解學生的認知起點，就會發(fā)現(xiàn)學生對運算定律的認識是模糊的、不全面的。既然是模糊的，那么怎樣才能通過課堂教學讓學生找到對乘法定律的清晰的認識，建立簡潔的模型？顯然，不能從第一次教學設計中找到答案。仔細分析教材，教材在安排本課的內(nèi)容時，有一個指導思想，就是把乘法結合律的引出作為學生探索活動的題材，所以其活動的名稱叫“探索與發(fā)現(xiàn)”。本活動開展的重點是指導學生探索乘法的結合律，教材呈現(xiàn)探索過程：發(fā)現(xiàn)問題——提出假設——舉例驗證——建立模型。
　　第二次教學設計：
　　環(huán)節(jié)一：發(fā)現(xiàn)問題
　　1．觀察長方體
　　師：這里有幾個小正方體？
　　生：60個。
　　師：你是數(shù)出來的，還是算出來的？（生列算式，師引導學生從不同角度計算正方體的個數(shù)）
　　2．研究算法的異同
　　相同點：都是通過3、4、5這三個數(shù)連乘得來。
　　不同點：先算的部分不同。
　　根據(jù)先算部分的不同得到三個算式：3×4×5、3×（4×5）、（3×5）×4。
　　3．研究算式特征，體會變化
　　不變：數(shù)字，運算符號，結果。
　　變化：運算形式，因數(shù)位置。
　　環(huán)節(jié)二：提出假設（構建研究素材，提出猜想）
　　表示改變運算順序的兩個算式：3×4×5、3×（4×5）。
　　表示改變因數(shù)位置的兩個算式：3×4×5、（3×5）×4。
　　師：這樣的發(fā)現(xiàn)是不是有科學性呢？那么，這個規(guī)律對其他的算式也正確嗎？
　　環(huán)節(jié)三：舉例驗證（學生舉例，反饋）
　　環(huán)節(jié)四：建立模型
　　師：這樣的算式從數(shù)量上能不能舉完？你能否用其他方式表示出來？［揭示乘法結合律：（a×b）×c=a×（b×c）］
　　師：你知道乘法結合律告訴我們什么？
　　環(huán)節(jié)五：回顧方法
　　師：請大家想一想，我們是怎樣發(fā)現(xiàn)乘法結合律的呢？
　　環(huán)節(jié)六：乘法交換律的探究
　　環(huán)節(jié)七：應用深化，完善認識
　　思考：
　　教師根據(jù)教材的編寫意圖，通過組織學生活動，使他們不知不覺地進行數(shù)學規(guī)律的探索。縱觀整個教學流程，有以下幾個特點：
　　1.通過數(shù)正方體，引出乘法算式
　　雖然學生對三個數(shù)相乘的乘法運算是熟悉的，也會計算，但教師在設計時仍讓學生自己數(shù)正方體，這樣做可能要花費一些時間。然而，正是由于經(jīng)歷了自己數(shù)正方體的活動，使學生在后面討論、發(fā)現(xiàn)問題時有了一個直觀的題材，而這個題材既可以使學生借助形象模型進行直觀思考，又可以幫助學習有困難的學生理解算式的意義。
　　2.經(jīng)歷猜想和驗證，概括出乘法的結合律
　　學生發(fā)現(xiàn)不同的算式其結果是相同的——這是在計算小正方體的個數(shù)時的一個十分特殊的情況，因為不同的數(shù)法實際上都是在數(shù)同一個長方體，個數(shù)當然不變。當學生有了這一發(fā)現(xiàn)后，教師問學生“這樣的發(fā)現(xiàn)是不是有科學性呢？那么，這個規(guī)律對其他的算式也正確嗎”，從而引導學生進一步擴大驗證的范圍。經(jīng)歷猜想和驗證對學生來說特別重要。學生通過數(shù)直觀的正方體提出猜想，在學生獲得感性認識的基礎上，教師又啟發(fā)學生用抽象的算式來舉例驗證，從而為發(fā)現(xiàn)、概括乘法結合律奠定了基礎。
　　3.及時梳理思路，掌握探索規(guī)律的基本步驟
　　探索數(shù)學的規(guī)律是有一個過程的，對這個過程的認識并不是教師傳授的，而是需要學生自己體驗、感受的。對學生已有的體驗與感受及時地進行梳理，是提高探索能力的重要一環(huán)。在本案例的最后，當學生已經(jīng)概括出乘法的結合律后，教師并沒有立即組織學生進行相關內(nèi)容的練習，而是詢問學生：“請大家想一想，我們是怎樣發(fā)現(xiàn)乘法結合律的呢？”通過學生對方方面面的反思，引出教師最后的概括。雖然，學生要真正理解教師所做的概括還需要大量的體驗，但相信經(jīng)歷多次這樣的過程，學生就能體會到探索的基本步驟。但是也凸顯其中的弱點：沒有充分發(fā)揮長方體的作用。主要表現(xiàn)在研究素材的三個算式上，3×4×5 、3×（4×5）、（3×5）×4出現(xiàn)的較牽強，出現(xiàn)之后沒有聯(lián)系長方體。如果教師僅僅是為了構建研究素材而把長方體作為素材來源的話，那么就不能很好地發(fā)揮長方體的作用。細細羅列，計算有幾個小正方體一共有12個算式，分三大類。第一類從上面看：3×5×4、5×3×4、4×（3×5）、4×（5×3）；第二類從右側面看：3×4×5、4×3×5、5×（3×4）、5×（4×3）；第三類從正面看： 4×5×3、5×4×3、3×（4×5）、3×（5×4）。這12個算式之間的變化關系有乘法交換律：3×5=5×3、3×4=4×3、4×5=5×4；還有乘法結合律：3×5×4=3×（5×4）、5×3×4=5×（3×4）、3×4×5=3×（4×5）、4×3×5=4×（3×5）、4×5×3=4×（5×3）、5×4×3=5×（4×3）。3×5和5×3都表示上面這一面的小正方體的個數(shù)，每個面的小正方體個數(shù)體現(xiàn)了乘法交換律，而整個長方體的小正方體個數(shù)體現(xiàn)了乘法結合律。我認為沒有哪一種方式能夠像長方體一樣把乘法結合律和乘法交換律體現(xiàn)得這么淋漓盡致，充分體現(xiàn)了數(shù)形結合。
　　如何充分發(fā)揮長方體的作用？我一直在思索，恰恰自己教學四年級上冊，可以親自帶著問題，按照自己的想法進行試教，我覺得非常不錯。主要體現(xiàn)在第一環(huán)節(jié)和第二環(huán)節(jié)的改進上。
　　環(huán)節(jié)一：兩次充分觀察長方體
　　第一次觀察，學生獨立觀察長方體，列出算式，匯報算法。
　　第二次觀察，在學生匯報算法的時候，教師適當引導每個學生從不同角度進行觀察：你也是這樣觀察的嗎？如果不是，那請你也從這一角度進行觀察，你能想出其他算式嗎？得到從一個角度觀察的一組算式，進而得到12個不同的算式，分類有序板書。
　　環(huán)節(jié)二：從算式的數(shù)字本身和意義兩個角度自己發(fā)現(xiàn)乘法結合律與