定時截尾瑞利分布的Bayes估計
王曉紅,欒江輝
(吉林師范大學 數(shù)學學院,吉林 四平 136000)
瑞利分布是一種重要的壽命分布,引起國內(nèi)外許多學者的興趣.關(guān)于瑞利分布可靠性的研究,國內(nèi)外已有一些研究,文[1-2]在Linex損失和對稱熵損失條件下研究了瑞利分布參數(shù)和參數(shù)倒數(shù)的貝葉斯估計,文[3]平方誤差損失函數(shù)和熵損失函數(shù)下討論了Rayleigh分布參數(shù)的Bayes估計的比較問題.在可靠性試驗中,定時截尾是一種重要的試驗形式,但在熵損失函數(shù)下,對瑞利分布參數(shù)的貝葉斯估計的研究還未發(fā)現(xiàn),為此本文研究在定時截尾情形下瑞利分布參數(shù)θ的Bayes估計.
1 參數(shù)θ的Bayes估計
設(shè)產(chǎn)品的壽命X服從瑞利分布,則其分布函數(shù)和概率密度函數(shù)的表達式分別為
F(x)=1-e-θx2,x>0,θ>0,
f(x)=2θxe-θx2,x>0,θ>0.
下面討論熵損失函數(shù)下參數(shù)θ的Bayes估計.
定義1[4]設(shè)隨機變量X服從密度函數(shù)為f(x,θ)的分布,其中θ為參數(shù).如果δ是判決空間中的一個估計,則熵損失函數(shù)為似然比對數(shù)函數(shù)的數(shù)學期望,即
(1)
設(shè)X1,X2,…,Xn是來自分布為F(x)的相互獨立隨機變量序列,在定時截尾下得到的觀察值記為(Y1,δ1),(Y2,δ2),…,(Yn,δn),其中Yi=Xi∧T,T為定時截尾時間,滿足0 (2) 注:(Yi,δi)(i=1,2,…,n)的聯(lián)合密度的控制測度已改變. 將(2)式代入(1)式得 (3) 計算得 Eδi=E(IXi≤T)=F(T)=1-e-θT2 (4) (5) 將(4)、(5)式代入(3)式得 易證,這個損失函數(shù)關(guān)于δ是嚴凸的. 定理1 在定時截尾情形下,損失函數(shù)為熵損失函數(shù)時對于任何先驗分布,瑞利分布參數(shù)θ的Bayes估計為 其中F(x)是瑞利分布的分布函數(shù). 證明 設(shè)δ(Y)是參數(shù)θ的一個估計,則參數(shù)θ的Bayes風險為 令 對該式求導并令導數(shù)為零,得 因為φ(δ(Y))為嚴格凸函數(shù),所以有唯一最小值點,即 是其最小值點.因此參數(shù)θ的Bayes估計的一般形式為 定理2 在定時截尾情形下,損失函數(shù)為熵損失函數(shù)時取參數(shù)θ的先驗分布為Gamma分布Γ(λ,β),則瑞利分布參數(shù)θ的Bayes估計為 證明 參數(shù)θ的先驗分布為Gamma分布Γ(λ,β),則θ的密度函數(shù)為 則聯(lián)合密度函數(shù)為 f(y1,y2,…,yn,δ1,δ2,…,δn)=(2θ)μγe-θρ, 從而θ的后驗密度函數(shù)為 引理1[5]在給定的貝葉斯決策問題中,假如對給定的先驗分布π(θ),θ的Bayes估計δπ(X)是唯一的,則它是容許的. 定理3 在定時截尾情形下,損失函數(shù)為熵損失函數(shù)時對于任何先驗分布,瑞利分布參數(shù)θ的Bayes估計是可容許的. 證明 在定時截尾情形下,損失函數(shù)為熵損失函數(shù)時瑞利分布參數(shù)θ的Bayes估計是唯一的,故由引理1,θ的Bayes估計是容許的. 參考文獻: [1]陳志強,韋程東,韋瑩瑩.Linex損失下Rayleigh分布參數(shù)倒數(shù)的Bayes估計[J].廣西科學,2007,14(4):362-364. [2]任海平.對稱熵損失函數(shù)下Rayleigh分布參數(shù)的Bayes估計[J].江西理工大學學報,2010,31(5):64-66. [3]Soliman A.Ahmed.Comparion of Linex and Quadratic Bayes Estimators for the Rayleigh Distribution[J].Commun Statist.-Theory Meth,2000,29(1):95-107. [4]熊常偉,張德然,張怡.熵損失函數(shù)下幾何分布可靠度的Bayes估計[J].數(shù)理統(tǒng)計與管理,2008,27(1):82-86. [5]茆詩松,王靜龍,濮曉龍.高等數(shù)理統(tǒng)計[M].北京:高等教育出版社,1998.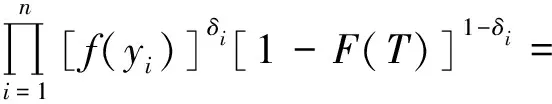
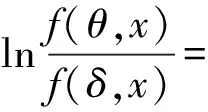
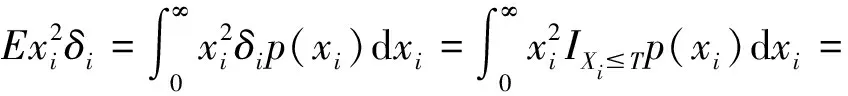
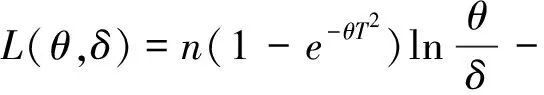

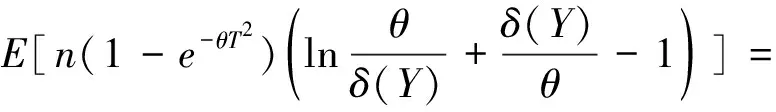
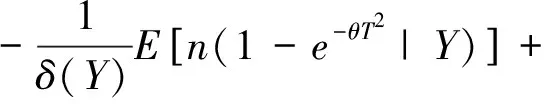
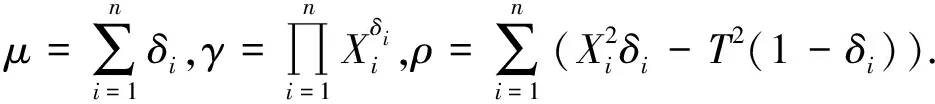
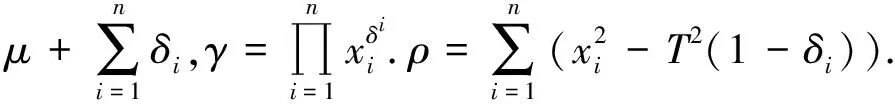
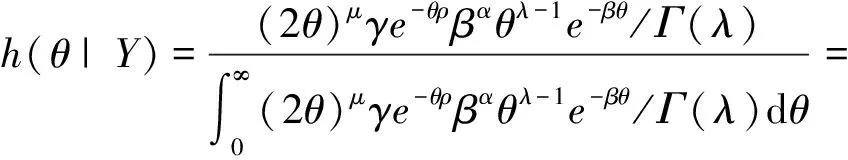
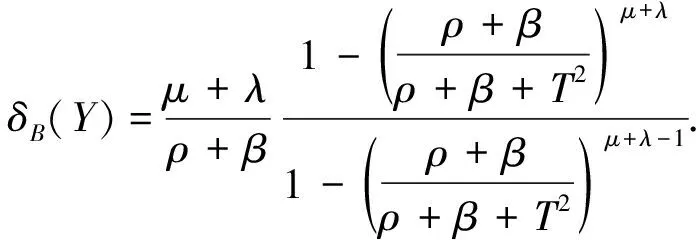
2 參數(shù)θ的Bayes估計的可容許性

