準P波方程緊致交錯網格井間地震波場模擬及邊界條件

孟凡順，張 亮，李景巖，李洋森

（1.中國海洋大學 海洋地球科學學院，山東 青島 266100；2.中國海洋大學 “海底科學與探測技術”教育部重點實驗室，山東 青島 266100；3.中海石油（中國）有限公司 湛江分公司，廣東 湛江 524057）

準P波方程緊致交錯網格井間地震波場模擬及邊界條件

孟凡順1，2，張 亮3，李景巖1，2，李洋森1，2

（1.中國海洋大學 海洋地球科學學院，山東 青島 266100；2.中國海洋大學 “海底科學與探測技術”教育部重點實驗室，山東 青島 266100；3.中海石油（中國）有限公司 湛江分公司，廣東 湛江 524057）

研究井間地震波場的形成過程以及波場的傳播機理、規律，對于指導實際井間地震勘探有著重要的意義。基于具有垂直對稱軸的橫向各向同性（VTI）介質中的一階準P波方程，應用具有無條件穩定性質的緊致交錯網格隱式差分格式求解該方程。重點研究了緊致交錯網格求解該方程的完全匹配層（PML）吸收邊界條件，在此基礎上實現了VTI介質中一階準P波方程的井間地震波場的正演模擬。數值算例表明：緊致交錯網格能精準模擬VTI介質中準P波的傳播過程，得到高精度的正演結果。一階準P波方程能以足夠的精度描述VTI介質中準P波特征。完全匹配層吸收邊界能有效地解決人工邊界問題，是一種高效的邊界吸收算法。

井間地震，緊致交錯網格；VTI介質；準P波方程；完全匹配層

0 前言

井間地震是將震源與檢波器都置于井中進行地震波觀測的一種新的物探方法。該方法可以獲得較高分辨率的地震信號，與地面地震互補可以大幅度地提高復雜陸相儲層的描述精度［1、2］。但是當地下地質比較復雜時，尤其是地質呈現各向異性時，井間地震波場類型多，而且各種類型波之間相互干涉或疊加，形成了非常復雜的井間地震波場，這對于井間地震波場的識別和分離以及成像帶來了很大的麻煩［3］。因此應用正演模擬技術研究復雜地層中井間地震波場特征和傳播規律，具有非常重要的理論和實際意義。

目前，各向異性介質中地震波的正演模擬，主要通過求解彈性波方程實現［4～6］。該方法用三分量矢量場描述地震波場，每個分量都包含縱波和橫波，因此能模擬比較豐富的波場信息。但也具有十分明顯的缺陷［7］，主要表現在：各向異性介質彈性波方程包含多個分量，這就必然導致計算速度慢、效率低，并且這些彈性參數物理意義不明確，在實際生產中這些參數也很難得到。目前在實際生產中仍以縱波勘探為主，即使在各向異性介質中，也仍然只記錄縱波信息。在目前技術的情況下，多分量理論數據的應用受到了限制。為克服以上缺陷，Alkhalifan［8］假設橫波速度為零，推導出各向異性介質中的準P波方程。該方程對彈性波方程能有效的近似，更加有利于研究各向異性介質中準P波的傳播規律。隨后，Hestholm［9］推導了該方程的一階速度～應力方程形式，并采用高階差分實現了該方程的數值模擬。

在數值模擬領域中，由于有限差分法計算效率高，容易解決邊界問題，編程簡單等優點被廣泛地應用。Madariage［10］首次提出了交錯網格有限差分算法，極大地提高了有限差分數值模擬的精度。Lele［11］提出了高階緊致網格有限差分算法，緊致網格是一種隱式差分格式，與顯式差分格式不同的是其具有無條件穩定的性質，其主要優勢在于應用較少的網格節點就可以得到高精度的模擬記錄，而且較容易解決邊界問題［12～14］。Nagarajan［15］應用緊致交錯網格有限差分成功解決了大渦問題。Bendiks［16］應用緊致交錯網格有限差求解了Navier－Stokes方程，結果表明緊致交錯網格有限差分能夠很好地壓制數值頻散。

作者在本文根據VTI介質中的一階準P波方程，研究了該方程在緊致交錯網格中求解的高階有限差分算法。重點研究了緊致交錯網格一階準P波方程的PML邊界方程，在此基礎上實現了VTI介質中準P波方程的正演模擬，得到了高精度的合成記錄。

1 基本原理

1.1 一階準P波方程

二維VTI介質中準P波方程的一階速度～應力方程為［9］：

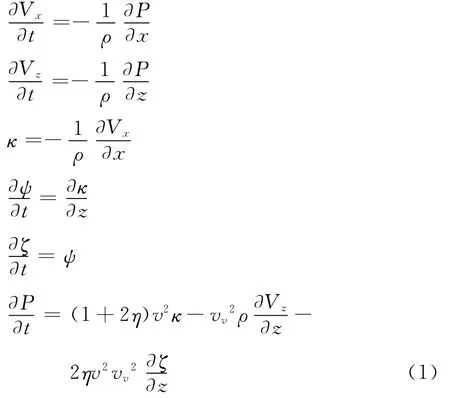
其中 Vx、Vz分別為x、z方向的質點速度；ρ為密度；ψ、κ、ζ為中間變量。

1.2 緊致交錯網格時間差分近似

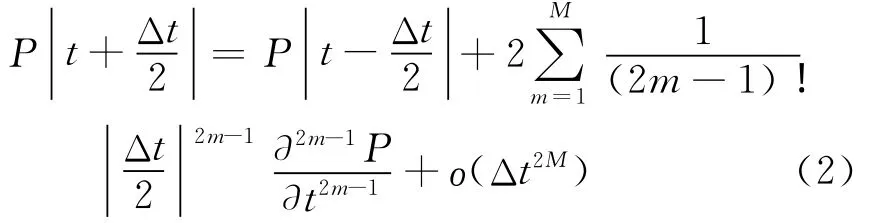
1.3 緊致交錯網格空間差分近似

設f（x）是連續函數，并且存在n階偏導數，令

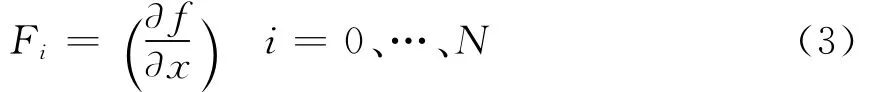
2 N點2 N＋2階緊致交錯網格有限差分格式為［18］式（4）。

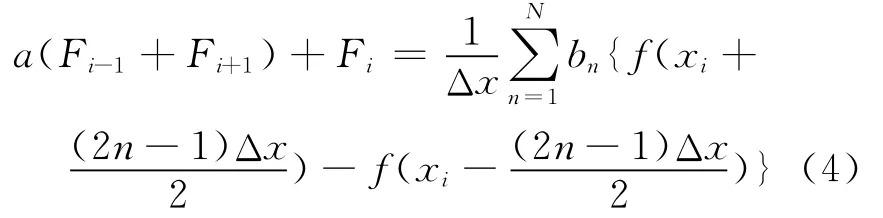
其中 Δx是空間采樣間隔，待定系數a、bn可以通過將處Taylor公式展開后解方程組求得。8點10階緊致交錯網格的待定系數為：a＝0.257 89、b1＝0.889 87、b2＝ 0.216 12、b3＝－0.004 7、b4＝0.000 15。例如，在x方向應力σxx的空間一階差分8點10階近似為：

其中 A和B是n×n階系數矩陣，Fj和fj是n×1階列向量。

向前差分格式：

z方向空間一階差分8點10階近似為：

其中 Fi＝ ［Fi，1Fi，2…Fi，n－1Fi，n］；fi＝ ［fi，1fi，2…fi，n－1fi，n］是1×n維行向量，AT是A 的轉置，向前差分B＝B1，向后差分B＝B2。

1.4 緊致交錯網格差分格式的構造

緊致交錯網格單元的空間交錯策略見下頁圖1，利用公式（5）、公式（6）及網格的空間分布即可得VTI介質中一階準P波方程的緊致交錯網格時間二階，空間8點十階有限差分格式為：

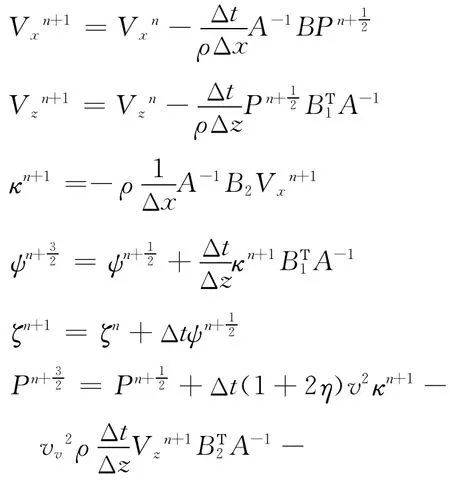
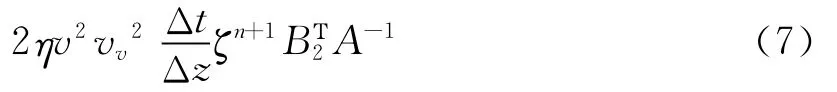
式中 Δx、Δz為空間離散間隔；Δt為時間離散間隔；i、j為空間離散點序號；n為時間離散點序號。

1.5 PML吸收邊界條件

根據PML分裂原理［19］針對二維VTI介質中的一階準P波方程，應用緊致交錯網格有限差分導出了適應該方程的吸收邊界方程，見式（8）～式（16）。

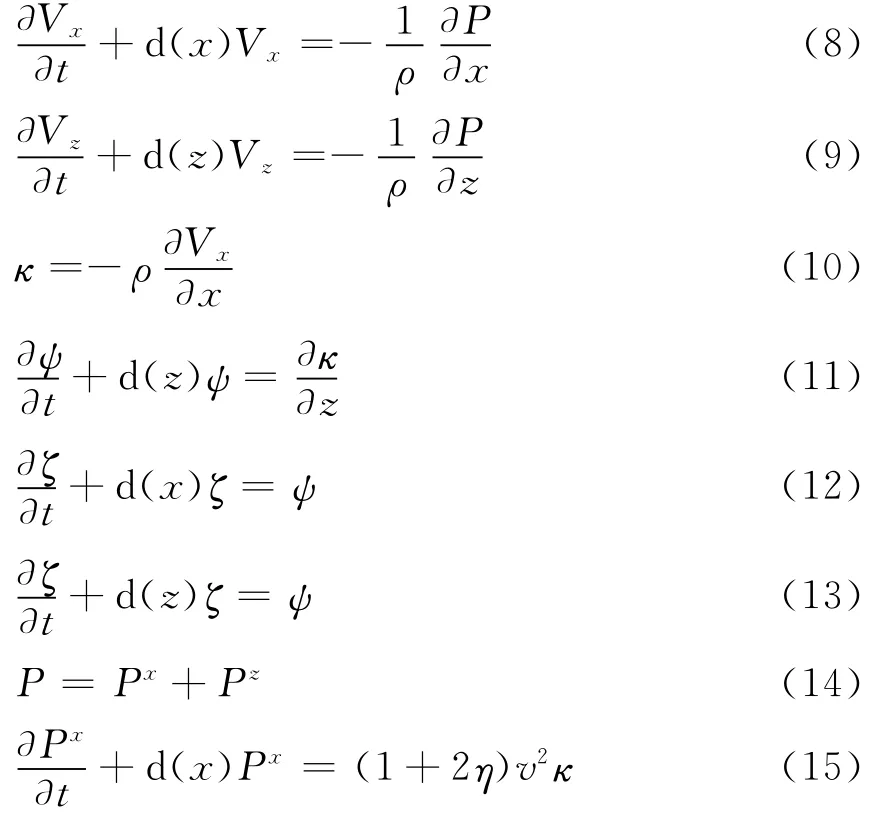
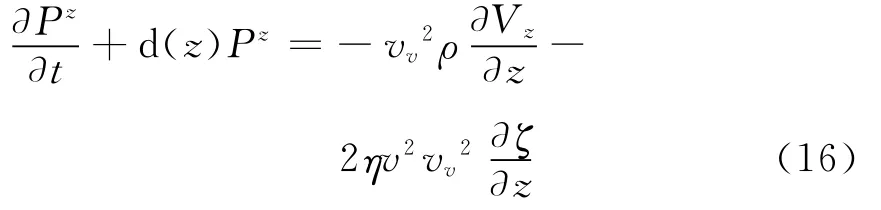
其中 式（12）和式（13）分別對應x方向和z方向，其余各式在x方向和z方向均可使用；Px、Pz分別為P在x方向和z方向上的分量；d（x）、d（z）為x與z方向的吸收因子。

作者以式（14）～式（16）為例給出其時間二階精度，空間8點十階精度的緊致交錯網格有限差分格式，即：

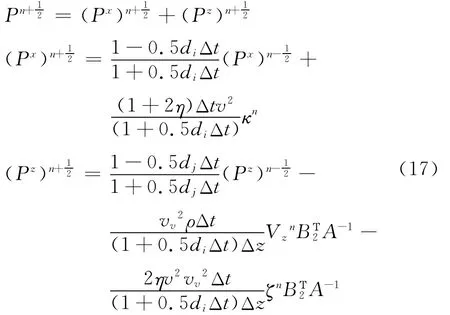
其中 di、dj為x與z方向吸收因子的離散值。

2 數值模擬

2.1 均勻VTI介質模型

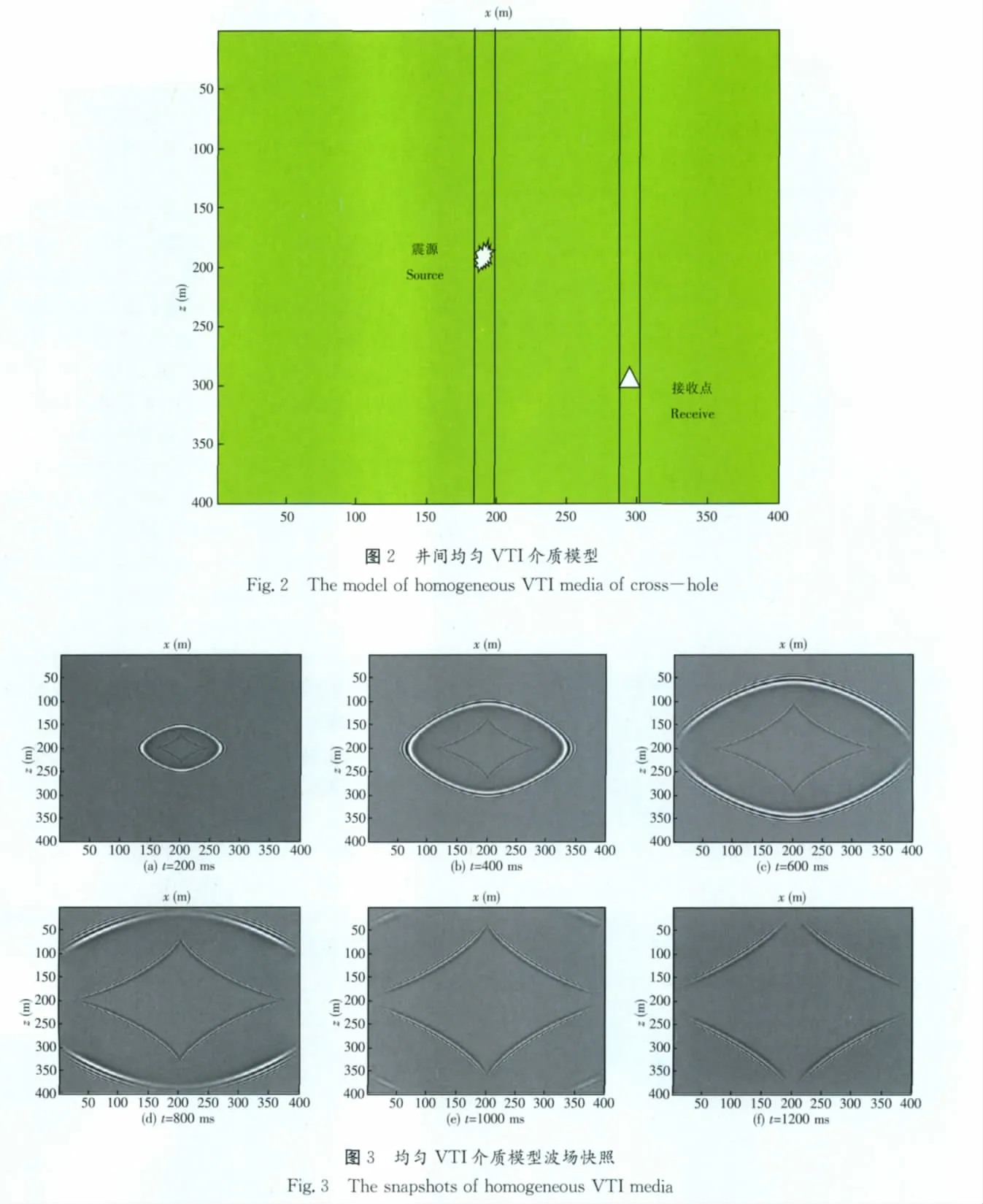
首先設計一個400×400的均勻VTI介質模型，來檢驗緊致交錯網格有限差分數值模擬算法的可行性。合成計算的空間步長和時間步長分別為Δx＝ Δz＝10m，Δt＝1ms，介質參數v ＝2 401m／s、vv＝ 2 450m／s、η ＝ 0.518、ρ ＝2 150kg／m3。震源為主頻30Hz的Ricker子波位于模型的中間，如下頁圖2所示。

采用時間二階精度，空間八點十階精度對上述模型進行模擬，得到的波場快照如圖3所示（見下頁）。波場快照中外層傳播較快的即為準P波，內層呈菱角狀傳播較慢的波即為由計算誤差產生的P2波［20］。

由分析波場快照可以得出：緊致交錯網格隱式格式有限差分模擬的地震記錄數值頻散較小，模擬的效果比較有利于波場的識別、速度分析、偏移成像等。緊致交錯網格隱式格式準P波方程的PML吸收邊界，能有效地吸收人工邊界產生的虛假反射波，而且與內層網格的高階格式相匹配，避免了吸收邊界區與內層網格交界面由于差分階數的突變而產生的偽反射，是一種高效的邊界吸收算法。

為了驗證準P波方程對VTI介質中縱波的近似程度，作者在本文做了如下試驗，震源點位于模型中間，接收點位于震源右下角水平和垂直距離均為1 000m處，其中彈性波方程正演模擬采用的參數和一階準P波方程相一致，可通過計算得出［21］。并且彈性波方程模擬時采用縱波源激發，彈性參數同上。

后面圖4為在相同彈性參數的情況下，分別應用一階準P波方程和彈性波方程得到的理論地震圖，分析地震圖可以得到以下認識：

（1）緊致交錯網格有限差分算法產生的數值頻散很小，主要表現在接收的振動曲線平滑很少出現劇烈抖動。

（2）一階準P波方程在動力學上對VTI介質中的準P波具有很高的近似精度。主要表現在一階準P波方程和彈性波方程在準P波的起跳時間上一致，而且兩種方程得到振動曲線準P波部份重合度很高。

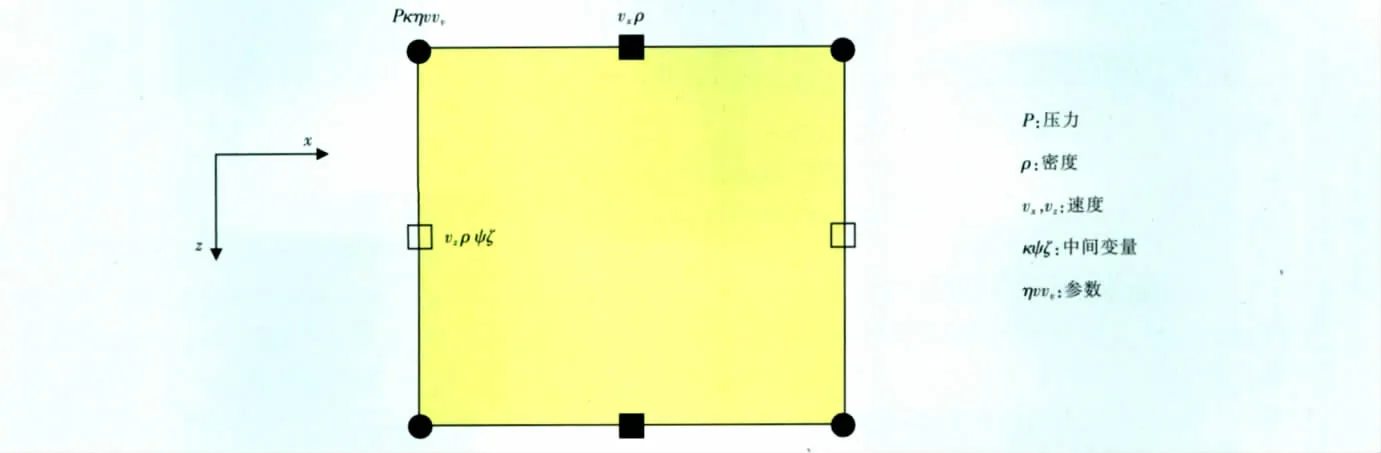
圖1 緊致交錯網格空間單元交錯示意圖Fig.1 Elementary cells of compact staggered grids

（3）彈性波方程模擬時，即使采用縱波源激發VTI介質中也并非只產生qP波，還將產生與qP波耦合的qSV波；準P方程產生與彈性波方程同樣的qP波，還將產生由計算誤差引起的P2波。

2.2 層狀介質模型

模型如圖5所示（見下頁），模型計算區域為400×400，空間采樣間隔Δx＝Δz＝10m，時間采樣間隔Δt＝1ms，激發井和接收井分別位于水平1 500m和2 500m處，井間距1 000m，道間距10m，共400道。記錄時間長度t＝1 500ms，炮點深度為1 200m和2 000m，介質的分界面位于垂直深度1 500m、2 500m處，介質“1”為各向同性介質，介質“2、3”為VTI介質。介質的相關參數見后面表1。其它模擬參數同均勻VTI介質模型。

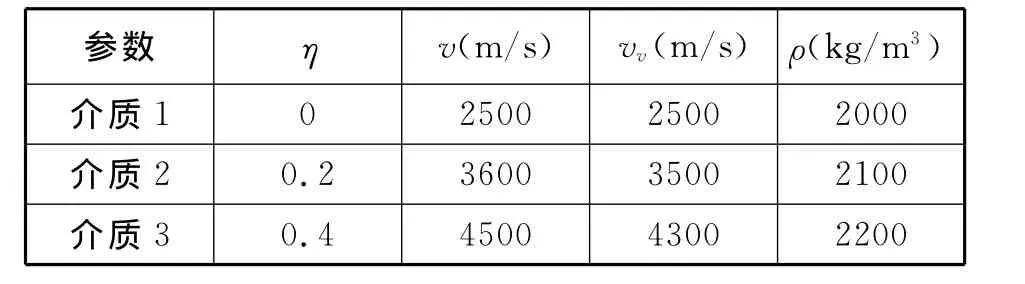
表1 層狀介質模型參數Tab.1 The physical parameters of layer media

通過分析圖6、圖7井間地震層狀介質模型的共炮點道集記錄特征可以得出：

（1）緊致交錯網格有限差分方法能高精度的模擬井間地震波場。各向同性介質中井間地震直達波同向軸為雙曲線，而VTI介質中井間地震直達波的同向軸不再是雙曲線形態。因為當地層表現為各向同性時，地震波傳播的速度在不同方向上為恒定不變的，時距曲線方程為雙曲線方程。當地層表現為VTI介質時，地震波傳播的速度在不同方向上是變化的，此時方程就不是雙曲線方程了，表現在共炮點道集記錄上直達波就不是雙曲線形態。

（2）震源位于各向同性介質中時，只產生縱波向四周傳播，波傳播到模型交界面處將產生透射縱波和反射縱波（見圖6標注），界面處不產生轉換橫波。這是一階準P波方程模擬和彈性波方程模擬井間波場時的主要區別，彈性波方程模擬時將產生各種轉換橫波［22］。對比結果表明，一階準P波方程能夠對VTI介質中準P波進行很好的近似。

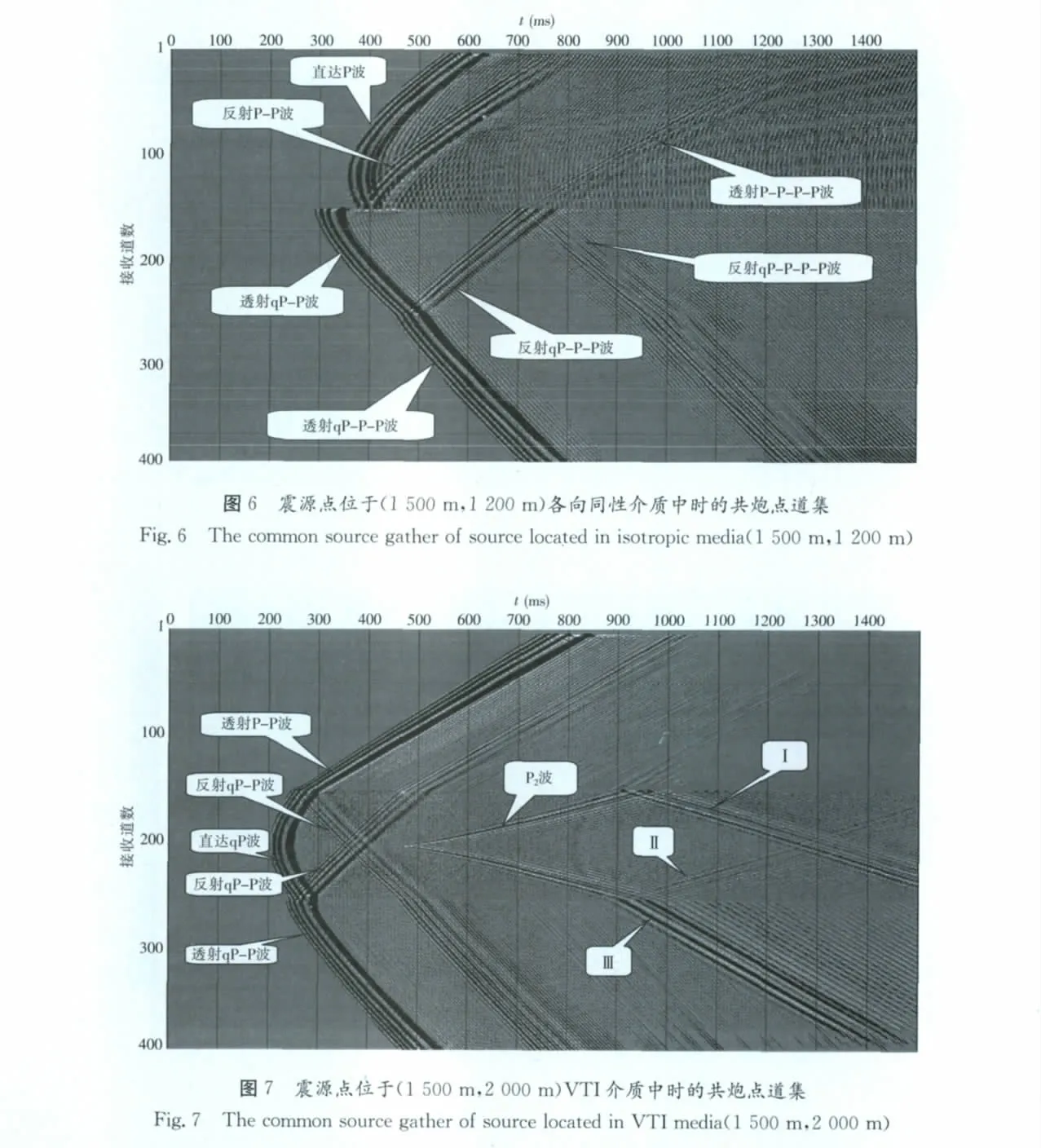
（3）震源位于VTI介質中時，不僅產生縱波還產生實際介質中并不存在的P2波，此波向上傳播到各向同性介質交界面處將產生反射波（見圖7中標注I波）；當向下傳播到VTI介質的交界面處將產生反射波（見圖7中標注II波）和透射波（見圖7中標注III波）。得知P2波只產生于VTI介質中，在各向同性介質中不會產生P2波，因此實際地質條件下，我們只需將震源放在沉積相對比較穩定可以近似認為各向同性的地層中進行激發，就可以有效地消除P2波的影響。

3 結論

應用緊致交錯網格有限差分對井間地質模型進行數值模擬，結果表明：

（1）緊致交錯網格能準確模擬VTI介質中準P波的傳播過程，得到的井間地震波場齊全、清晰。克服了彈性波場正演模擬波場復雜、計算效率低、彈性參數不明確等缺點。

（2）完全匹配層吸收邊界能夠有效解決人工邊界問題，并且和計算區域交界面處產生虛假反射很小，是一種理想的吸收邊界條件。

（3）地震各向異性的研究，使地震學理論向實際地球介質波動理論研究邁出了一大步。隨著對地震精度要求的不斷提高，基于各向異性的處理解釋技術也受到人們越來越多的重視。一階準P波方程能高精度地描述VTI介質中準P波的特征，具有較高的近似精度，在縱波勘探領域有著廣闊的應用前景。

（4）在井間二維VTI介質中準P波的數值模擬方面，將震源置于各向同性介質中激發可以消除計算誤差產生的P2波影響，但是還需進一步研究更好的去除P2波的方法，使震源位于VTI介質時也能去除P2波的影響。

［1］ 周建宇，何惺華，李安夏，等.羅家地區井間地震方法與效果［J］.石油地球物理勘探，2001，36（6）：745.

［2］ 孔慶豐，王延光，左建軍，等.井間地震有限角度疊加方法研究與應用［J］.石油地球物理勘探，2007，42（3）：256.

［3］ 李萬萬，裴正林.井間地震彈性波傳播特征數值模擬［J］.物探與化探，2008，32（2）：207.

［4］ ZHANG J F.VERSCHUUR D J.Elastic wave propagation in heterogeneous anisotropic media using the lumped finite－element method［J］.Geophysics，2002，67（2）：625.

［5］ 祝賀君，張偉，陳曉非.二維各向異性介質中地震波場的高階同位網格有限差分模擬［J］.地球物理學報，2009，52（6）：1536.

［6］ 汪利民，徐義賢，江貴.井中和井間地震波場正演模擬［J］.石油物探，2009，48（2）：146.

［7］ 韓令賀，何兵壽.VTI介質一階準P波方程正演模擬及邊界條件［J］.石油地球物理勘探，2010，45（6）：819.

［8］ ALKHALIFAH T.An acoustic wave equation for anisotropic media［J］.Geophysics，2000，65（4）：1239.

［9］ HESTHOLM S.Acoustic VTI modeling using high－order finite－differences［J］.Geophysics，2009，74（5）：T67.

［10］MADARIAGA R.Dynamics of an expanding circular fault［J］.BSSA，1976，66（3）：639.

［11］LELE S K.Compact finite difference schemes with spectral－like resolution［J］.J.Comput Phys，1992，103（1）：16.

［12］王書強，楊頂輝，楊寬德.彈性波方程的緊致差分方法［J］.清華大學學報：自然科學版，2002，42（8）：1128.

［13］馬廷福，金濤，曹福軍，等.三維雙調和方程的高階緊致差分格式及其多重網格方法［J］.蘭州理工大學學報，2010，36（3）：142.

［14］葛永斌，劉國濤.三維Helmholtz方程的高階隱式緊致差分方法［J］.工程數學學報，2010，27（5）：853.

［15］NAGARAJAN S.LELE S K，FERZIGER J H.A robust high－order compact method for large eddy simulation［J］.Comput.Phys，2003，191（2）：392.

［16］BENDIKS.A staggered compact finite difference formulation for the compressible Navier－Stokes equations［J］.Comput.Phys，2005，208（2）：675.

［17］董良國，馬在田，曹景忠，等.一階彈性波方程交錯網格高階差分解法［J］.地球物理學報，2000，43（3）：411.

［18］DU Q Z，LIN B，HOU B.Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered－grid finite difference scheme［J］.Applied Geophysical，2009，6（1）：42.

［19］COLLINO F，TSOGKA C.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in an isotropic heterogeneous media［J］.Geophysics，2001，66（1）：294.

［20］何兵壽，張會星.VTI介質中準P波方程的數值解法［J］.煤炭學報，2006，31（4）：446.

［21］TARIQ A.An acoustic wave equation for anisotropic media［J］.Geophysics，2000，65（4）：1239.

［22］吳律.層析基礎及其在井間地震中的應用［M］.北京：石油工業出版社，1997.

P 631.4

A

10.3969／j.issn.1001－1749.2012.05.02

1001—1749（2012）05—0510—08

2011－12－06 改回日期：2012－05－17

孟凡順（1960－），男，博士后，教授，主要從事地震波數值模擬與層析成像研究。