用軌跡球實現地物化資料三維立體圖的旋轉
袁小龍,段新力,畢 武,彭仲秋,黃顯義,李永華
(1.新疆地礦局 物化探大隊,新疆 昌吉 830011;2.烏魯木齊金維圖文信息科技有限公司,新疆 烏魯木齊 830091)
用軌跡球實現地物化資料三維立體圖的旋轉
袁小龍1,2,段新力1,2,畢 武1,2,彭仲秋1,2,黃顯義1,2,李永華1,2
(1.新疆地礦局 物化探大隊,新疆 昌吉 830011;2.烏魯木齊金維圖文信息科技有限公司,新疆 烏魯木齊 830091)
為了從各個角度觀察屏幕上的三維場景,可以通過鼠標的拖動來實現。通常的做法是使場景繞X、Y、Z旋轉,但這樣操作不方便,旋轉效果不理想。有一種更好的方法是:為三維場景建立一個外接球,旋轉外接球的同時旋轉了球體內的三維場景,這種技術叫軌跡球技術。這里介紹了軌跡球技術的數學原理、計算方法,并用軌跡球技術在OpenGL環境下實現了地物化資料三維立體圖的旋轉,操作起來方便直觀,人機交互體驗良好。
軌跡球;虛擬球;三維旋轉;四元數
0 前言
隨著計算機硬件、軟件技術水平的發展,地物化數據圖形表現形式越來越豐富。用三維圖形顯示地物化資料數據,形象直觀,易于理解。為了從各個角度觀察場景,可以通過旋轉不同的坐標軸來實現。但旋轉坐標軸操作復雜,不易理解,用戶使用不方便,作者在本文提出了使用軌跡球來解決這個問題。軌跡球技術是由Ken Shoemake提出的,假設場景中所有物體都包含在一個球體中,撥動這個球體,使其繞球心旋轉,這樣球體內的物體跟著旋轉,就可以達到旋轉物體的目的。在計算機操作中,屏幕上創建一個包含所有物體的軌跡球,通過鼠標在二維屏幕上的移動,模擬旋轉球體,可人機交互良好地實現三維場景的旋轉。
1 軌跡球坐標系的建立
(1)屏幕上的設備坐標稱為屏幕坐標,如下頁圖1(a)所示,矩形左上角坐標為(0,0),右下角坐標為 (w,h),w為視圖的寬度,h為視圖的高度,屏幕坐標以像素為單位,X方向朝右為正,Y方向朝下為正。
(2)定義正方形坐標系,如下頁圖1(b)所示,正方形左下角坐標為(-1,-1),右上角坐標為(1,1),中心點坐標為(0,0),X 方向從左向右增大,Y方向從下向上增大。
(3)將屏幕坐標 (screenX,screenY)轉換到正方形坐標(square X,squareY)系內。在X方向,將坐標從范圍(0,width)轉換到(-1,1),坐標變換為線性變換,令
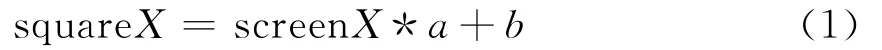
當screenX=0時,square X=-1;當screenX=width時,square X =1。將以上參數代入公式(1),得將a、b值代入公式(1),得到X 方向坐標轉換函數公式(2)。同理,可計算出Y方向坐標轉換函數公式(3)。
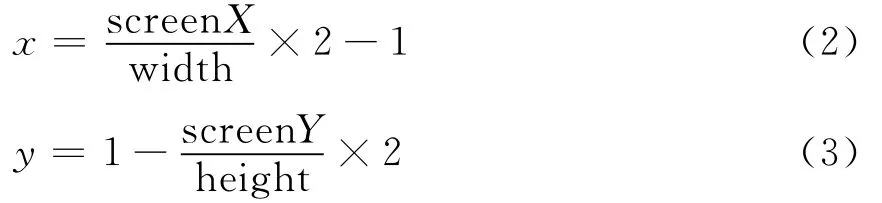
這樣轉換后的坐標X范圍為[-1,1],Y范圍為[-1,1],屏幕中心點坐標為(0,0)。
(4)做正方形的內切圓,如圖1(c)所示。內切圓以它的任意一條直徑為軸,旋轉180°,形成一個球體,如圖1(d)所示。設球體的中心為(0,0,0),半徑為1,我們把這個球體稱為軌跡球,軌跡球上的坐標系稱為軌跡球坐標系。
(5)將正方形坐標 (x,y)轉為軌跡球坐標(u,v,w)。首先,把正方形內的點分成兩部份,一部份在其內切圓內,另一部份在其內切圓之外。鼠標點擊的位置 (x,y)落在內切圓內,即時,以(x,y)為基點,做垂直于屏幕的射線,與軌跡球的外半球(屏幕上能看到的半球)相交于P點,如圖1(e)所示。在拖動鼠標時,相當于以P點為基點拖動球體,鼠標點擊的位置P(x,y)落在內切圓之外,即時,如圖1(f)所示。基點P在軌跡球之外,無法拖動球體,必須重新找一個在軌跡球上的基點,在uov平面內,連接OP,OP交內切圓于P’點,以P’點為基點拽動軌跡球。設θ為OP與OU的夾角,可得:
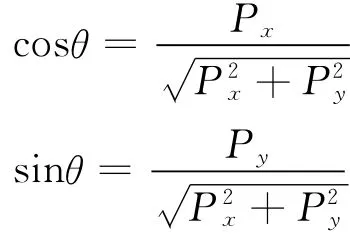
因軌跡球半徑為1,可得:
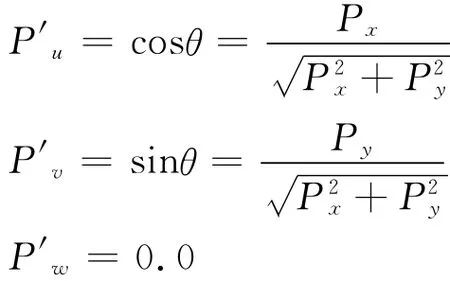
綜合鼠標點擊位置落在內切圓內和內切圓外兩種情況,可得公式(4)。
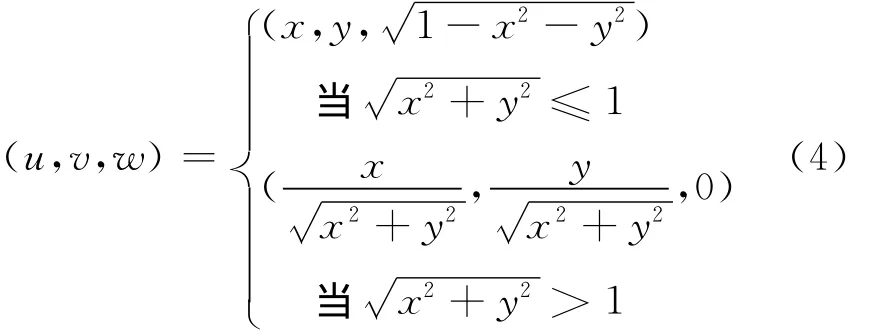
2 旋轉向量的計算
(1)旋轉軸及旋轉角度的確定。如圖2(a)所示,鼠標從P1點移動到P2點,得到兩個矢量,旋轉所張成平面的法向量,通過計算的叉乘,可得到旋轉軸
旋轉角度為OP1與OP2之間的夾角θ,在圖2(a)中,M為正方形左邊的中點,N為正方形右邊的中點,鼠標從M點拖動到N點時,軌跡球繞V軸旋轉了180°,同樣操作,如果要使軌跡球繞V軸旋轉360°,則旋轉角度得取θ的二倍。在實際使用過程中,旋轉角度α取θ的二倍更符合用戶習慣。
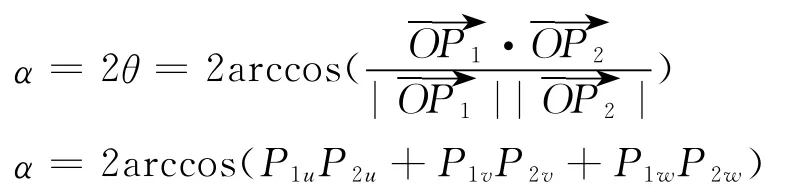
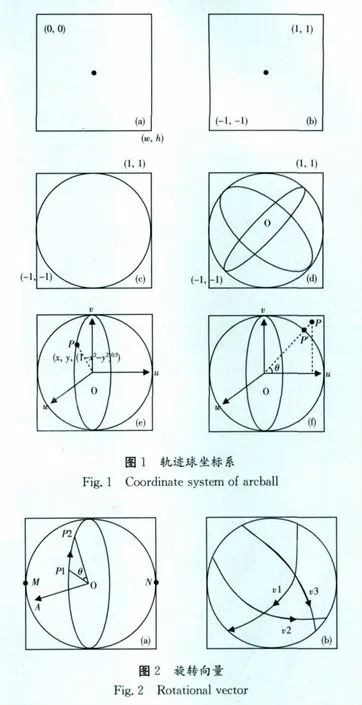
(2)多次旋轉累加。如果鼠標進行了多次拖動,則需要將多次拖動的效果累加起來。如圖2(b)所示,第一次拖動的旋轉量為,第二次拖動的旋轉量為
(3)旋轉矩陣的計算。四元數 Quat4(x,y,z,w)用來存儲旋轉軸和旋轉角度,設 (a,b,c)為旋轉軸向量,θ為旋轉角度,根據四元數旋轉公式:
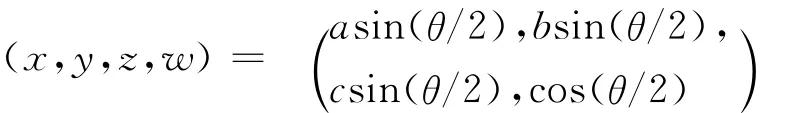
如果鼠標進行了兩次以上的拖動操作,則需將多次旋轉效果進行累加。設Q1(w1,x1,y1,z1),Q2(w2,x2,y2,z2)為兩次旋轉的四元數,將兩次旋轉效果累加按公式(5)計算。
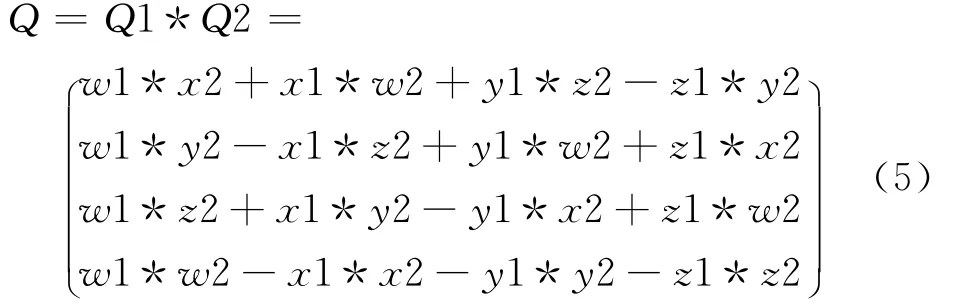
注意:Q=Q1*Q2中,先進行的是右邊項Q2的旋轉,再進行左邊項Q1的旋轉。將最終累加的四元數轉換成旋轉矩陣M[2],在OpenGL中乘以這個旋轉矩陣M,實現軌跡球的旋轉。旋轉矩陣M按公式(6)計算。
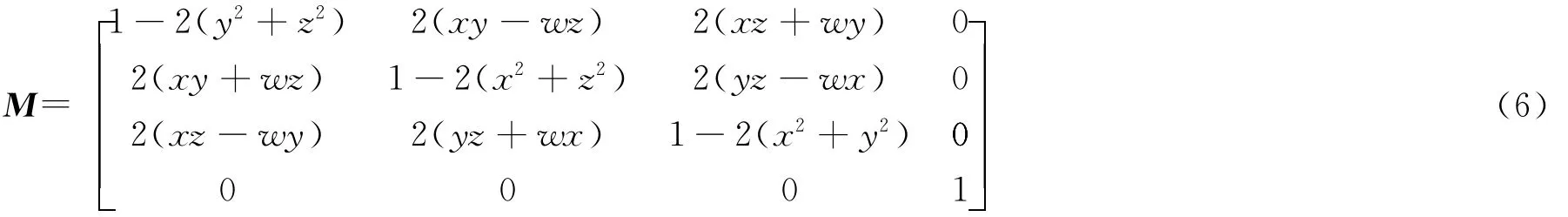
3 軌跡球旋轉地物化三維立體圖實例
用OpenGL函數建立三維地質體模型,在鼠標移動的響應函數中,通過軌跡球計算出旋轉矩陣,當前模型視圖矩陣乘以旋轉矩陣,實現旋轉操作。
(1)實例1:對布格重力網格數據做切割法場分離,切割出五層(一層為一個網格距)的區域場和剩余場,把布格重力和五層剩余異常放在一起顯示,如圖3所示。用軌跡球旋轉操作,可以輕松地旋轉到用戶想要的任意位置。
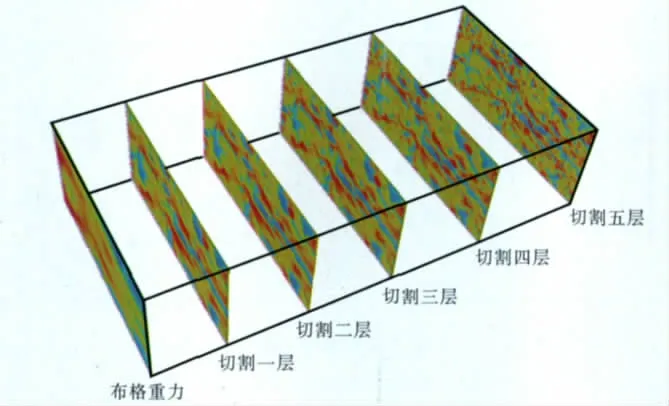
圖3 用軌跡球旋轉重力三維圖Fig.3 Rotating 3Dgraphics of gravity by using arcball
(2)實例2:在鉆孔數據上,通過平行輪廓線截面法創建礦體模型,用軌跡球旋轉操作可以從各個角度觀察礦體及鉆孔。如圖4所示。
4 結束語
作者在本文討論了軌跡球坐標系的建立,旋轉軸及旋轉角度的計算,用四元數表達旋轉向量,多次旋轉效果的累加,以及四元數轉換成旋轉矩陣。在OpenGL環境下編程實現了三維地質模型體繞任意軸旋轉,并給出了兩個實例,用戶可以用二維設備(鼠標)輕松、直觀地旋轉三維場景。

圖4 用軌跡球旋轉礦體及鉆孔Fig.4 Rotating 3Dgraphics of drill hole and ore body by using arcball
[1] MICHAEL CHEN,S.JOY MOUNTFORD.A study in Interactive 3-D Rotation Using 2-D Control Devices[J].Computer Graphics,1988,22(4),121.
[2] SHOEMAKE KEN.Animating Rotation with Quaternion Curves[J].Computer Graphics,1985,19(3):245.
[3] SHOEMAKE K,DUFF T.Matrix animation and polar decomposition[C].In:Procee-dings of Graphics Interface'92,1992.
[4] 馬新武,趙國群,王廣春.用虛擬球實現交互式OpengGL 3D圖形的旋轉[J].計算機應用,2001,21(8):169.
[5] 賴朝輝,劉修國,花衛東,等.三維數據場可視化技術在數字礦山中的應用[J].金屬礦山,2008(12):131.
[6] 李超玲,楊東來,李豐丹,等.中國數字地質調查系統的基本構架及核心技術的實現[J].地質通報,2008,27(7):923.
[7] 黃杏元,馬勁松.地理信息系統概論(第三版)[M].北京:高等教育出版社,2008.
[8] 唐圣潔.三維數據場可視化[M].北京:清華大學出版社,2000.
[9] 屈紅剛,潘懋,王勇,等.基于含拓撲剖面的三維地質建模[J].北京大學學報:自然科學版,2006,42(6):717.
TP 317.4
A
10.3969/j.issn.1001-1749.2012.05.22
1001—1749(2012)05—0622—03
2011-11-24 改回日期:2012-06-16
袁小龍(1982- ),男,本科,主要從事物化探軟件開發、數據處理和資料研究工作。

