中美兩國混凝土規(guī)范配筋計算的差異對比

昝子卉

（廣州地鐵設計研究院，廣東深圳 518000）

中美兩國混凝土規(guī)范配筋計算的差異對比

昝子卉

（廣州地鐵設計研究院，廣東深圳 518000）

以混凝土簡支梁為例，將中美兩國混凝土規(guī)范在受彎配筋和受剪配箍的計算進行對比，并將兩國規(guī)范中構造規(guī)定的最小配筋率、最小配箍率進行對比。通過對比反映出兩國規(guī)范使用的差異，進而使我們對兩國規(guī)范的計算規(guī)則乃至結構安全度方面的差異有進一步的理解。

中國混凝土規(guī)范，美國混凝土規(guī)范，最小配筋率，最小配箍率

隨著國際工程的日益增加，我國工程技術人員越來越多使用到美國規(guī)范。本文提及的美國規(guī)范是指美國混凝土協(xié)會規(guī)定的美國房屋建筑混凝土結構規(guī)范（ACI 318-05）及條文說明（ACI 318R-05）［Building Code Requirements for Structural Concrete（ACI 318-05）and Commentary（ACI318R-05）］。相對于我國工程技術人員普遍熟悉的中國規(guī)范是指現(xiàn)行國標GB 50010-2002混凝土結構設計規(guī)范［code for design of concrete structure］，從整體上說美國混凝土結構設計所用的可靠度表達方式與我國規(guī)范有一定的相似之處，但在設計使用荷載和設計使用材料強度的取值水準上以及構造要求上與我國規(guī)范有著不可忽視的區(qū)別。本文以常用的混凝土簡支梁受彎配筋和受剪配箍計算為例，通過對兩國規(guī)范公式和構造要求的對比，對美國規(guī)范計算規(guī)則進行介紹，并將其與中國規(guī)范進行對比，以期對兩國規(guī)范的計算規(guī)則以及結構安全度有一定的認識。

1 中美混凝土規(guī)范中的設計方法

中國混凝土規(guī)范是基于概率論的承載能力極限狀態(tài)計算法，對荷載和結構承載力乘以相應的分項系數(shù)表達。其表達式為:

其中，γ0為重要性系數(shù);S為荷載效應組合的設計值;R為結構構件承載力的設計值（抗震設計時應除以抗震調(diào)整系數(shù)γRE）。

美國規(guī)范是基于可靠度理論，采用荷載抗力系數(shù)法，其承載力極限狀態(tài)表達式為:

其中，Wn為荷載組合的設計值;Rn為結構構件承載力標準值，由混凝土強度、鋼筋強度、幾何參數(shù)的函數(shù)確定;φ為構件承載力折減系數(shù)，對正截面受彎計算φ=0.9，抗剪計算φ=0.75。

從兩國規(guī)范公式看最主要的區(qū)別在于美國規(guī)范沒有分項系數(shù)，而是采用承載力折減系數(shù)的方法。

2 材料強度轉換

2.1 混凝土強度

中國規(guī)范中，混凝土的強度以立方體抗壓強度標準值劃分為14個等級，常用的有C15，C20，C25，C30，C35，C40等，最高強度等級C80。美國規(guī)范中混凝土采用圓柱體抗壓強度，等級為3000psi （國標C24.5），4000psi（國標C32），5000psi（國標C40），6000psi （國標C49），保證率為91%。表1以中國規(guī)范規(guī)定的混凝土強度為基準，給出兩國規(guī)范對應的混凝土強度指標轉換關系。

表1 兩國規(guī)范對應的混凝土強度指標轉換關系

2.2 鋼筋強度

美國規(guī)范鋼筋屈服強度fy與中國規(guī)范規(guī)定的fyk相同，其使用的鋼筋主要有40級，60級和75級三種，其規(guī)定的屈服強度為280 MPa，420 MPa，520 MPa。與中國規(guī)范不同的是中國規(guī)范采用抗拉強度設計值作為計算依據(jù)，美國規(guī)范以抗拉強度標準值作為計算依據(jù)。

3 正截面受彎配筋計算

3.1 計算假定和公式

美國規(guī)范的基本假定:1）混凝土最外邊緣處受壓纖維的最大應變ε=0.003;2）不考慮混凝土的抗拉強度;3）混凝土應力圖簡化原則（如圖1所示）:混凝土應力0.85ft分布在β1x0的范圍內(nèi)（fc≤28 MPa時β1=0.85，fc＞28 MPa時超過7 MPa，β1減少0.05，且β1≥0.65）。

根據(jù)以上假定，由平衡條件可以得:

其中，Mu為設計彎矩，kN·m;φ為折減系數(shù)，對于正截面抗彎取0.9。

圖1 混凝土應力圖

解上式:

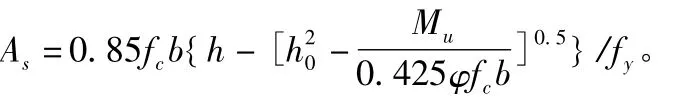
兩國規(guī)范相同的是不考慮混凝土抗拉強度，不同的是在混凝土應力簡化分布中，混凝土應力α2fc分布在β2x0范圍內(nèi)，混凝土強度不超過C50時，β2=0.8，α2=1.0。

對于C50以下等級的混凝土，中美規(guī)范中配筋差異較大。

3.2 正截面構造配筋要求

由以上兩個公式比較可得:美國規(guī)范規(guī)定的正截面最小配筋率大于中國規(guī)范。

4 有腹筋梁受剪承載力計算

4.1 抗剪承載力計算公式

我國混凝土規(guī)范將集中荷載和均布荷載構件受剪承載力計算公式分開。

集中荷載作用下有腹筋梁受剪承載力計算公式為:

均布荷載作用下有腹筋梁受剪承載力計算公式為:

而美國規(guī)范將梁抗剪承載力統(tǒng)一為一個計算公式為:

其中，fyv為箍筋抗拉強度設計值;Asv為箍筋截面面積;ft為混凝土抗拉強度;b為截面寬度;h0為截面有效高度。

從上述公式可以看出，美國規(guī)范對混凝土抗剪強度均考慮了剪跨比的影響，中國規(guī)范對均布荷載在公式中未考慮剪跨比影響，簡單用系數(shù)0.7代替，是不夠合理的。

4.2 抗剪構造配箍要求

美標考慮避免荷載突變斜截面產(chǎn)生太大拉應力導致梁的脆性破壞，規(guī)定構造要求最小配箍率為:

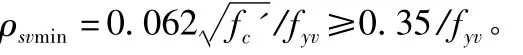
中國規(guī)范為避免梁斜拉破壞，規(guī)定了最小配箍率ρsvmin= 0.062ft/fyv。

以HPB235鋼筋為例，兩國規(guī)范規(guī)定的最小配箍率對比如圖2所示。

圖2 中美兩國規(guī)范最小配箍率對比

5 結語

1）對正截面抗彎配筋計算，C50以下的普通簡支梁相同荷載在忽略試樣尺寸差異情況下，由于計算假定和簡圖的不同導致正截面配筋按美國規(guī)范比中國規(guī)范多20%左右。從構造要求看正截面最小配筋率美國規(guī)范要比中國規(guī)范大，說明其在控制少筋破壞的限制上嚴過中國規(guī)范。2）對斜截面抗剪承載力，剪跨比是影響混凝土抗剪性能發(fā)揮的重要參數(shù)，美國規(guī)范整體考慮了剪跨比對抗剪性能發(fā)揮的影響，而我國規(guī)范僅僅對在集中荷載作用梁的考慮，對分布荷載作用并未考慮剪跨比的影響，不夠合理。3）兩國規(guī)范規(guī)定的最小配箍率都隨著混凝土強度等級增加而增加，反映了混凝土強度等級越高材料脆性越大，發(fā)生脆性破壞可能性提高，因此對應的最小配箍率就大;對比兩國規(guī)范，混凝土強度等級大于C30時，美標中構造要求最小配箍率小于我國規(guī)范的規(guī)定，在對斜拉破壞的限制上中國規(guī)范嚴于美國規(guī)范;對低標號混凝土中國規(guī)范無最小配箍率的下限，但由于實際工程中梁混凝土等級一般都高于或等于C30，并未對實際工程產(chǎn)生影響。

［1］GB 50010-2002，混凝土結構設計規(guī)范［S］.

［2］ACI committee 318.“Building Code Requirements for structural Concrete（ACI318-02）and Commentary（ACI 318R-02）”A-merican Concrete Institute.

［3］尼爾遜AH.混凝土結構設計［M］.過鎮(zhèn)海，方鄂華，譯.北京：中國建筑工業(yè)出版社，2003.

［4］張維秀，王巖.中美規(guī)范鋼筋混凝土梁配筋分析［J］.石油化工設計，2011，28（2）：61-62.

On com parison of differences in reinforcement calculations of concrete regulations in China and America

ZAN Zi-hui

（Guangzhou Metro Design and Research Institute，Shenzhen 518000，China）

Taking the concrete simply supported beams as the example，the study compares the calculations of the flexural reinforcement and the shearing stirrup of concrete regulations in China and America，undertakes the comparison for theminimum reinforcement ratio and theminimum stirrup ratio in the structure regulation of the two countries，and reflects the differences in the application of the regulations of the two countries，so as to have the further understanding of the differences in the calculation rules and the structural safety of the regulation in two countries.

Chinese concrete regulation，America concrete regulation，minimum reinforcement ratio，minimum stirrup ratio

TU375

A

10.13719/j.cnki.cn14-1279/tu.2012.19.140

1009-6825（2012）19-0047-02

2012-03-21

昝子卉（1983-），男，碩士，助理工程師