解排列組合問題的“幾先幾后”
☉山東省日照實驗高級中學 孫先進
解排列組合問題的“幾先幾后”
☉山東省日照實驗高級中學 孫先進
學生在求解排列組合問題時,最常犯的錯誤是分類、分步不清,重復或遺漏計數等,且這些錯誤的發生不易被檢驗出來,造成這種現象的原因是對解決排列組合問題的相關策略沒有理解到位,下面提出幾種策略,供參考.
一、先考慮分類,后考慮分步
對排列組合問題的設置,經常伴有一些約束條件,解決這類問題應先按元素性質進行分類,再按事情發生的連續過程分步處理.
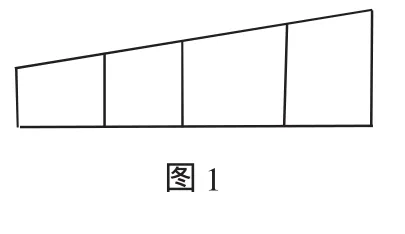
例1 如圖1,用6種不同的顏色給圖中的4個格子涂色,每個格子涂一種顏色,要求最多使用3種顏色且相鄰的兩個格子顏色不同,則不同的涂色方法共有____種.(用數字作答)
解析:由題意可分兩類:

二、先考慮順序后考慮計算
兩個計數原理是解決此部分內容的重要工具,元素是否重復,有無順序,是判斷一個問題的解決是用計數原理還是用排列組合數公式的依據.
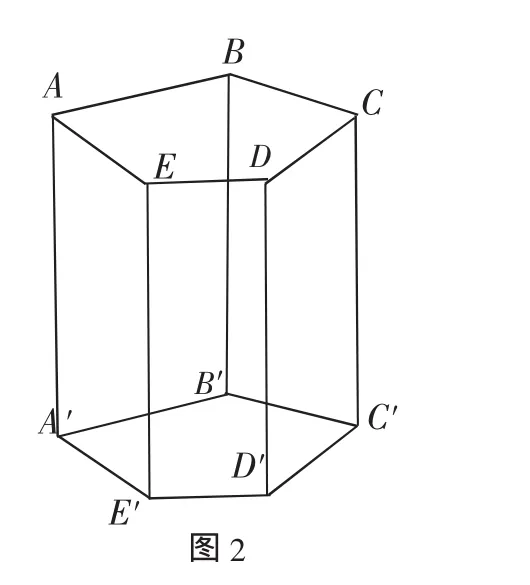
例2 已知正五棱柱ABCDEA′B′C′D′E′(如圖2),現從10個頂點中任意取5個頂點,則可組成多少個不同的四棱錐?
錯解:(1) 第一步,從A、B、C、D、E中任意取4個點組成四棱錐的底面,有5種不同的方法;
(2)第二步,從A′、B′、C′、D′、E′中任意取1個點組成四棱錐的頂點,有5種不同的方法.由分步乘法計數原理,不同的取法共有N=5×5=25(種).
同理,從A′、B′、C′、D′、E′中任意取4個點組成四棱錐的底面,從A、B、C、D、E中任意取1個點組成四棱錐的頂點,也有25個.
所以共有50個不同的四棱錐.
剖析:四棱錐的特點是其中底面四個頂點在同一平面內,另一點不在平面內即可.而錯解中忽略了例如A、B、A′、B′,A、C、C′、A′,A、B、E′、C′等也在同一平面內的情況.
正解:在錯解的基礎上,另外還有以ABA′B′為底面,從C、D、E、C′、D′、E′中任取一點為頂點,有6個四棱錐.同理,以BCB′C′、CDC′D′、DED′E′、AEA′E′為底面分別有6個四棱錐,則共有30個四棱錐;以ACC′A′為底面,從B、E、D、B′、E′、D′中任取一點為頂點,有6個四棱錐,同理,以BDD′B′、CEE′C′、DAA′D′、EBB′E′為底面分別有6個四棱錐,則共有30個四棱錐;以ABE′C′為底面,從C、D、E、A′、B′、D′中任取一點為頂點,有6個四棱錐.同理,以BCD′A′、CDE′B′、DEA′C′、EAB′D′、A′B′EC、B′C′DA、C′D′EB、D′E′AC、E′A′BD為底面分別有6個四棱錐,則共有60個四棱錐.所以共有N=25+25+30+30+60=170(個).
共有170個不同的四棱錐.
三、先考慮定性,后考慮定量
當題目的條件比較籠統、不明確時,一般應先分好明確的類別或者步驟,再用相應的原理解決.
例3 從5名男生和4名女生中任選3人,要求至少有男生和女生各一人的選法有( )種.
A.70 B.140 C.84 D.35

剖析:事實上,不妨設5名男生分別為甲、乙、丙、丁、戊,4名女生分別為A、B、C、D.當先分別選1名男生和1名女生時,選到了男甲女A,再在剩下的7人中任選1人時,選到了男乙,從而選到三人的一種方式為男甲女A男乙.當先分別選1名男生和1名女生時,若選到了男乙女A,再在剩下的7人中任選1人時,選到了男甲,這時選到三人的一種方式為男甲女A男乙.這兩種方式是同一種選法,因此,上述解法中有重復現象,從而是錯誤的.要想正確解答該題,關鍵在于應對題設條件“至少有男生和女生各一人”給出具體的分類,明確到底有幾名男生,幾名女生.
正解:完成事件分為兩類:選1名男生、2名女生和選2名男生、1名女生.

四、先考慮特殊,后考慮一般
某些排列組合問題中帶有特殊元素或特殊位置的排列組合題,對此類問題的處理一般應先考慮特殊情況,本著特殊者優先的原則處理.
例4 用0到9這10個數字,可以組成沒有重復數字的三位偶數的個數為( ).
A.324 B.328 C.360 D.648
解析:因為“0”是特殊元素,它不能排在最前面,所以分兩種情況考慮.
因此由分類計數原理,符合題意的偶數共有72+256=328(個).故選擇B.
對于受限制的特殊元素(或位置)的排列組合問題,要先安排“特殊”元素(或位置),再安排其他沒有限制的元素或位置.因此特殊元素(位置)用優先法.
例5 某地奧運火炬接力傳遞路線共分6段,傳遞活動分別由6名火炬手完成.如果第一棒火炬手只能從甲、乙、丙三人中產生,最后一棒火炬手只能從甲、乙兩人中產生,則不同的傳遞方案共有________種.

五、先考慮組合,后考慮排列
對于排列組合的混合問題,一般采取先選出元素即分組,再進行排列的原則解決問題.
例6 將4個不同的小球放入編號為1、2、3、4的四個盒子中,則恰有一個空盒的方法有_______種.
解析:這是一個排列組合的混合問題.因恰有一個空盒,所以必有一個盒子要放2個球.故可分兩步進行.第一步,先分組.從4個球中任選2個球,有種選法,從4個盒子中選出3個,有種選法.
第二步,進行排列.把選出的2個球視為一個元素,與其余的2個球共3個元素對選出的3個盒子作全排列,有種排法.

六、先考慮總體,后考慮個體
例7 在某種信息傳輸過程中,用4個數字的一個排列(數字允許重復)表示一個信息,不同排列表示不同信息,若所用數字只有0和1,則與信息0110至多有兩個對應位置上的數字相同的信息個數為( ).
A.10 B.11 C.12 D.15
解析:此題用直接法進行分類求解較為復雜,故想到排除法,先求出與0110有三個位置或四個位置上的數字相同的排法,再用允許數字重復的總排列數相減即可.用0和1進行排列,允許數字重復共有16種排法,因為與0110有三個位置上的數字相同的排法有四種:1110、0010、0100、0111,與0110有四個位置上的數字相同的只有一種排法,所以與信息0110至多有兩個對應位置上的數字相同的信息個數有16-4-1=11(種).故選擇B.
有些問題從正面直接考慮比較復雜,而從它的反面往往比較容易思考時,可以先求出它的反面,再從整體中排除.因此至少或至多問題應采用排除法.

