凹版印刷機干燥箱流體動態分析及參數優化

武吉梅，徐宗磊，陳允春，薛志成，劉琳琳

(1.西安理工大學 印刷包裝工程學院，西安 710048;2.陜西北人印刷機械有限責任公司，陜西 渭南 710000;3.山推工程機械股份有限公司，山東 濟寧 272073)

凹版印刷機上，干燥系統是凹印技術的核心技術之一。干燥箱內熱風對印刷品干燥效果直接影響印刷質量。因此，對凹版印刷機干燥箱熱風的動力學特性進行研究，進一步優化干燥箱結構參數，以實現熱風條件的精確控制十分必要。目前已有許多專家學者對熱風干燥參數及流體特性進行了研究。Collet［1］把傳熱物質看做包含很多獨立自由運動的無限介質，并在此基礎上通過利用熵變理論得到熱擴散的數學模型;Cao［2］對干燥管道結果的研究，建立干燥風管內部空氣流動的熱力學模型。黃清明［3］對凹版印刷機干燥箱溫度優化控制系統進行了研究與設計。牛永生［4］研究了利用熱相似理論建立準數學模型換熱的運算式，求出對流換熱系數。本文采用計算流體力學方法(簡稱CFD)建立干燥箱熱風流動模型并進行數值分析，得到熱風在干燥箱中溫度分布并根據結果對其進行優化改進。

1 凹版印刷機干燥方式

目前在凹版印刷機上應用最多的干燥方式為熱風對流干燥［5］。

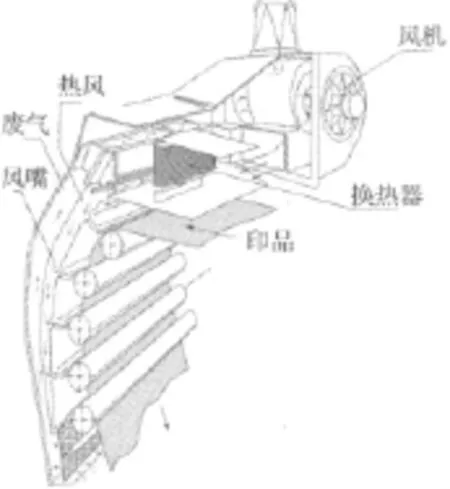
圖1 熱風對流干燥系統圖Fig.1 Drying system of hot-air convection

圖1為熱風對流干燥系統圖。空氣由風機進風口進入風機，獲得一定速度，然后經過換熱器，通過熱量交換，得到印品干燥所需溫度，通過風道進入干燥箱，具有一定溫度、速度的熱風由干燥箱風嘴吹到印品表面，完成印品干燥過程。干燥后廢氣通過排風管道，排入大氣或對其進行二次利用。

為了保證印品干燥的均勻性，除了要準確控制影響干燥的熱風條件之外，還要保證在印品表面熱風的均勻性。本文主要以熱風條件之一——熱風溫度為目標函數分析在干燥箱工作過程中箱內熱風溫度場分布。

2 凹版印刷機干燥系統熱風分析方法

CFD數值計算方法:在熱風控制方程基礎上，添加熱風流動模型和邊界條件，對其進行求解，來描述熱風在干燥箱中熱風溫度場［6］。

2.1 熱風控制方程

2.1.1 連續性方程

控制面質量變化等于微元體內部質量變化［7］，如圖2所示:

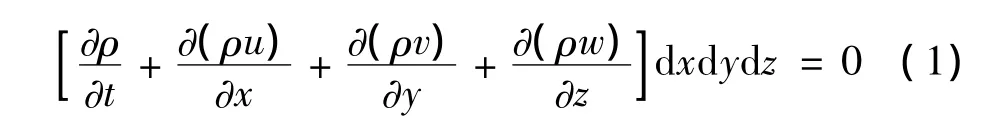
式中:ρ為流體密度;u、v、w為流體在x、y、z方向上的速度。

2.1.2 運動方程

動量的時間變化率等于作用于其上的外力總和。

圖2 微元控制體Fig.2 Infinitesimal control body

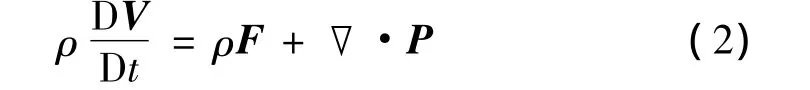
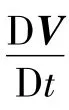
2.1.3 能量方程

能量變化率等于單位時間內外力對它所做的功和傳給它的熱量之和［8］:

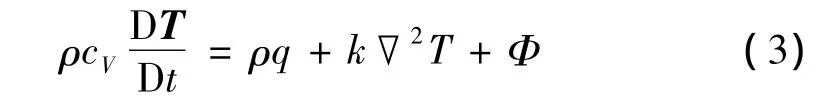
其中:ρ為密度;k為導熱系數;q為熱源項;cV為定容熱容;Φ為耗散函數;DT/Dt為溫度隨體導數。

3 能量損失計算

3.1 兩種管道形狀變化能量損失

式中:hf1為突擴管局部能量損失;hf2為漸擴管局部能量損失，v1為進口速度;A1、A2為進出口截面積;κ為與擴散角有關的系數。經過分析，漸擴管能量損失為突擴管的1/10～3/5。

3.2 圓形導流管能量損失

沿程能量損失hl:

式中:λ為阻力系數;d=A/X為特征長度，A為流體截面積，X為濕周;U為速度;l為管道長度。

4 流體動態數值計算

4.1 實驗驗證

4.1.1 實驗測試

風機:風壓:1 020 Pa;轉速:850 m3/h，實驗如圖3所示:

圖3 實驗測試圖Fig.3 Experimental test

圖4 三維模型Fig.4 3D model

通過實驗測得出口處的風速平均值為27.1 m/s。

4.1.2 CFD 數值分析

(1)建立模型如圖4所示。

(2)數值分析結果，出風口速度分布圖，如圖5所示:

圖5 出口速度分布圖Fig.5 Velocity distribution of export

計算得出口平均速度:24.003 4 m/s。

由結果可知，數值分析與實驗之間存在一定誤差，誤差為10.3%，屬允許誤差范圍。因此，本研究采用CFD分析方法是可行的。

4.2 傳統干燥箱數值分析

4.2.1 傳統干燥箱模型

傳統干燥箱模型如圖6(a)所示。

圖6 傳統干燥箱模型及流體域Fig.6 The model and fluid domain of traditional drying-oven

4.2.2 模型簡化及網格化

進行數值分析計算時，建立連接風機與干燥箱之間的風道及干燥箱內流體域模型如圖6(b)所示。

4.2.3 流體數值計算

本文采用有限體積法及二階迎風格式對控制方程進行離散，添加κ-ε模型為湍流模型，采用SIMPLE算法對控制方程求解［9-10］。

邊界條件如下:① 入口邊界:溫度為360 K，壓力為3 929 Pa，空氣密度為1.228(kg/m3)，粘性系數為1.789e-5(Pa·s)，比熱 1 006.43 J(kg·K)。② 出口邊界:外界大氣壓。

4.2.4 結果分析

干燥箱溫度分布云圖，如圖7所示。

圖7 傳統干燥箱溫度分布圖Fig.7 Temperature distribution of traditional drying-oven

溫度在干燥箱出口處分布均勻性較差，干燥箱中溫度最大值為360 K，最小值為299.99 K。(風嘴由上到下分別為風嘴1～5)。

以風嘴2溫度分布為例，橫坐標代表風嘴長度，縱坐標代表溫度大小，如圖8所示。

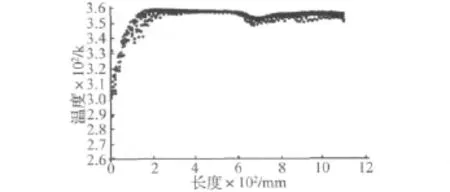
圖8 風嘴2溫度分布圖Fig.8 Temperature distribution of wind-mouth-two

風嘴2溫度分布不均勻，變化范圍比較大，并得到風嘴2平均溫度為351.642 04 K。

采用相同的方法得到其余風嘴的平均溫度。

風嘴 1:357.066 28 K;風嘴 3:337.454 22 K;

風嘴 4:354.889 48 K;風嘴 5:354.489 73 K;

出口平均溫度:351.574 72 K。

根據不同輸入溫度及輸出溫度得出二者之間的關系［11］，以風嘴2溫度為例，如圖9所示:

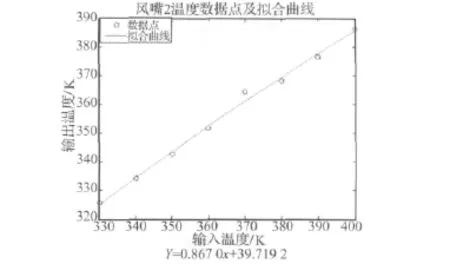
圖9 輸出溫度與輸入溫度關系Fig.9 The relations of output temperature and input temperature

4.3 可視化界面

采用VB語言將輸出溫度與輸入溫度的關系轉化為可視化界面如圖10所示。

圖10 計算界面Fig.10 Calculation interface

根據計算流體力學可知傳統干燥箱溫度均勻性比較差，同時由熱風輸入參數與輸出參數關系可以更加準確控制影響印品干燥的干燥參數。

5 干燥箱改進

熱風溫度在傳統干燥箱中較小并且均勻性較差，主要原因是干燥箱內部存在渦流及風嘴出口面積較大，因此，需要在其內部加入導流管道，同時要加大入風口，由式(4)計算，選用漸擴管。

5.1 風嘴改進

根據式(5)對不同截面積管道計算，得到圓形導流管能量損失較小，所以改進后干燥箱如圖12(a)，流體域如圖12(b)所示，結構參數對照表如表1所示。

圖11 風嘴Fig.11 The wind mouth

圖12 改進后干燥箱及流體域Fig.12 The model and fluid domain of modified drying-oven

表1 干燥箱結構參數對照表Tab.1 The cross-references of drying oven structure parameters

5.2 改進干燥箱分析計算

5.2.1 結果分析

干燥箱溫度分布如圖13所示。

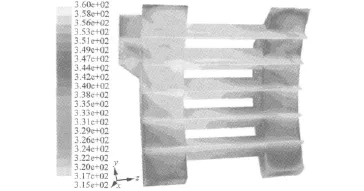
圖13 改進干燥箱溫度分布圖Fig.13 The temperature distribution of modified drying-oven

從圖中得出，溫度在干燥箱出口處分布均勻性相比傳統干燥箱得到了改善。干燥箱中溫度最大值為360 K，最小值為313.183 K。

風嘴2溫度分布，如圖14所示。

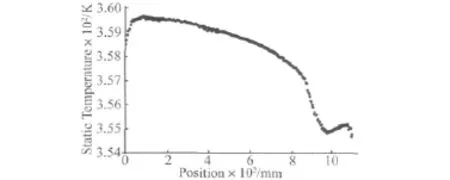
圖14 風嘴2溫度分布Fig.14 The temperature distribution of wind mouth two

由圖得出，溫度均勻性比較好，溫度變化范圍在354～360 K之內。風嘴2溫度平均值為:358.470 21 K。

采用相同方法得出其余風嘴溫度平均值:

風嘴 1:358.863 05 K;風嘴 3:358.934 04 K;

風嘴 4:358.637 38 K;風嘴 5:355.877 98 K;

出口平均溫度:358.558 53 K。

由數值分析結果可以看出干燥箱進行改進后，熱風溫度的大小、分布的均勻性得到了改善，并且溫度損失相比傳統的干燥箱要小的多。

6 對改進后干燥箱進行再次優化設計

改進后干燥箱溫度大小及均勻性得到一定改善，但是在干燥箱右側以及下方，溫度相對較小。

6.1 優化設計干燥箱熱風流動模型

繼續對干燥箱進行優化設計，方法是對右側內腔單獨增加進風管道，并減小內腔下方空間體積。優化設計后干燥箱熱風流動模型如圖15所示。

圖15 優化設計后的模型Fig.15 The model of optimal design

6.2 結果分析

干燥箱溫度分布云圖，如圖16所示。

圖16 優化設計后溫度分布圖Fig.16 The temperature distribution of optimal design

風嘴2溫度分布，如圖17所示。

圖17 風嘴2溫度分布Fig.17 The temperature distribution of wind mouth two

由圖得出，最終優化設計后干燥箱溫度分布均勻性得到改善，并且溫度變化范圍在358～360 K之間，易于對其進行準確控制。

7 結論

本文采用計算流體力學(CFD)方法對傳統干燥箱進行建模分析，并根據分析結果對其進行改進和優化設計，得出以下結論:

(1)傳統干燥箱中熱風溫度分布均勻性較差，溫度變化范圍較大，并且存在渦流現象。

(2)在傳統干燥箱中加入導流管，消除了渦流現象，并且溫度大小及均勻性有所提高。

(3)對改進后干燥箱進行了優化設計，得到熱風溫度均勻性明顯提高，溫度變化在1～2 K，適用于精細印刷，提高印刷速度，同時可以提高對干燥條件控制的準確度。

［1］Collet P，Eckmann J P.A model of conduction［J］.Communication in Mathematical Physics，2009，287(2):1015-1038.

［2］Cao X W，Wang L Y，Lin Z H.Air-drying models for newbuilt offshore gas pipelines［J］.Petroleum Science，2005，29(4):46-51.

［3］黃清明.凹版印刷機干燥箱溫度優化控制系統研究與設計［J］.機械工程師，2008(11):72-74.

［4］牛永生，張長松，路有昌，等.運用熱相似理論確定對流換熱系數［J］.安陽師范學院學報，2000，11(2):30-32.

［5］卑江艷.凹版印刷［M］.北京:化學工業出版社，2002.

［6］王福軍.計算流體動力學分析［M］.北京:清華大學出版社，2004:26-86.

［7］王 軍.流體動力學分析［M］.北京:清華大學出版社，2004.

［8］林建忠.流體力學［M］.北京:清華大學出版社，2005.

［9］王瑞金，張 凱，王 剛.Fluent技術基礎與應用實例［M］.北京:清華大學出版社，2007.

［10］韓占忠，王 敬，蘭小平.FLUENT流體工程仿真計算實例與應用［M］.北京:北京理工大學出版社，2004.

［11］林雪松.MATLAB7.0應用集錦［M］.北京:機械工業出版社，2005.