一類準周期參激非線性扭振系統的周期簇發

時培明，李紀召，劉 彬，韓東穎

(1.燕山大學 電氣工程學院，秦皇島 066004;2.燕山大學 測試計量技術及儀器河北省重點實驗室，秦皇島 066004;3.燕山大學 車輛與能源學院，秦皇島 066004)

旋轉機械是工業部門中應用最為廣泛的一類機械設備，在電力、能源、交通、冶金以及國防等領域發揮著無可替代的作用。而傳動系統作為旋轉機械的核心部分，其運行狀態影響整個生產過程。隨著生產速度和生產規模的逐步提高，傳動系統中的扭振問題也日益突出。傳動系統中存在復雜的非線性因素［1］，諸如間隙、非線性阻尼、非線性剛度等［2-4］，導致系統發生非線性扭振，影響其正常工作甚至導致設備損壞，造成重大的經濟損失。文獻［5］建立含非線性阻尼的非線性轉動系統動力學方程，分析其在強迫激勵下的近似解。文獻［6］對旋轉機械傳動系統的扭振進行了動力學建模與仿真。

簇發現象在神經元模型中已被廣泛地認識［7］。Rinzel［8］首次對神經元的簇放電模式作出了系統的分析，認識到慢變參數對快變量的調節作用引起快變動力學的靜息態和激發態的相互轉遷。Izhikevich［9］對神經應激性、激發、簇發進行了分析。快慢系統中連接快慢兩過程的行為通常稱為簇發。Lakrad等［10］研究了自激準周期Mathieu振子的準周期解和簇發現象。Han等［11］對三環面、準周期簇發，對稱亞臨界hopf/倍周期簇發，亞臨界hopf/倍周期簇發，及它們之間的聯系進行了分析。季穎、畢勤勝［12］研究了非光滑電路簇發行為的分岔機制及多種簇發現象。

在實際旋轉機械的傳動系統中，由于間隙、傾角、裂紋等非線性剛度因素的存在，往往以不同頻率的周期參數激勵的形式同時作用于扭振系統，表現為準周期特性。如裂紋的存在會使轉軸剛度發生周期性的變化，從而使轉子系統產生含有高頻和低頻成份的振動，出現復雜的動力學行為［13］。本文考慮準周期參數激勵，建立一類含有準周期參激剛度和非線性阻尼的扭振系統的動力學方程。研究了當兩種周期激勵的頻率差距較大時系統的周期簇發現象，給出了周期簇發的參數區域，分析了簇發產生的機制，并對改變快變參激和慢變參激的幅值時所引起的快慢系統的靜息態與激發態的變化進行了仿真分析。

1 準周期參激非線性扭振系統動力學方程

旋轉機械是工程中廣泛存在的動力傳動系統，圖1為旋轉機械中傳動系統的兩質量扭振系統動力學模型。設J1、J2為扭振系統集中質量的轉動慣量，θi(i=1，2)分別為兩個集中質量的轉角，F1、F2分別是兩個集中質量的外加力矩。

圖1 二質量扭振系統動力學模型Fig.1 Dynamic model of torsional vibration system with 2-DOF

K為系統的扭轉剛度，θ·i(i=1，2)分別為兩個集中質量的轉速，扭振系統的動能為:

阻尼力表示為:

考慮準周期參激剛度，即:

其中，v為與扭振系統固有頻率相關的共振頻率，Ω為遠小于固有頻率的慢變頻率，ρ'、h'為剛度的變動幅值，K0為等效剛度。扭振系統的勢能U為:

把式(2)和式(3)代入動力學普遍方程

廣義力(廣義力矩)為:

其中，qr(r=1，2)為廣義坐標，n為自由度數目。將式(2)和式(3)代入式(7)后得到系統的廣義力(廣義力矩)為:

將式(1)、式(2)、式(3)、式(5)、式(8)和式(9)代入如下Lagrange動力學方程:

可得:

其中，

其中，ω表示系統的固有頻率。式(14)就是一類含準周期參激剛度和非線性摩阻的非線性扭振系統的動力學方程。

2 準周期參激扭振系統的分岔響應方程

引入參數ε，對準周期參激扭振系統進行攝動分析。將方程(14)中的參數改寫為。則方程(14)可以表示為:

采用多尺度法［14-15］，設方程(15)的攝動解形式為:

將式(16)代入式(15)，可得到各階近似的線性偏微分方程組:

其中，A(T1，τ)和(T1，τ)為共軛函數且均為關于T1的函數。將式(19)代入式(18)中可以得到:

其中，式(20)中cc項表示等式右端各項的共軛復數部分。消除久期項，令:

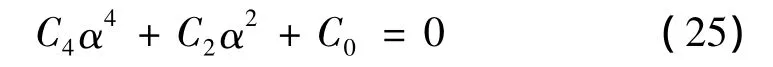
其中，

3 準周期參激扭振系統的周期簇發現象

具有快慢效應的非線性動力系統會產生各種復雜的簇發現象。在靜息態和激發態之間的簇發現象會呈現出復雜的動力學特性。當準周期參數激勵中其中一個參數激勵的頻率遠小于另一個參數激勵的頻率時。會發生簇發現象［16］。本文中Ω?v，系統參數取值為ω=1、α=0.2、β=0.1、σ=-0.2、Ω=0.01。

3.1 快變參激對簇發現象的影響

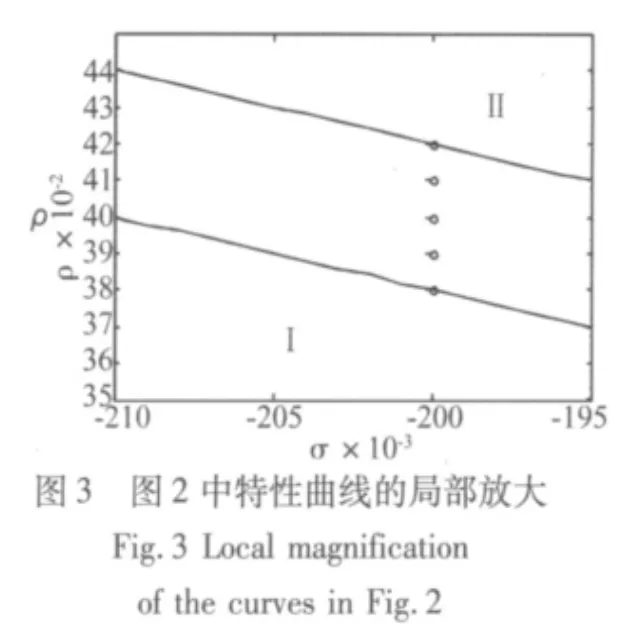
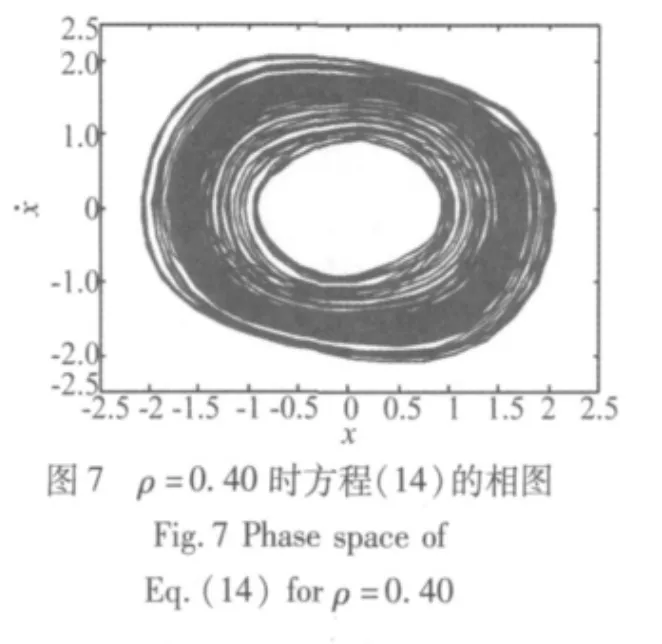
取慢變參激的幅值h=0.02，由于慢變參激項的作用，在分岔響應方程的特性曲線如圖2中的區域Ⅰ和區域Ⅱ之間產生了一個區域。在這個區域內取值時，就會發生靜息態與激發態的相互轉遷，即發生周期簇發現象。將圖2中的部分區域進行局部放大如圖3所示，當快變參數激勵的幅值ρ=0.42時，得到系統的周期簇發解如圖4，圖中靜息態區域較寬，激發態區域較窄并出現一個激發態;減小快變參數激勵幅值到ρ=0.4時，系統的周期簇發解如圖6，靜息態區域變窄，激發態區域增大并出現三個激發態;當快變參數激勵的幅值進一步減小到ρ=0.38時，周期簇發解如圖8，可以看出，靜息態區域繼續減小，激發態增加到五個激發態。圖5、圖7、圖9分別為前面的周期簇發解所對應的相空間，從相圖中可以明顯的看出，靜息態位于相圖的中間的密集部分，靜息態的內側和外側為激發態，隨著快變參數激勵的幅值ρ的減小，靜息態的寬度逐漸變窄，激發態開始活躍。

3.2 慢變參激對簇發現象的影響

取快變參激的幅值ρ=0.5，當h=2時，準周期參激系統的周期簇發解如圖10所示，此時準周期參激系統的動力學特性表現為由相對的大幅值和微小幅值兩種振蕩的組合，大幅值振蕩和小幅值振蕩分別看做準周期參激系統的激發態和靜息態［17-18］。圖11為圖10周期簇發解的局部放大，圖中，隨著時間的推移，會產生雙側不對稱的大幅值振蕩與小幅值振蕩的相互交替現象。周期簇發解所對應的相圖如圖12，圖中系統的運行軌跡為L6→L1→L2→L3→L4→L5→L6，其中的L1→L2及L4→L5段的詳細運行規律如圖13，圖中系統的軌跡為從L1的大幅值振蕩開始，跳變進入中心區域的極限環域變為小幅值振蕩，然后沿著軌跡L2重新躍變為大幅值振蕩。L4→L5段的運行規律與L1→L2段的運行規律類似。

增大慢變參數激勵的幅值，當h=3時，準周期參激系統的周期簇發解如圖14所示。圖15為圖14中周期簇發解的局部放大。時序圖中，隨著時間的推移，會產生單側不對稱的大幅值振蕩與小幅值振蕩的相互交替現象。周期簇發解所對應的相圖如圖16，圖中系統的運行軌跡為L9→L7→L8→L9，其中的L7→L8段的詳細運行規律如圖17，圖中系統的軌跡為從L7的大幅值振蕩開始，跳變進入中心區域的極限環域變為小幅值振蕩，然后沿著軌跡L8從極限環中躍變出來重新變為大幅值振蕩。

圖14 周期簇發解h=3Fig.14 Periodic bursting solution for h=3

圖15 圖14簇發解的局部放大Fig.15 Local magnification of periodic bursting solution in Fig.14

圖16 h=3時方程(14)的相圖Fig.16 Phase space of Eq.(14)for h=3

圖17 圖16相圖的局部放大Fig.17 Local magnification of phase space in Fig.16

4 結論

考慮了旋轉機械傳動系統中兩種不同周期參數激勵共存的情形，建立了一類含準周期參激剛度、非線性摩擦阻尼的非線性扭振系統動力學方程。求解了系統在1/2亞諧波主參數共振下的分岔響應方程，研究了當兩種周期參激的頻率相差較大時非線性扭振系統的周期簇發現象，并給出了產生周期簇發的參數取值區域，在區域改變參數取值，就會發生靜息態與激發態的相互轉遷及周期的改變。當減小快變參數激勵的幅值時，靜息態的時間減少，激發態區域擴大，簇發所占用的時間延長。當改變慢變參數激勵的幅值時，系統的簇發模式及運動軌跡都會發生改變。研究結果為揭示該類旋轉機械傳動系統中的周期簇發動力行為提供參考。

［1］Christof S.A novel torsional exciter for model vibration testing of large rotating machinery［J］.Mechanical Systems and Signal Processing，2006，20(7):1725-1740.

［2］文 明，王新芳，張維奇，等.阻尼及三次非線性因素對具有調諧質量阻尼器的干摩擦隔振系統性能影響的研究［J］.振動與沖擊，2006，25(2):152-158.

［3］李 沈，趙樹森.分支軸系扭振的子結構分析方法研究［J］.振動與沖擊，2007，26(10):148-151.

［4］史文庫，龍 巖，盧玉東.多級非線性雙質量飛輪參數設計和優化［J］.振動與沖擊，2009，28(5):92-96.

［5］時培明，劉 彬.相對轉動非線性動力系統的穩定性與強迫激勵下的近似解［J］.物理學報，2007，56(7):3678-3682.

［6］侯東曉，劉 彬，時培明.旋轉機械傳動系統連續扭振動力學建模與仿真［J］.中國機械工程，2010，21(1):30-34.

［7］Coombes S，Bressloff P C.Bursting:the genesis of rhythm in the nervous system［M］.World ScientificPress，2005.

［8 ］ Rinzel J.Ordinary and partial differential equations［J］.Lecture notes in mathematics，1985，1151:304 316.

［9］ Izhikevich E M.Neural excitability，spiking，and bursting［J］.International Journal of Bifurcation and Chaos，2000，10:1171-1266.

［10］ Lakrad F，Azouani A，Abouhazim N，et al.Bursters and quasi-periodic solutions ofa self-excited quasi-periodic mathieu oscillator［J］.Chaos，Solitons and Fractals，2005，24:813-824.

［11］ Han X J，Jiang B，Bi Q S.3-torus，quasi-periodic bursting，symmetric subHopf/fold-cycle bursting，subHopf/fold-cycle bursting and their relation［J］.Nonlinear Dynamics，2010，61:667-676.

［12］ Ji Y，Bi Q S.Bursting behavior in a non-smooth electric circuit［J］.Physics Letters A，2010，374:1434-1439.

［13］聞邦椿.故障旋轉機械非線性動力學近期研究綜述［J］.振動工程學報，2004，17(1):1-5.

［14］Shi P M，Liu B，Hou D X.Global dynamic characteristic of nonlinear torsional vibration system under harmonically［J］.Chinese Journal of Mechanical Engineering，2009，22(1):132-139.

［15］劉浩然，張業寬，李曉梅，等.軋機非線性傳動系統沖擊扭振的研究與抑制［J］.振動與沖擊，2010，29(7):179-183.

［16］張曉芳，陳章耀，畢勤勝.周期激勵Chen系統的簇發現象分析［J］.物理學報，2010，59(6):3802-3808.

［17］陳章耀，張曉芳，畢勤勝.廣義Chua電路簇發現象及其分岔機理［J］.物理學報，2009，59(4):2326-2333.

［18］陳章耀，張曉芳，畢勤勝.周期激勵下Hartley模型的簇發及分岔機制［J］.力學學報，2010，42(4):765-773.