某螺旋槳長航時無人機氣動力改進設計與分析

劉城斌，李杰，李鑫，周麗瓊

(西北工業大學航空學院，陜西西安 710072)

引言

螺旋槳無人機由于具有推重比大、油耗低、噪聲小和穩定性好等突出優點而被廣泛用于執行中高空情報偵察和長時間的監視任務，如美國的捕食者無人機和以色列的蒼鷺-B無人機等［1］。這類無人機為了長時間巡航需要保持較低的燃料消耗率，因此巡航設計點的速度一般較低，雷諾數基本處于百萬數量級。由于巡航時飛行速度低、空氣密度小，使其對機翼的氣動性能有較高要求。在低雷諾數條件下實現高升力、高續航因子的機翼氣動力設計是螺旋槳長航時無人機開發研制的關鍵技術。

本文針對螺旋槳長航時無人機的設計使用要求，進行了機翼氣動力改進設計和研究。

1 無人機兩段機翼設計思想

1.1 續航性能評價準則

螺旋槳無人機的續航時間可以用布雷蓋公式(Breguet Equation)［2］來計算:

式中，T為續航時間;η為螺旋槳效率;c為單位耗油率;σ為巡航高度大氣密度和海平面大氣密度之比;S為機翼面積;Wi和Wf分別為待機巡邏開始和結束時的飛機重量。該式假定 η，c，CL，CD，σ 和 S為常數，可以看出，螺旋槳無人機的待機續航時間與續航因子/CD相關，而不是升阻比CL/CD。螺旋槳無人機若在最大續航因子(/CD)max所對應的速度和升力系數下飛行，將能達到最大續航時間［3］。

為了增大螺旋槳無人機在待機狀態的最大續航時間和有效載荷，在對無人機機翼進行氣動力改進設計時，主要目標便是有效提高無人機巡航升力系數和續航因子。

1.2 兩段機翼設計原理

提高機翼的氣動性能需要從二維翼型著手進行改進。現役長航時無人機大多使用的是單段翼型，升力和升阻比的可提升空間很小，限制了其氣動性能的進一步提高。相比單段翼型，兩段翼型固有的高升力特性以及翼型上所能夠保持的較長層流區，使其在高升力時可以維持較小的阻力，升阻比要明顯高于相同設計狀態下的單段翼型。當兩段翼型配置到三維機翼上，會出現誘導阻力和較為明顯的寄生阻力，升力和阻力的同時增加使升阻比相比于單段機翼無人機無明顯提高，但由于續航因子/CD對升力的變化比升阻比對升力的變化更為敏感，無人機的續航因子將會隨升力的提高有一定幅度的增加。因此，將無人機單段機翼設計為兩段機翼后，其升力特性和巡航性能會有顯著提高［4-7］。

基于以上考慮，本文對某螺旋槳無人機的單段機翼進行了改進設計。在盡量保持原單段機翼幾何外形特征的前提下，通過二維翼型設計，將單段機翼改進為兩段機翼，并對翼身組合體進行流場數值模擬，通過與原無人機氣動性能比較評估，驗證了多段機翼應用于長航時無人機的工程價值。

2 氣動分析方法

由于本文主要對低速翼型和低速無人機的升力特性和阻力特性進行求解計算，粘性效應較為明顯，因此采用求解三維積分形式的非定常雷諾平均N-S方程組對翼型及翼身組合體氣動力特性進行分析評估。

為了驗證使用的數值計算方法的適應性，分別對GA(W)-1兩段翼型和HiLiftPW-1高升力翼身組合在給定狀態下進行流場求解并將結果與試驗數據進行比較。

算例1:對厚度及流動雷諾數比較接近的GA(W)-1兩段翼型進行流場求解［8］，其計算網格如圖1所示。圖2給出了帶有35°偏角的30%后緣襟翼的GA(W)-1翼型在 Ma=0.13，Re=1.5×106，α =10°時計算值與實驗值的比較。結果表明計算壓強分布與實驗值吻合良好，表明本文的方法能較準確地模擬二維粘性流動。

圖1 GA(W)-1翼型計算網格

圖2 GA(W)-1翼型計算值與實驗值對比

算例2:為了驗證本文中對三維低速流場計算方法的適應性，使用第一屆AIAA高升力研究的翼身組合體(HiLiftPW-1)進行驗證，其物面網格如圖3所示。

圖4和圖5分別給出了在Ma=0.2，Re=4.3×106條件下升力系數和阻力系數的計算值與實驗值的比較。計算結果與實驗結果吻合良好，表明流場求解方法可以作為低速三維粘性流場的求解工具。

圖3 HiLiftPW-1物面網格

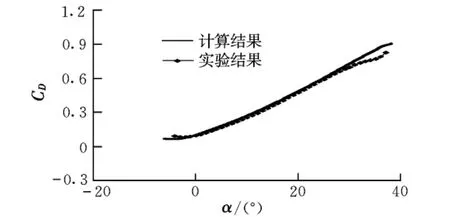
圖5 HiLiftPW-1阻力系數計算值與實驗值比較

3 兩段翼型設計方法及氣動特性分析

3.1 兩段翼型設計方法

本文的翼型設計是在前期單段翼型設計研究的基礎上，在保持原始翼型基本幾何特征的前提下，通過幾何方法切割出主翼和襟翼，再調整主翼和襟翼縫道搭配得到性能較好的兩段翼型。該方法最大的優點是能通過簡單的幾何手段，最大程度地體現原始翼型的幾何特征，快速高效地生成氣動性能良好的兩段翼型，并保證生成的兩段翼型在縫道處具有較高品質的流動。兩段翼型設計過程如圖6所示，更加詳細的步驟可參見文獻［9］。

圖6 兩段翼型設計過程

3.2 兩段翼型氣動特性

圖7和圖8分別給出了設計狀態Ma=0.15，Re=1.5×106下兩段翼型與原單段翼型升力系數及升阻特性的對比。從計算結果可以看出:本文所設計的兩段翼型的最大升力系數為2.72，最大升阻比為158.71，與原單段翼型相比最大升力系數增大了74.35%，最大升阻比增大了28.64%，最大升阻比對應的升力系數從1.1提高到2.0。計算結果表明:本文所設計的兩段翼型與原單段翼型相比，在提高升力的同時有效增大了翼型的升阻比，設計點升力系數提高明顯。設計結果表明，兩段翼型的氣動性能明顯優于單段翼型，符合本文的設計思路。下一步將把翼型以適當的方式組合成三維機翼并進行翼身組合體氣動特性分析評估。

圖8 翼型升阻比曲線對比

4 兩段機翼無人機氣動特性分析

為了進一步研究所設計得到的兩段翼型機翼的氣動特性，在原螺旋槳無人機上將單段機翼改裝為兩段機翼，無人機翼身組合體外形如圖9所示，物面網格如圖10所示。

圖11和圖12分別給出了設計狀態Ma=0.2，Re=2.9×106下兩段機翼無人機與原無人機的升力系數及續航因子的對比。從計算結果可以看出:最大升力系數由單段機翼無人機的1.48提高到2.38，增幅達到60.8%;最大續航因子從19提高到21;最佳巡航點對應的升力系數從1.1提高到1.8;兩段機翼無人機的可用升力系數從1.1持續到2.1，在該升力系數范圍內無人機皆可達到大于20的續航因子。

圖11 無人機升力系數曲線對比

圖12 無人機續航因子對比

從以上的對比分析可以看出，將傳統的單段機翼改進設計為兩段機翼，可以帶來更大的可用升力增量，顯著提高了無人機的升力特性。但是，升力的提高也將不可避免地帶來誘導阻力的增加，同時兩段機翼的寄生阻力也將更為明顯。阻力的增加抵消了升力增加對升阻比CL/CD的貢獻，因此兩段機翼的升阻比并沒有比單段機翼表現出明顯的優勢(見圖13);但在設計點CL=1.8附近，升力增加對續航因子C1.5

L/CD的增益比阻力增加對其的減損要大，因此，影響無人機航時的續航因子提高比較明顯(見圖12)。

圖13 無人機升阻比曲線對比

升力系數和續航因子的提高，可以減少無人機燃油消耗、增加留空時間。由于布雷蓋公式中各參數為非國際單位，故假定無人機在巡航狀態的各項參數為:η =0.8，c=0.67 lbs/(hp·hr)，σ =0.48，S=123.26 ft2，Wi=2 248 lbs，Wf=1 598 lbs，使用布雷蓋公式可以求得原單段無人機續航時間為25.95 h;相同巡航條件下，改進后的兩段機翼無人機的續航時間則為28.69 h，和單段無人機相比增加2.74 h。另外，設計點升力系數的提高還可以增大有效載荷、提升飛行高度、降低離地(落地)速度和縮短起飛(著陸)滑跑距離。

5 結束語

針對螺旋槳長航時無人機的使用設計要求，從現有單段翼型出發進行了高升力兩段翼型設計，結合某型螺旋槳無人機，對采用兩段翼型機翼的翼身組合體數模進行了氣動力特性數值分析。計算結果表明，將兩段機翼應用于螺旋槳無人機可以產生比單段機翼更大的可用升力和更高的續航因子，對無人機的續航時間、巡航高度、有效載荷以及起飛和著陸性能等都有較為明顯的改善，證明了本文設計思想和設計方法的可行性。

［1］ 世界無人機大全編寫組.世界無人機大全［M］.北京:航空工業出版社，2004:60-167.

［2］ Andrew H L，Eric L，Roland E F，etal.CU-24:Unmanned aerial vehicle design for long endurance［R］.AIAA-2009-208，2009.

［3］ 李珂.長航時無人機機翼平面參數及翼型選擇分析［J］.飛行力學，2007，24(3):9-11.

［4］ Alexander Nagel，Misha Shepshelovich.Development of high-lift UAV wings［R］.AIAA-2006-3467，2006.

［5］ Moshe Steinbuch，Misha Shepshelovich.Development of high altitude long endurance airfoils［R］.AIAA-2004-1052，2004.

［6］ David F Cerra，Joseph Katz.Design and evaluation of a high-lift，thick airfoil for UAV applications［R］.AIAA-2008-292，2008.

［7］ Steinbuch M，Marcus B，Shepshelovich M.Development of UAV wings— subsonic designs［R］.AIAA-2003-603，2003.

［8］ Wentz W H，Ostowari C.Additional flow field studies of the GA(W)-1 airfoil with 30-percent chord Fowler flap including slot-gap variations and cove shapemodifications［R］.NASA-CR-3687，1983.

［9］ 侯成義，龔志斌，劉城斌，等.高空長航時無人機高升阻比兩段翼型設計研究［J］.應用力學學報，2011，28(2):148-151.