壓擴(kuò)與預(yù)失真結(jié)合的峰均功率比抑制方法
李 鈾 張曉林 肖 鑫
(北京航空航天大學(xué) 電子信息工程學(xué)院,北京 100191)
近年來(lái),正交頻分復(fù)用(OFDM,Orthogonal Frequency Division Multiplexing)技術(shù)已經(jīng)廣泛應(yīng)用于現(xiàn)代移動(dòng)通信系統(tǒng)中.由于其突出的優(yōu)點(diǎn),航空航天領(lǐng)域也將其列為研究的熱點(diǎn)技術(shù).但是,OFDM信號(hào)的高峰均比,成為其應(yīng)用在航空航天領(lǐng)域的主要障礙.要減弱峰均比帶來(lái)的不利影響,通常有兩個(gè)辦法:
1)降低信號(hào)的峰均功率比(PAPR,Peak to Average Power Ratio);
2)對(duì)功率放大器進(jìn)行線性化處理,減少功放非線性帶來(lái)的干擾.
壓擴(kuò)變換方法是一種簡(jiǎn)單有效的降低OFDM信號(hào)峰均比的辦法.由于不會(huì)受到信號(hào)調(diào)制方式以及子載波數(shù)量的限制,而且降低峰均比效果明顯,受到了學(xué)者們的廣泛關(guān)注[1-3].在功放線性化方法中,預(yù)失真法由于其可以和現(xiàn)代DSP(Digital Signal Processing)技術(shù)相結(jié)合,顯示出很好的發(fā)展前景,也受到了越來(lái)越多的重視.
在以往的文獻(xiàn)中,壓擴(kuò)和預(yù)失真是作為單獨(dú)的技術(shù)進(jìn)行研究的.本文將把二者結(jié)合在一起,提出一種壓擴(kuò)與預(yù)失真相結(jié)合的OFDM信號(hào)峰均比抑制方法.
1 壓擴(kuò)變換
壓擴(kuò)變換法是一種預(yù)畸變的降低峰均比的方法,其基本原理是對(duì)大信號(hào)進(jìn)行壓縮,對(duì)小信號(hào)進(jìn)行擴(kuò)大,以降低信號(hào)的峰值并保持信號(hào)的平均功率基本不變,來(lái)達(dá)到降低信號(hào)峰均比的目的.最簡(jiǎn)單的壓擴(kuò)變換為線性對(duì)稱壓擴(kuò)變換(LST,Linear Symmetrical Transform)[1],設(shè)變換前的信號(hào)的幅度為r(t),變換后的信號(hào)為r'(t),則有
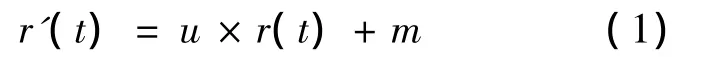
式中,0<u≤1;0≤m≤max(r(t)).參數(shù) u用來(lái)壓擴(kuò)的程度,m用來(lái)控制壓縮與擴(kuò)大的分界點(diǎn),如圖1所示.
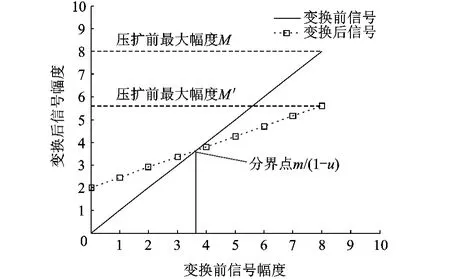
圖1 線性壓擴(kuò)原理圖
LST實(shí)現(xiàn)簡(jiǎn)單,且對(duì)OFDM信號(hào)峰均比的抑制效果明顯,但由于其采用令信號(hào)失真的預(yù)畸變方法,增加了通信過(guò)程中的噪聲,降低了信噪比,從而使誤碼率性能惡化.文獻(xiàn)[1]分析了幾種常見(jiàn)的壓擴(kuò)變換方法,給出了LST的峰均比抑制性能及誤碼率特性,如圖2所示.根據(jù)作者分析,參數(shù)u對(duì)誤碼率有明顯的影響,而參數(shù)m對(duì)誤碼率沒(méi)有影響.從圖中可知,參數(shù)u越大,抑制峰均比性能越好,誤碼率性能越差;反之,抑制峰均比性能越差,誤碼率性能越好.
信號(hào)經(jīng)過(guò)壓擴(kuò)變換后,要經(jīng)過(guò)功率放大器及信道后才能到達(dá)接收端,因此在研究系統(tǒng)性能時(shí),還要加入功放非線性及信道的影響.文獻(xiàn)[1-3]在研究中并沒(méi)有考慮到功放非線性的因素.在下一節(jié)中,本文將討論功放非線性對(duì)系統(tǒng)性能的影響.由于篇幅原因,本文中只考慮AWGN(Additive White Gaussion Noise)信道.
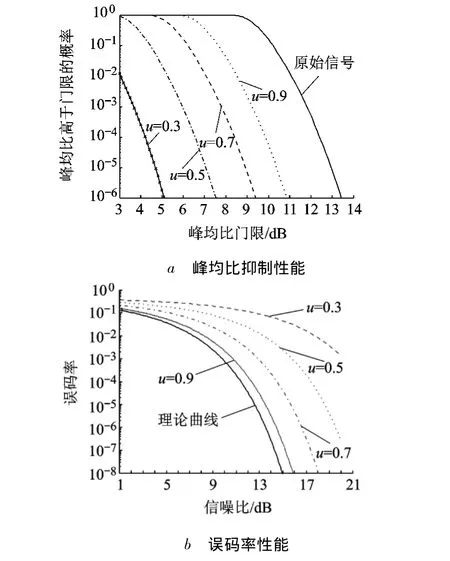
圖2 LST的峰均比抑制性能及誤碼率性能
2 功率放大器非線性
2.1 功率放大器非線性模型
最常見(jiàn)的功率放大器非線性模型是Saleh模型[4],它被用來(lái)描述行波管放大器(TWTA,TravelingWave Tube Amplifier)的非線性特性,TWTA是衛(wèi)星通信系統(tǒng)中重要的高功放元件.
Saleh模型的具體形式如下:
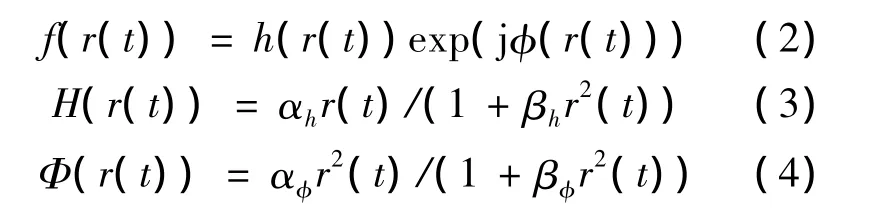
式中,H(r(t))描述了AM/AM(Amplitude Modulation/Amplitude Modulation)失真特性;Φ(r(t))描述了AM/PM(Amplitude Modulation/Phase Modulation)失真特性.
2.2 功率放大器非線性對(duì)誤碼率影響
在衛(wèi)星系統(tǒng)中,由于能源有限功率放大器工作在高效率模式下,因此有很強(qiáng)的非線性.功放的非線性會(huì)引起信號(hào)的帶內(nèi)和帶外噪聲.帶外噪聲主要影響相鄰頻段的信號(hào),且可以通過(guò)濾波器去除.而帶內(nèi)噪聲無(wú)法濾除,會(huì)降低系統(tǒng)的誤碼率性能.已經(jīng)有大量學(xué)者研究了經(jīng)過(guò)功放后,信號(hào)的統(tǒng)計(jì)特性.在文獻(xiàn)[5]中,作者利用Bussgang定理推導(dǎo)出OFDM信號(hào)經(jīng)過(guò)功放后的信噪比特性.Bussgang定理給出了實(shí)值函數(shù)形式的功放輸入信號(hào)和輸出信號(hào)的關(guān)系[6]
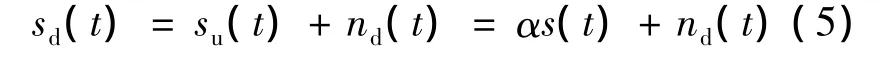
式中,s(t)和sd(t)分別為功放的輸入和輸出信號(hào);α為衰減系數(shù);nd(t)為噪聲信號(hào),且nd(t)與s(t)統(tǒng)計(jì)不相關(guān).當(dāng)功放由Saleh模型給出,則有sd(t)=f(r(t))=h(r(t))exp(jφ(r(t)))(6)
當(dāng)功放的輸入和輸出為復(fù)信號(hào)時(shí),輸出信號(hào)的自相關(guān)函數(shù)[5]為
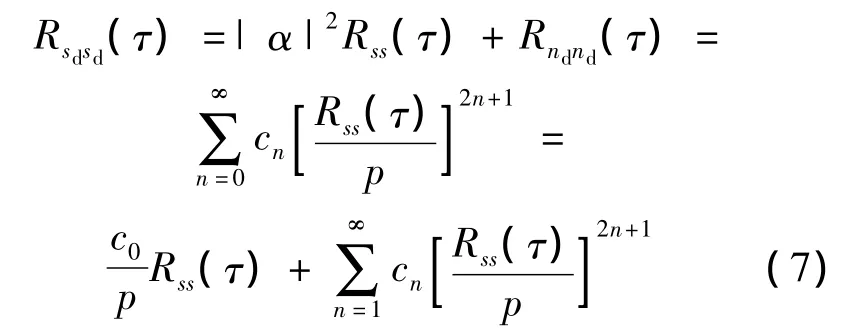
式中,Rss(τ)為輸入復(fù)信號(hào)的自相關(guān)函數(shù);Rndnd(τ)為功放引入的噪聲;p為輸入信號(hào)平均功率;系數(shù)cn的計(jì)算方法如下式:
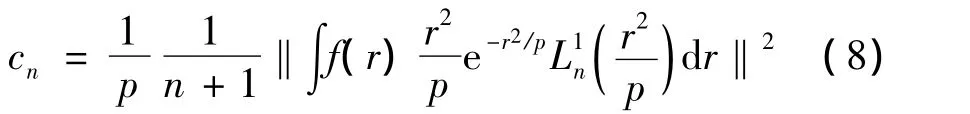
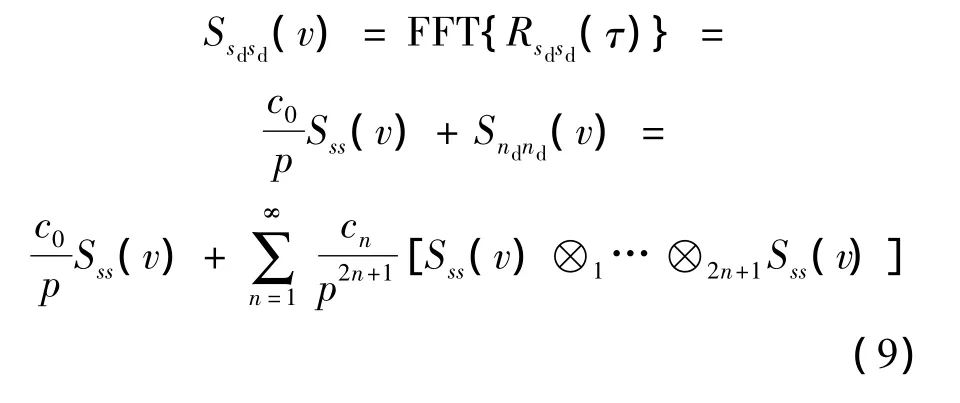
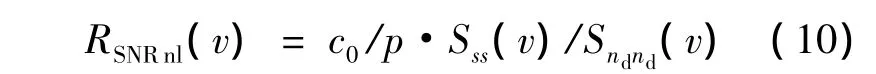
系統(tǒng)的視在信噪比為
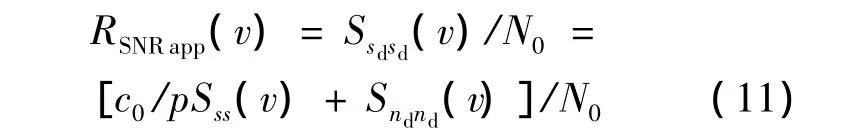
此時(shí)的有效信噪比為
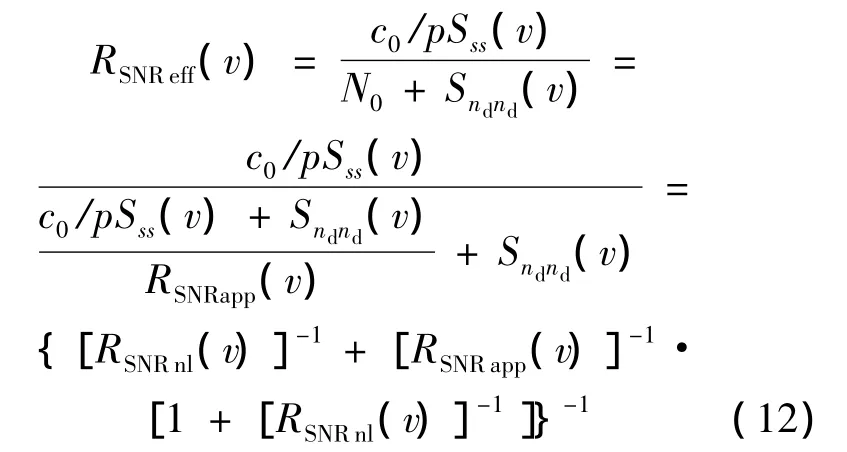
當(dāng)功放的輸入為OFDM信號(hào)時(shí),式(10)~式(12)中v的取值為發(fā)送有用信息的子載波數(shù).而且,根據(jù)OFDM所采用的調(diào)制階數(shù),分別計(jì)算每路子載波的誤碼率,最后將各路子載波的誤碼率進(jìn)行平均(設(shè)有用信號(hào)的子載波數(shù)目為L(zhǎng)data),得到系統(tǒng)的誤碼率:

由式(10)~式(12)可知,功放非線性引入的噪聲會(huì)對(duì)信號(hào)的信噪比產(chǎn)生影響.圖3仿真了采用LST后的信號(hào),經(jīng)過(guò)功放后的誤碼率情況,這里的功放選用Saleh模型來(lái)描述,系數(shù)cn取n=0,1,…,5.比較圖3與圖2,可得經(jīng)過(guò)功放后,當(dāng)參數(shù)u取不同值時(shí),系統(tǒng)誤碼率性能都變差了.
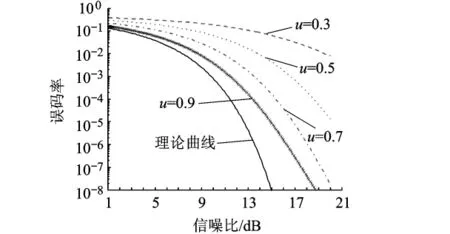
圖3 線性壓擴(kuò)經(jīng)過(guò)功放后誤碼率性能
3 預(yù) 失 真
預(yù)失真(PD,Pre-Distortion)可以削弱功放的非線性特性,但不能將其完全消除.當(dāng)功放非線性為Saleh模型時(shí),理想PD可以完全消除功放的AM/PM失真,殘留部分AM/AM失真.其非線性模型表現(xiàn)為一個(gè)軟限幅器[7]:
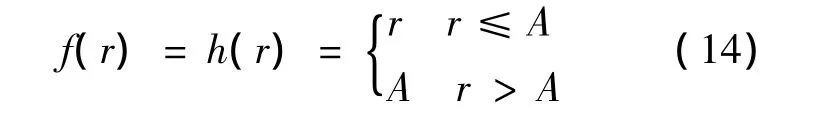
式中,A為限幅后幅度的最大值,這里假設(shè)理想PD為單位增益.將式(14)代入式(8),參考數(shù)學(xué)手冊(cè)[8],經(jīng)過(guò)推導(dǎo)后得到參數(shù)cn的計(jì)算方法:
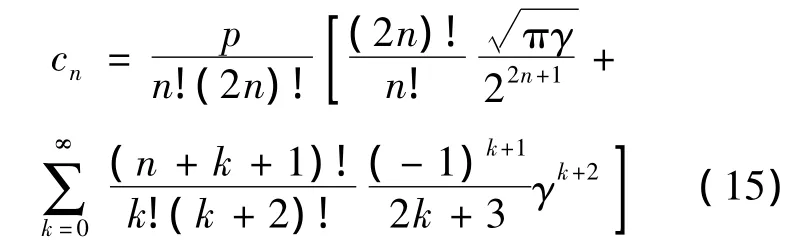
式中,γ定義為功放的輸入功率回退IBO(Input Back-Off),可用下式表示:

將式(15)代入式(12),可以得出信號(hào)經(jīng)過(guò)理想PD后,各子載波的信噪比,進(jìn)而得到系統(tǒng)的誤碼率.圖4仿真了系統(tǒng)誤碼率與γ之間的關(guān)系,從圖中可以看到γ越大,RBER越好.
IBO表征了功放的工作狀態(tài):IBO越大,表明功放的工作區(qū)域越接近線性放大區(qū)間,功放的效率越低,功放的非線性越小,從而系統(tǒng)的BER越好;反之,功放的工作區(qū)域越接近飽和,功放的效率越高,功放的非線性越大,從而系統(tǒng)的BER越差.
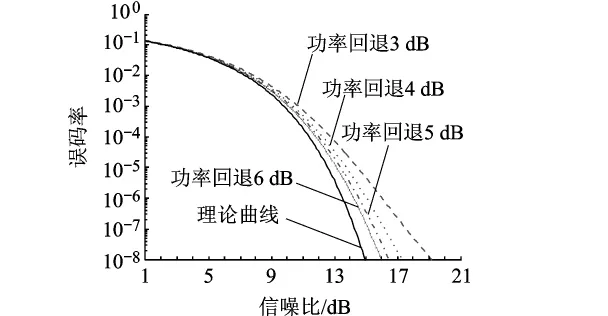
圖4 不同功率回退下誤碼率性能
4 壓擴(kuò)與預(yù)失真聯(lián)合分析
從上面的分析可知,LST的誤碼率性能與參數(shù)u成正比,而抑制峰均比的性能與參數(shù)u成反比.而當(dāng)系統(tǒng)中存在功放和PD時(shí),誤碼率性能不僅僅和參數(shù)u有關(guān),還跟功放的非線性參數(shù)及理想PD的功率回退有關(guān).本節(jié)將把壓擴(kuò)與PD結(jié)合起來(lái),分析系統(tǒng)的誤碼率性能進(jìn)而對(duì)原有的LST方法進(jìn)行改進(jìn).
首先,將第1節(jié)中的LST公式修改如下:
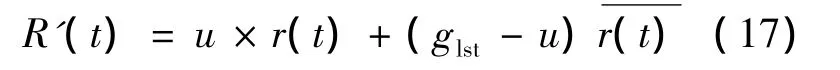
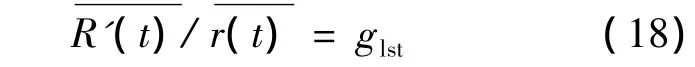
然后,利用文獻(xiàn)[1]的方法修改式(12)得到信號(hào)子載波有效信噪比的計(jì)算方法如下:
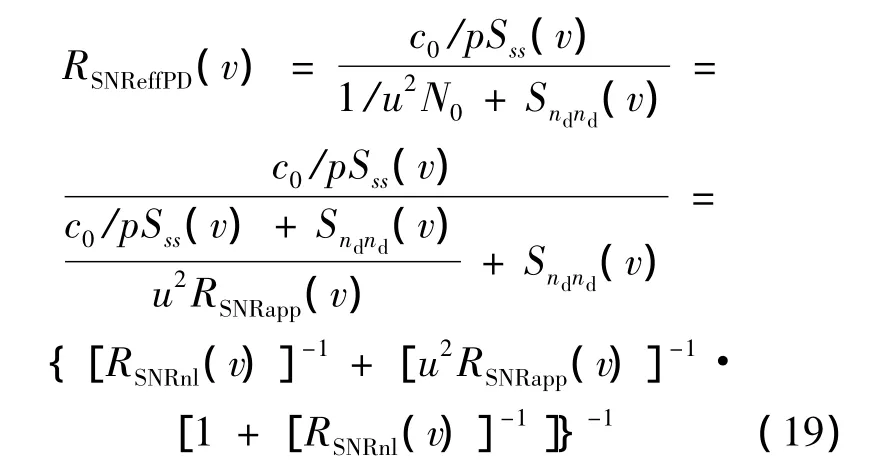
其中參數(shù)cn用式(15)來(lái)計(jì)算.然后,用式(19)與式(13)進(jìn)行計(jì)算,得出系統(tǒng)的誤碼率.
圖5顯示了仿真結(jié)果,這里選擇功放的IBO,γ=3 dB,參數(shù) u 選擇 0.9 和 0.7,參數(shù) glst選擇1.25和0.95.從圖5 中可得,當(dāng)參數(shù) glst固定時(shí),參數(shù)u越大誤碼率越好;當(dāng)參數(shù)u固定時(shí),參數(shù)glst越大誤碼率越好.并且,注意到當(dāng)RSNRapp>18 dB后,參數(shù) u=0.7,glst=1.25 時(shí)的信噪比門限,較參數(shù) u=0.9,glst=0.95 時(shí)改善0.8 dB.同時(shí),與圖3相比較,當(dāng)參數(shù)u=0.9時(shí)相同誤碼率對(duì)應(yīng)的信噪比門限改善2 dB左右.
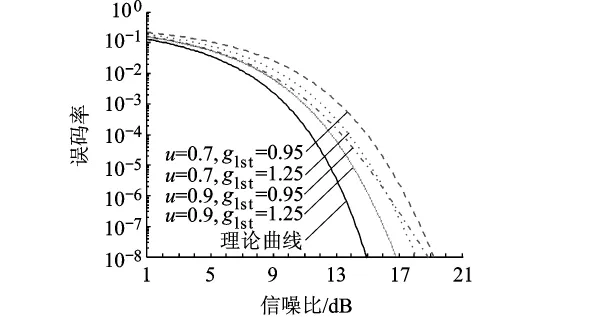
圖5 功率回退3 dB時(shí)誤碼率與參數(shù)u和g lst關(guān)系
因此,本文提出的LST改進(jìn)方法為,在系統(tǒng)中存在功放和PD時(shí),用兩個(gè)參數(shù)來(lái)抑制PAPR.通過(guò)減小參數(shù)u來(lái)改善PAPR,通過(guò)增大參數(shù)glst來(lái)糾正由減小參數(shù)u帶來(lái)的系統(tǒng)誤碼率的下降.
5 結(jié)論
本文通過(guò)對(duì)功率放大器非線性效應(yīng)和理想預(yù)失真的分析,得出以下結(jié)論:①在研究壓擴(kuò)方法的誤碼率性能時(shí),不能忽略功放非線性的影響.功放非線性會(huì)增加系統(tǒng)的噪聲,從而降低系統(tǒng)的誤碼率.②將LST方法改進(jìn)后再結(jié)合預(yù)失真方法,與原有的LST方法比,增加了一個(gè)可以控制誤碼率性能的參數(shù),從而比原有方法具有更高的靈活度.仿真結(jié)果證明,本方法性能有所提高.
References)
[1] Huang Xiao,Lu Jianhua,Zheng Junli,et al.Companding transform for reduction in peak-to-average power ratio of OFDM signals[J].IEEE Transactions on Wireless Communications,2004,3(6):2030 -2039
[2] Jeng Shiann-Shiun,Chen Jia-Ming.Efficient PAPR reduction in OFDM systems based on a companding technique with trapezium distribution [J].IEEE Transactions on Broadcasting,2011,57(2):291-298
[3] Aburakhia SA,Badran E F,Mohamed D A E.Linear companding transform for the reduction of peak-to-average power ratio of OFDM signals[J].IEEE Transactions on Broadcasting,2009,55(1):155-160
[4] Saleh A.Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers[J].IEEE Transactions on Communications,1981,29(11):1715 -1720
[5] Banelli P,Cacopardi S.Theoretical analysis and performance of OFDM signals in nonlinear AWGN channels[J].IEEE Transactions on Communications,2000,48(3):430 -441
[6] Papoulis A.Probability,random variables and stochastic process[M].Third edition.New York:McGraw-Hill,1991:307 -308
[7] Kaye A R,George D A,Eric M J.Analysis and compensation of bandpass nonlinearities for communications[J].IEEE Transactions on Communications,1972,20(5):965 -972
[8] Prudnikov A P,Brychkov Yu A,Marichev O I.Integrals and series[M].New York:Gordon and Breach,1986:457 -475

