例談學生數(shù)學作圖分析能力培養(yǎng)的策略

滕衍文

數(shù)學問題常以文字形式呈現(xiàn)，且表述比較抽象. 教學中，筆者發(fā)現(xiàn)大多數(shù)學生解決問題沒有形成一定的策略方法，更不會根據(jù)題目的特征靈活地作圖分析，使問題迎刃而解. 筆者結合教學實踐，談談培養(yǎng)學生數(shù)學作圖分析能力的具體策略，以提高學生的解題能力.

一、數(shù)學作圖分析的內(nèi)涵

數(shù)學作圖分析的內(nèi)涵是指在小學數(shù)學教學中教師從學生已有的生活經(jīng)驗和知識背景出發(fā)，結合所學內(nèi)容的特征，組織學生進行數(shù)學作圖分析的實踐活動，使學生通過作圖分析有效地解決數(shù)學實際問題，發(fā)展學生的空間觀念，提高學生的解題能力，培養(yǎng)學生的思維能力.

二、數(shù)學作圖分析的基本方法

（１）示意法：就是以圖示意和解意，采用各種簡明符號傳遞信息，用以標示各種數(shù)學圖形或數(shù)量關系的信息，以便于學生簡明地尋找到問題解決的一種方法. 如：和倍問題、和差問題等，可以引導學生畫線段圖幫助分析數(shù)量關系，利于解決問題.

（２）尺規(guī)法：就是用簡單的直尺和圓規(guī)按要求作圖，構成標準、規(guī)范、清晰、美觀的數(shù)學圖形，便于學生準確地分析解決問題的方法. 如：讓學生畫一個直徑為５厘米，高為３厘米的圓柱平面展開圖，并算出表面積. 學生運用直尺和圓規(guī)，先做圖，后計算，在作圖中掌握了“表面積”的概念本質(zhì).

（３）縮放法：把一個數(shù)學平面圖形按一定的比例進行縮小或放大. 如一個長方形長是８厘米，寬是５厘米. 分別把它按２ ∶ １放大，１ ∶ ２縮小. 畫出放大、縮小后的圖形.

（４）平移旋轉法：將一個數(shù)學平面圖形按要求進行平移或旋轉，得到一個新的圖形，從而使問題得解.

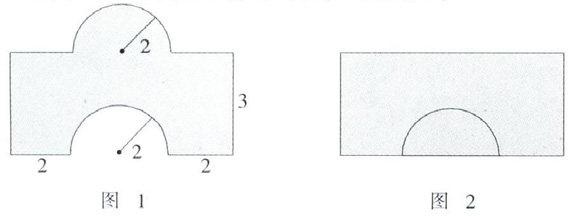
如：求圖1中陰影部分的面積（單位：厘米）.

思路解析：圖1是個不規(guī)則的圖形，如果把上面的半圓平移至下半圓空白處，這個不規(guī)則圖形就轉化成了一個長方形（如圖2）. ８ × ３ ＝ ２４（平方厘米）.

（５）割補法：將一個數(shù)學平面圖形按要求進行割補，巧妙得到解決問題的途徑.

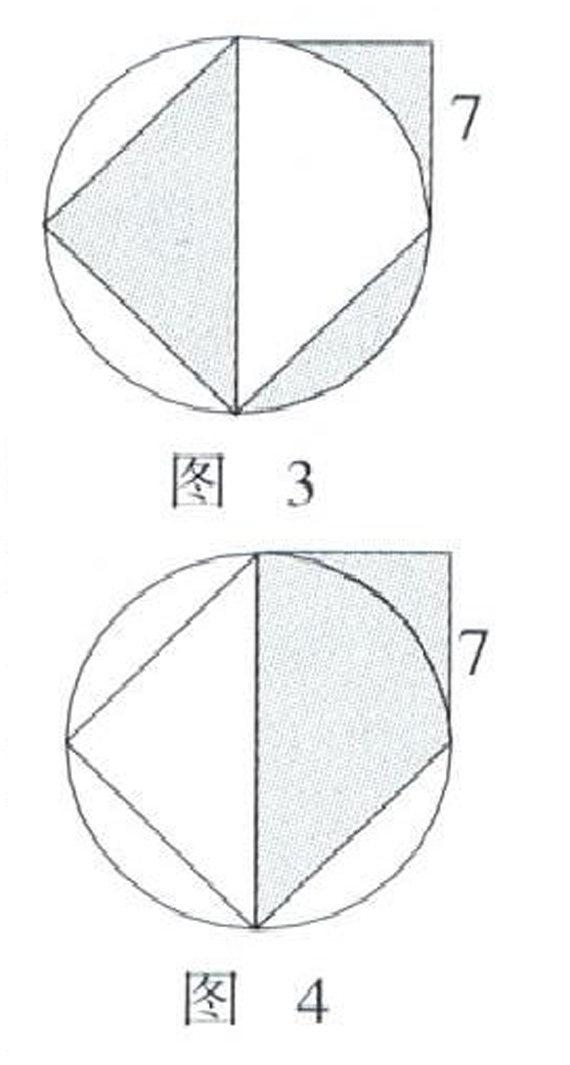
如：求圖3中陰影部分的面積（單位：厘米）.

思路解析：如將三個部分的陰影部分面積分別算出來，再相加，可以求出，但很繁瑣. 此題運用兩次翻轉，可將三處陰影部分拼成一個直角梯形，則求陰影部分的面積，只需求出直角梯形的面積（如圖4）.

（７ × ２ ＋ ７） × ７ ÷ ２ ＝ ７３．５（平方厘米）.

（６）軟件法：根據(jù)內(nèi)容的需要借助作圖軟件進行數(shù)學作圖的方法. 常用于較復雜圖形的精確作圖. 如：幾何畫板、數(shù)學圖像描繪器、數(shù)碼手繪等.

三、學生數(shù)學作圖分析能力培養(yǎng)策略的實施

１. 激發(fā)學生學習興趣，培養(yǎng)學生作圖分析的觀念

著名教育家蘇霍姆林斯基曾說過：“如果教師不想方設法讓學生進入情緒高昂和智力振奮的內(nèi)心狀態(tài)，就急于傳授知識，那么這種知識只能使人產(chǎn)生冷漠的狀態(tài)，而不動感情的腦力就會帶來疲倦. ”

如教學“倍數(shù)問題”：有５筐梨子，每筐梨子的只數(shù)相同，從每一筐中各拿出７５只，剩下的梨剛好是原來兩筐梨的只數(shù). 問：原來每筐有梨子多少只？

思路解析：按一般的思考方法不大容易解答出來，可以從條件的反面去思考，抓住“剩下的梨剛好是原來兩筐梨的只數(shù)”讓學生作圖分析，聯(lián)想出它的反面：拿出的（７５ × ５）只數(shù)剛好是原來３筐的只數(shù).

７５ × ５ ÷ （５ － ２） ＝ ３７５ ÷ ３ ＝ １２５（只）.

這樣的教學，學生通過作圖分析，化抽象為直觀，喚醒學生潛在的動力，使學生對數(shù)學作圖分析活動產(chǎn)生興趣.

２. 教師示范引領作圖，指導學生作圖分析的方法

問題的解決包括一系列的操作，對小學生而言，作圖分析需要教師的示范引領. 在教學中，教師要根據(jù)教學需要，正確指導學生進行有目的的作圖分析，并與觀察、語言及思維表達相結合，促使學生數(shù)學作圖分析方法的形成. 如：畫一個周長為１８．８４厘米的圓，再求出圓的面積. 教師應引導學生選擇作圖的方法，即尺規(guī)法. 先算出半徑１８．８４ ÷ ３．１４ ÷ ２ ＝ ３（厘米），再用尺規(guī)確定半徑的長度，畫出圓，算出面積. 作圖教學中重要的是幫助學生建立作圖思路，形成作圖方法.

３. 有效設計作圖活動，訓練學生作圖分析的能力

蘇霍姆林斯基有句名言：“兒童的智慧在他的手指尖上. ”數(shù)學作圖分析活動是一種特殊的認知活動，一方面它是學生手與眼協(xié)同活動，對客觀事物的動態(tài)感知過程；另一方面，它又是學生手與腦密切溝通，把外部動作形態(tài)轉化為內(nèi)部語言形態(tài)的智力內(nèi)化方式. 教學中有效設計作圖活動，能使學生加深對數(shù)學知識的理解，發(fā)現(xiàn)知識的內(nèi)在聯(lián)系，更好地獲取新知識.

如：蘇教版六年級數(shù)學上冊“解決問題的策略”，例題１：小明把７２０毫升果汁倒入６個小杯和１個大杯，正好都倒?jié)M，小杯的容量是大杯的三分之一. 小杯和大杯的容量各是多少毫升？題中的數(shù)量關系復雜抽象，學生理解不透徹. 教學時，筆者設計了一張畫有例題已知條件的圖，每個小組一張，讓學生在小組內(nèi)作圖進行替換. 學生借助圖形的直觀作用，通過畫一畫、寫一寫、說一說，理解了題目中的數(shù)量關系 ，將復雜的抽象思維轉化為簡單的形象思維，易使學生建構解題思路，掌握替換的方法.

４. 開展作圖分析評價，提高學生作圖分析的創(chuàng)新品質(zhì)

學生在作圖過程中，定會出現(xiàn)各種問題，課堂教學中要預留時間，組織學生開展作圖分析評價. 經(jīng)常給學生提供作圖分析的展示與評價的機會，讓學生間的心得、經(jīng)驗、方法適時碰撞、吸納，在數(shù)學作圖分析中學生便會迸發(fā)出創(chuàng)新思維的火花，更能有效地提高學生數(shù)學作圖分析的創(chuàng)新思維品質(zhì).

學生數(shù)學作圖分析能力的培養(yǎng)需要一個循序漸進的過程，教師只有在教學實踐中結合教學內(nèi)容的特點，有的放矢，系統(tǒng)訓練，才能使學生掌握方法，自覺運用，有效提高學生的解題能力.