永磁同步電機在線多參數辨識方法研究

劉 亢，劉忠途，李樂榮，宗志堅

(中山大學，廣東廣州510006)

0 引 言

目前針對永磁同步電動機伺服系統調速控制較為成熟的方法主要有兩種［1］:矢量控制和直接轉矩控制。矢量控制策略中電流環響應速度遠大于轉速環，電流環控制器參數的設定直接左右整個控制系統的性能，而電機定子參數(定子電阻與電感)對電流環控制器設計影響最大，速度環控制器參數的整定也受到電流環控制器參數設計的影響，同樣離不開定子參數的辨識;直接轉矩控制策略中將電磁轉矩與定子磁鏈矢量作為控制變量，對定子磁鏈矢量的準確估計十分關鍵，而定子磁鏈矢量估計是否正確取決于永磁電機參數的精確辨識。對于現代永磁同步電動機控制的其它方法，如弱磁控制、最小損耗控制、自適應控制等也依賴于電機參數的精確辨識［2－4］。

由于永磁同步電動機系統多變量、非線性、強耦合的特點，在實際應用中往往需要同時用到多個參數，如果能夠找到一種算法簡單且能夠快速同時辨識多個電機參數的方法，對于電機控制精度的提高與電機運行狀態的準確監視具有重大意義。國內外諸多學者對電機多參數辨識策略進行了研究。文獻［5］運用EKF(擴展卡爾曼濾波)法完成了內埋式永磁同步電動機永磁磁鏈的在線辨識，但其假定系統噪聲及測量噪聲已知且算法較為復雜。文獻［6］借助POPOV超穩定理論建立了永磁同步電動機的參數辨識模型，保證了系統穩定性與參數收斂性，參考模型、電壓模型中包含有純積分環節，影響辨識結果，算法較EKF更為復雜。文獻［7］將帶遺忘因子最小二乘方法應用于定子電阻、定子繞組電感與永磁體磁鏈的在線辨識，但是辨識過程中需周期性階躍改變q軸電流，實用價值不高。文獻［8］把多新息最小二乘法引入到感應電機參數辨識中來，但其未加入遺忘因子對協方差矩陣進行更新，跟蹤精度不高。

本文采用帶遺忘因子的多新息最小二乘法，對面裝式永磁同步電動機進行在線參數辨識，該方法僅利用定子電壓、電流信號和轉速信號，減少了其它因素干擾;多新息方法可以抑制壞數據對參數辨識的影響，具有較強的魯棒性，而合理選擇遺忘因子對協方差矩陣可進行更新，可以加速辨識參數的收斂。仿真結果表明辨識具有較好收斂性、魯棒性與較高精度。

1 多新息最小二乘法

最小二乘法又稱最小平方法，通過最小化誤差的平方和來尋找模型的最佳函數匹配。目前，最小二乘法在系統辨識領域應用廣泛，在許多方法失效的情況下，最小二乘法依然能夠簡單有效的解決問題。但同時最小二乘法有一些缺陷:最小二乘估計結果保持無偏性、一致性的前提是系統干擾為均勻白噪聲，但很多情況下系統干擾充滿隨機性;運算過程中伴隨數據量的增長，算法易出現數據飽和現象。針對這些缺陷，中外學者提出了一些改進算法［9］，如遞推最小二乘法、相關分析最小二乘法、增加輔助變量法、增廣矩陣法等。本文將多新息辨識方法［10］同最小二乘法相結合，通過新息矩陣與遺忘因子來修正最小二乘法。

考慮下列時變系統:

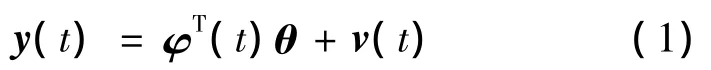
式中:θ為系統的時變參數向量，y(t)∈R1為系統輸出，u(t)∈R1為系統輸入，φ(t)∈Rn是由系統輸入輸出數據(y(t－1)，u(t－1)，y(t－2)，u(t－2)，…)構成的新息向量，v(t)∈R1為系統受到的噪聲向量。

估計參數θ的最小二乘算法可表示:

式中:e(t)=y(t)－φT(t)θ(t－1)為標量新息;L(k)∈Rn為增益向量。e(t)作為標量新息代表迭代過程中單步的新息，稱為單新息(single－innovation)。將單新息e(t)加以推廣，發展成為多新息辨識方法［11］，它是通過新息向量 E(p，t)∈Rp，即多新息(multi－innovation)來進行參數辨識。多新息E(p，t)包括了迭代過程中p步的新息，同樣將輸出向量y(t)擴展為累積輸出向量Y(p，t)，將新息向量φ(t)擴展為累積新息矩陣φT(p，t)，將噪聲向量v(t)擴展為噪聲矩陣V(p，t)。定義如下:

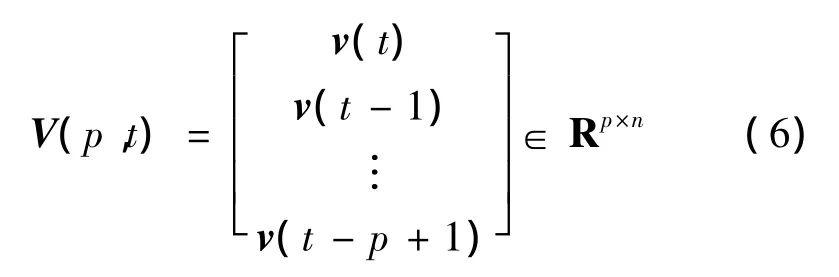
此時可以得到系統的多新息辨識模型:

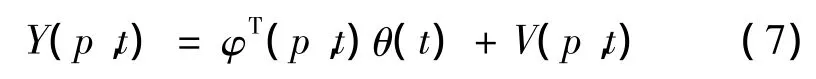
引入遺忘因子對協方差矩陣進行更新，估算系統多新息模型參數向量θ(t)的最小二乘法表示如下:

P(t)為協方差矩陣。

在跟蹤時變參數時，多新息最小二乘法也一樣存在數據飽和的問題。選擇合適的遺忘因子λ，用于更新協方差矩陣P(t)，以降低過去測量值的比重，增加當前測量值的比重，以減小數據飽和問題對辨識系統的影響。

當多新息p=1時，該算法就退化為遞推最小二乘辨識算法(RLS)，所以說多新息最小二乘法是RLS的一種推廣，通過多新息的引用，能夠抑制壞數據的影響，提高參數估計精度并具有較強魯棒性。

2 永磁同步電動機動態模型

永磁同步電動機采用永磁體轉子進行勵磁，不加入勵磁繞組及直流勵磁電源，省去勵磁損耗，提高了電機效率與功率密度;取消了容易出問題的電刷與集電環，使結構更為簡單，運行更為可靠。正弦波永磁同步電動機于d－q坐標系建立數學模型，不僅可以分析電機的穩態運行性能，也可用于分析電機的瞬態性能。

在建立永磁同步電動機d－q軸數學模型之前對電機本體及外界影響做出一些假設［12］，永磁同步電動機的電壓方程式:

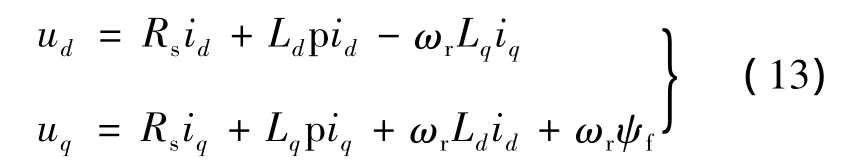
機械運動方程式:

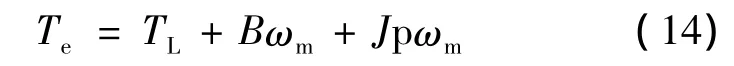
方程中各量均為瞬態值。ud、uq為定子繞組的d、q軸電壓;id、iq為定子繞組的 d、q軸電流;ωr為電氣角速度;p為極對數;ωm為機械角速度Ld、Lq為定子繞組的d、q軸電感;Rs為定子相電阻;ψf為永磁體產生的磁鏈;J為轉動慣量(包括轉子轉動慣量與負載折算的轉動慣量);Te為電機電磁轉矩;TL為負載轉矩;B為運動阻尼系數;p為微分算子。

3 永磁同步電動機多參數辨識

為了應用多新息最小二乘法(MILS)，需要對永磁同步電動機轉子坐標系下電壓方程式(13)進行離散化。由于本文選擇R、L、ψf為辨識對象，因此僅需對q軸電壓方程進行離散。對于面裝式永磁同步電動機Ld=Lq=L，取足夠小的采樣時間Ts，那么:

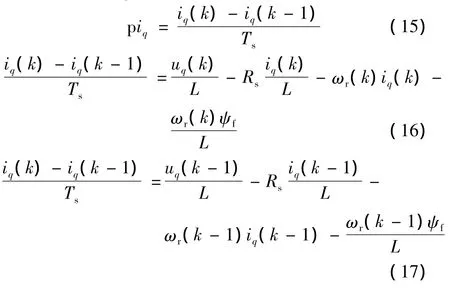
由式(16)、式(17)即可得永磁同步電動機離散動態方程:

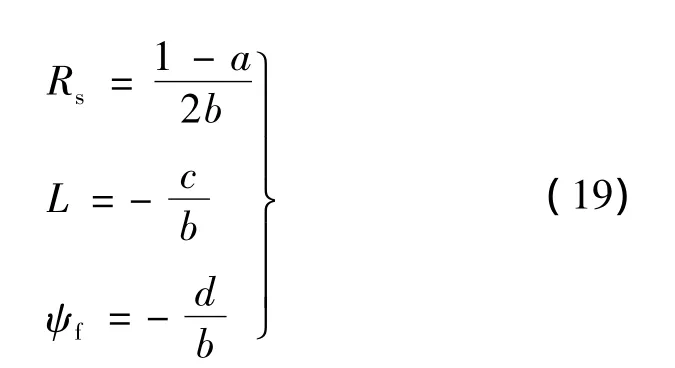
從而可以利用多新息最小二乘法對Rs、L、ψf進行在線辨識，對應于算法模型:

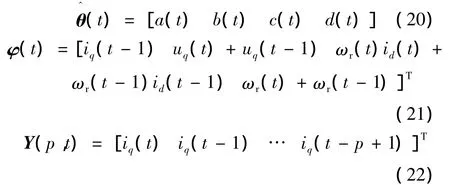
綜上可知，僅需要檢測定子電壓、電流、轉速信號即可估算出定子電阻、電感與轉子永磁體磁鏈，易于工程實現。

4 辨識系統仿真分析

在MATLAB/Simulink中建立仿真系統如圖1所示。控制系統采取速度、電流雙閉環控制;控制策略選用經典的id=0策略。模型中永磁同步電機參數:額定功率PN=1.2 kW，額定轉速nN=3 000 r/min，額定轉矩 TN=4 N·m，定子電阻 Rs=1.05 Ω，電感 L=3.28 mH，轉子永磁體磁鏈 ψf=0.133 Wb，極對數 p=4，轉子慣量J=0.54 ×10－3kg·m2，轉矩系數KT=0.8 N·m/A。給定轉速nref=300 r/min，電機負載為恒扭矩TL=1 N·m。

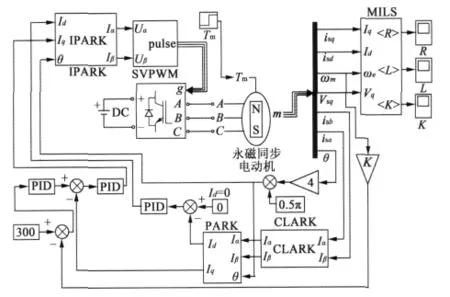
圖1 矢量控制系統框圖

通過S－Function建立MILS辨識模塊，通過對電機電壓、電流、轉速信號的采樣，經離散化后進行多新息最小二乘法迭代，仿真步長Ts=1×10－5s，仿真系統運行1 s，多新息長度分別取p=1(相當于RLS)、p=3以作比較，遺忘因子 λ=0.999 5。圖2至圖4顯示了各參數在不同多新息長度下的收斂過程。

電感真實值L=3.28 mH，辨識結果如圖2所示。

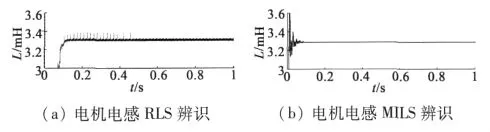
圖2 電感辨識

永磁體磁鏈真實值ψf=0.133 Wb，辨識結果如圖3所示。

圖3 磁鏈辨識

電機定子電阻Rs=1.05 Ω，辨識結果如圖4所示。

圖4 定子電阻辨識

從圖2～圖4可以看出，多新息最小二乘法的實驗結果較好地收斂于電機參數的真實值。與傳統的RLS辨識方法相比，MILS辨識響應更快，波動更小，精度更高。

為驗證算法的魯棒性，以磁鏈辨識為例。設定電機負載階躍變化，初始TL=1 N·m，加載TL=4 N·m，辨識結果如圖5所示。

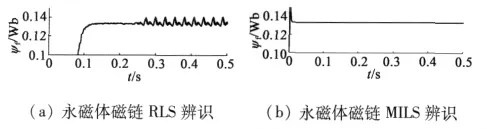
圖5 階躍負載下永磁體磁鏈辨識

從圖5中可以明顯看出，RLS辨識方法在階躍負載輸入時波動較大，甚至短時間內無法收斂;而MILS辨識方法幾乎沒有受到影響。這說明多新息方法相比于單新息方法具有先天的優勢，由于多新息的采用削弱了外界干擾及壞數據的影響，具有較強的魯棒性。

5 結 語

本文介紹了一種永磁同步電動機的在線多參數辨識方法，根據易于采集的定子電壓、電流、轉速信號，利用多新息最小二乘法(MILS)下的辨識模型估算出電機的定子電阻、電感與永磁體磁鏈。

仿真結果表明:通過多新息的引入，提高了辨識收斂性、削弱了辨識的波動;加入遺忘因子對協方差矩陣進行更新，避免了因數據飽和造成的一系列問題;辨識結果更為準確，適用于永磁同步電動機自適應控制、實時狀態監測的高精度場合，具有重要意義。

［1］吳衛安.永磁同步電機調速系統研究［M］.武漢:華中科技大學，2007.

［2］李高林.基于電動車的永磁同步電機的弱磁控制［J］.電力電子技術，2010(6):88－89.

［3］Rongmin C.Low －speed performance research for permanent magnet synchronous linear motor based on nonparametric model learning adaptive control［C］//2011 International Conference on Electrical Machines and Systems.2011:1 －5.

［4］王曉磊，趙克友.永磁同步電機最小損耗的直接轉矩控制［J］.電機與控制學報，2007(4):331－334.

［5］史宇超.內埋式永磁同步電機永磁磁鏈的在線辨識［J］.電工技術學報，2011(9):48－53.

［6］安群濤，孫力，趙克.一種永磁同步電動機參數的自適應在線辨識方法［J］.電工技術學報，2008(6):31 －36.

［7］Ramakrishnan R.Real time estimation of parameters for controlling and monitoring permanent magnet synchronous motors［C］//IEEE International Electric Machines and Drives Conference.2009:1194－1199.

［8］陳中偉，沈艷霞.基于多新息最小二乘的感應電機參數辨識策略［J］.江南大學學報(自然科學版)，2010(5):531 －535.

［9］劉永欽，沈艷霞，紀志成.改進型最小二乘法在PMSM參數辨識中的應用［J］.微特電機，2008(11):19 －22.

［10］丁鋒，謝新民，方崇智.時變系統辨識的多新息方法［J］.自動化學報，1996(1):85－91.

［11］常亮.基于加權多新息方法的系統辨識［D］.哈爾濱:哈爾濱工業大學，2010.

［12］張僑.永磁同步電機參數辨識的研究［D］.武漢:華中科技大學，2010.