基于有限元分析的永磁無刷直流電動機優化設計

黃迪西，崔 群，房 菁

(安徽工程大學，安徽蕪湖241000)

0 引 言

近年來，隨著電力電子技術的發展和永磁材料價格不斷降低，永磁無刷直流電動機得到前所未有的發展。永磁無刷直流電動機可以克服有刷直流電動機換相易產生火花、損耗大、壽命短的缺點;同時永磁無刷直流電動機還具有調速性能好、起動轉矩大等優點［1］。在永磁無刷直流電動機性能分析方法中，國內外應用較多的是基于磁路法的經驗公式或者是基于麥克斯韋方程的電磁場有限元分析。本文利用經驗公式對電機的尺寸和參數進行初步設計，然后利用電磁場有限元分析軟件Ansoft Maxwell V12對永磁無刷直流電動機進行優化設計。

1 有限元分析原理

1.1 二維有限元分析原理

有限元求解的基本原理是將整個區域劃分為許多小的區域，然后將求解邊值問題的原理應用在每個小區域中，最后將各個小區域的結果總和起來得到整個區域的解。在穩態情況下電磁場問題可表示成如下方程組:

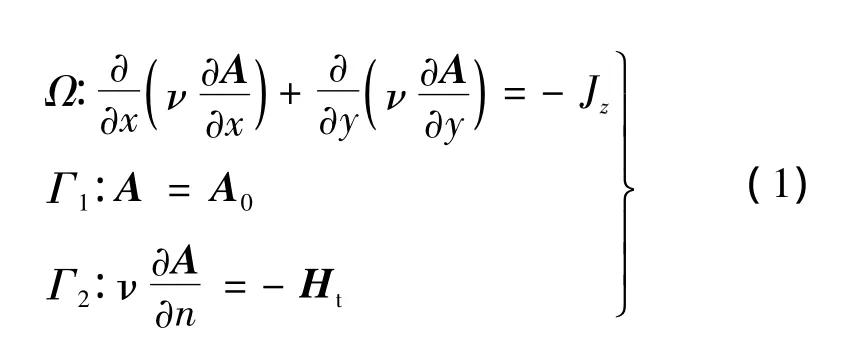
式中:A表示磁矢量;ν表示磁阻率;Ht表示磁場強度的切向分量;Jz表示源電流密度;Γ1表示一類邊界條件;Γ2表示二類邊界條件。

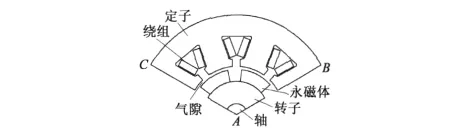
圖1 永磁無刷直流電動機的求解區域

圖1 是無刷直流電動機有限元分析求解域，兩條徑向線上磁場相等，即滿足關系:

電機定子外徑BC處磁場可近似為零，因此需要施加磁通平行邊界條件，即BC滿足關系:

1.2 網格剖分原理

有限元法在電磁場中的應用實質是把麥克斯韋方程組離散化后求解，而求解域的離散化過程的關鍵是對網格進行剖分。通過網格剖分可將式(1)等價于以下變分問題:

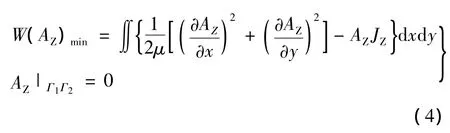
通過利用插值法即可將式(4)條件變分問題轉化為多元函數極值問題，即可得到磁場的數值解。二維磁場中采常用三角形剖分形式，離散網格的劃分決定有限元計算的精度，因此在劃分網格時要確保單元疏密的合理性。圖2是經過剖分離散化后的求解區域。

圖2 永磁無刷直流電動機網格剖分圖

從圖2中可以看出，為保證有限元分析的計算精度，仿真時對電機的特殊求解區域進行了加密處理。

2 二維電磁場有限元分析

2.1 二維有限元模型的建立

根據基于磁路法的經驗公式［4－5］對電機的尺寸進行估算，然后利用Ansoft RMxprt模塊對電機的尺寸和參數進行優化，表1給出了初步經過優化后的電機尺寸。根據表1的尺寸，在Ansoft Maxwell模塊中將電機的二維模型畫出，如圖3所示。

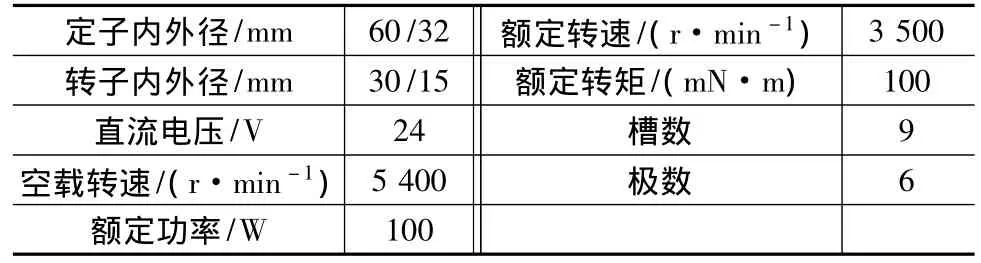
表1 電機主要參數表

圖3 二維模型示意圖

二維瞬態場求解器可以求解模型中存在運動狀態的情況。瞬態場中矢量磁位滿足關系:

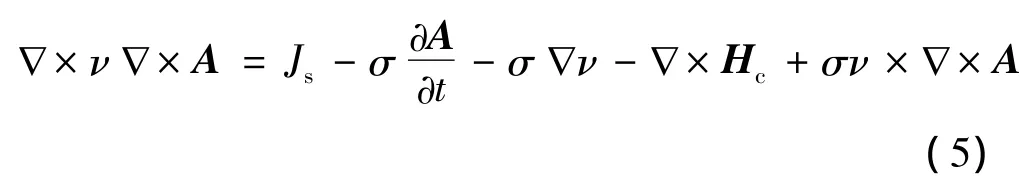
式中:ν表示運動物體速度;Js表示電流密度;Hc表示永磁體矯頑力。

瞬態場求解器中運動方程:

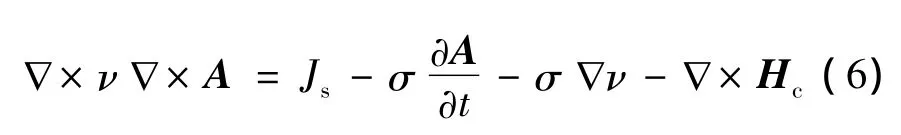
因此，有限元模型中任意時刻的每一點矢量磁位都可獲得。

2.2 考慮電機起動過程的瞬態分析

二維有限元考慮電機的起動過程的瞬態分析，主要考察電機在空載和額定負載的情況下電機轉速能否達到空載轉速和額定轉速以及電機從初始轉速為零到穩速工作狀態的時間信息、電壓電流變化信息等。圖4是電機考慮起動過程時電機性能的曲線。

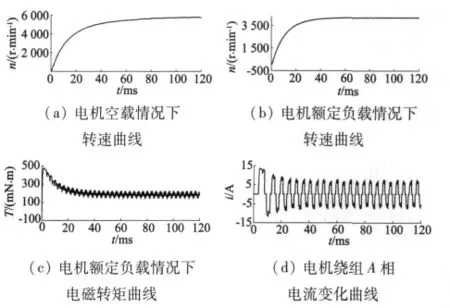
圖4 電機從起動到額定轉速下電機性能曲線

從圖4中可以看出，電機的空載轉速可以達到5 500 r/min，滿足電機設計要求;電機在額定負載情況下，電機轉速最終在4 200 r/min左右平衡，達到了額定轉速為4 000 r/min的要求;電機在穩速下電磁轉矩為190 mN·m，大于電機的額定轉矩;電機在起動過程中電流幅值能達到13 A，明顯高于穩速情況下的電流，由于電機起動時間約為30 ms，持續時間很短，因此起動時的大電流對電機影響不大。

2.3 不考慮電機起動過程的瞬態分析

根據圖4得知，電機在4 200 r/min時穩速，而電機的額定轉速為4 000 r/min，為了分析電機在4 000 r/min時電機的性能，此時不考慮電機的起動過程，將電機轉速固定在4 000 r/min考察電機特性和參數。由于永磁無刷直流電動機的控制器對電機的磁場磁鏈等參數會有影響，因此對電機的仿真分析需要分接控制電路和不接控制電路兩種情況。當不接控制電路時，將電機轉速固定在4 000 r/min，此時電動機相當于發電機空載模式，可以分析電機本體在額定轉速下產生磁鏈、反電勢和齒槽轉矩等信息，為進一步對電機優化提供一定的依據和基礎;當接控制電路時，將電機轉速固定在4 000 r/min，可以分析出電機在額定狀態下，控制電路對電機特性的影響。圖5為不接控制電路時電機特性曲線，圖6是接控制電路的電機特性曲線。

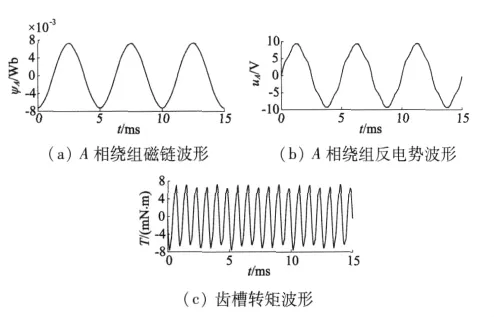
圖5 不接外電路電機在額定轉速下特性曲線

從圖5可以看出，A相繞組磁鏈波形為正弦波，說明氣隙磁場按正弦波分布;反電勢波形近似為正弦波，通過對反電勢波形進行傅里葉分析可得出反電勢的THD為4% ，滿足電機的諧波要求;電機齒槽轉矩幅值為7 mN·m，齒槽轉矩約占電機額定轉矩的7% ，這說明電機的齒槽轉矩較大，需要對其進一步優化設計。

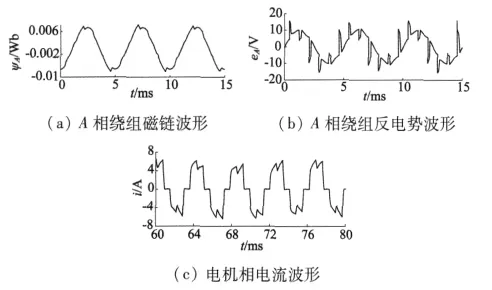
圖6 接控制電路時的電機特性曲線

從圖6可以看出，當電機外接控制電路時，電機的磁鏈和反電勢波形均出現毛刺，這是由于電機控制電路換相時產生的，由于毛刺幅值沒有出現較大波形，且持續時間很短，對永磁無刷直流電動機屬正常現象，若換相毛刺過大，則有可能會出現噪聲，此時需要從電機的齒槽配合和控制器對換相的控制兩個角度來消除噪聲。

3 三維電磁場有限元分析

3.1 電機三維模型及其網格剖分單元的建立

根據永磁無刷直流電動機的二維模型，畫出電機的三維模型，如圖7所示。從圖中可以看出，三維模型考慮了電機的端部效應，即:二維模型只考慮了電機的一個截面，而三維模型考慮了電機的整體。

圖7 三維有限元分析電機模型

三維網格剖分單元類型有很多種，目前應用較多的三維網格剖分單元是四節點四面體網格單元。圖8是一個四節點四面體網格單元在三維坐標中的示意圖。將該網格單元標記為“m”，頂點 i、j、k、l坐標如圖8所示，磁場儲能分別為 φi、φj、φk、φl。對于節點為“i”的形函數 ψmi可表示:

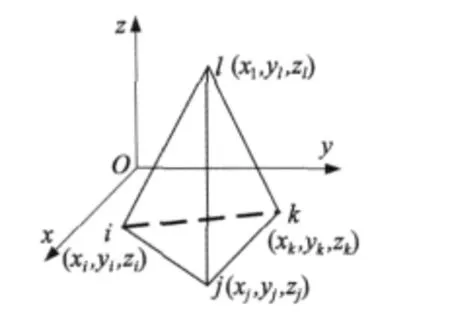
圖8 四面體單元形狀

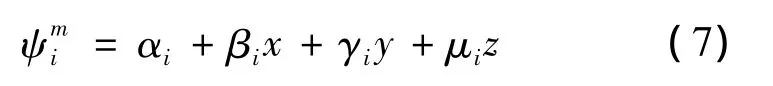
式(8)實際上構成了求解系數的方程組，矩陣形式表示如下:

利用克萊姆法則便可以得到以上4個系數值。矢量磁位函數在該有限元求解域中分布由各個節點的磁場儲能值的乘積疊加而成。

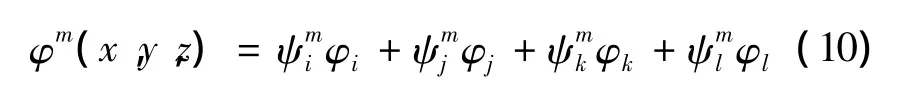
式(10)是關于磁場能量的線性插值函數，能夠求解出每個小的求解域的磁場能量，然后利用累加方法即可求出整個電機求解域的儲能值。圖9是電機模型的網格剖分圖。

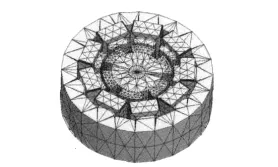
圖9 電機模型的網格剖分圖

3.2 三維靜磁場計算原理及分析

三維靜磁場采用的計算方法是“棱邊法”。三維靜磁場可用來分析永磁材料，對永磁材料的處理通常采用體電流法和等效面電流法。

三維磁場麥克斯韋方程如下:

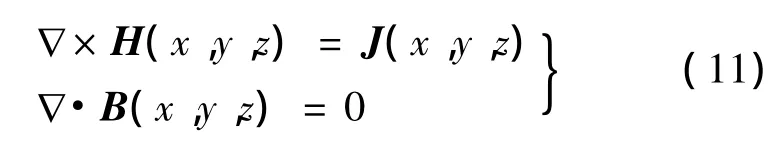
式中:B(x，y，z)為磁感應磁強度;H(x，y，z)為磁場強度;J(x，y，z)為電流密度，這三個矢量的各個方向矢量的函數關系如下:

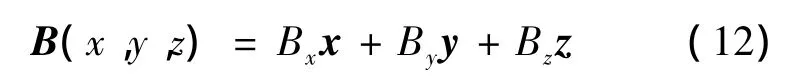
Bx、By、Bz為三個方向上的標量磁感應強度。對于永磁體可按照下式描述:

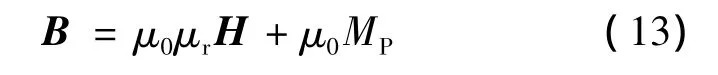
式中:μr為相對磁導率;μ0為真空磁導率;MP永磁材料極化強度。

對于表面貼裝式永磁體，三維磁場將其表示成:

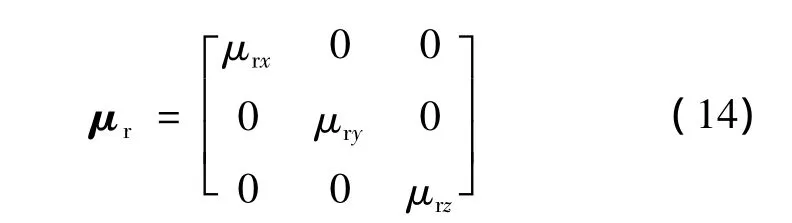
磁場強度H可由下式描述

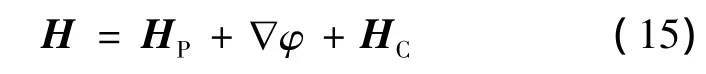
式中:HC為永磁體上的磁場強度;φ為標量磁位;HP為四面體6條棱的磁場強度。

圖10和圖11給出了電機整體的磁密云圖和磁矢量圖。從圖中可以看出，磁密在電機中分布均勻，槽底角處磁密較高，需要將槽底的倒角增大以減小磁密;電機的齒部磁密可達到1.4 T，達到電機最佳齒磁密值，說明電機齒磁密設計合理。圖12是電機氣隙磁場分布。從圖中可以看出，電機氣隙磁密最大值為0.9 T，平均值為0.5 T，均達到電機氣隙磁密的典型值，說明電機氣隙設置合理。

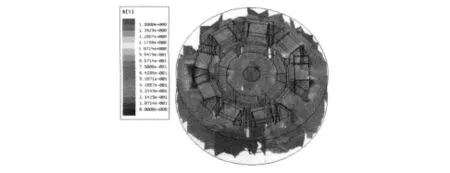
圖10 三維磁場電機磁密云圖

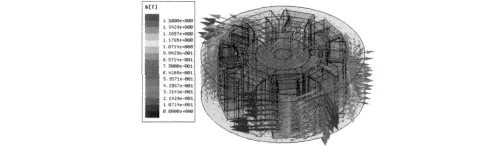
圖11 三維磁場電機磁密矢量分布圖

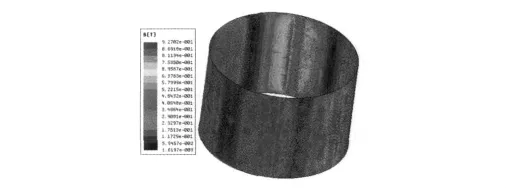
圖12 電機氣隙磁場分布圖

4 實驗結果及討論

本文對額定功率為45 W的永磁無刷直流電動機的樣機進行實驗。24 V直流電源給控制器供電，控制器驅動電機的三相繞組。電機的負載轉矩由轉矩測試儀給定，通過轉矩測試儀可以給電機加上不同的負載。

實驗表明:電機的空載轉速可以達到6 000 r/min，電機的額定轉速可以達到4 000 r/min，均滿足設計要求。圖13是4 000 r/min時相電流波形圖。從圖13波形圖中可以看出，電流導通時段平均值約為6 A，與仿真的結果(圖6(c))相近，實驗的波形與軟件仿真的波形也相同，說明電機的整體性能和參數可滿足要求。

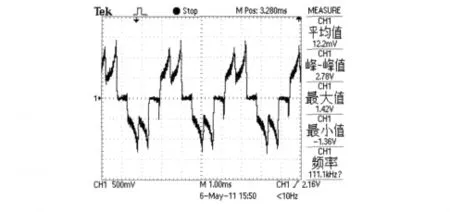
圖13 4 000 r/min時相電流波形圖

5 結 語

本文根據磁路法中永磁無刷直流電動機設計的經驗公式和Ansoft軟件的RMxprt模塊對電機進行設計，建立電機的初始模型，然后利用 Maxwell 2D和3D模塊來對電機初始模型進行優化設計，完成電機整體性能的仿真。在2D模型中通過對電機的瞬態起動過程的分析，在3D模型中通過對電機各部分磁場分布的觀察，從而提出了對永磁無刷直流電動機設計的完整過程及其相應的方法。仿真計算結果和實驗數據表明，有限元分析法可以得到較為準確的計算電機的起動性能、運行狀態等參數，可以實現性能最優的目標。

［1］陳亞玲.永磁無刷直流電機的發展及應用［M］.電氣開關，2010(04):62 －63，66.

［2］Hutton D V.有限元分析基礎［M］.武建華，譯.重慶:重慶大學出版社，2007.

［3］趙博，張洪亮.Ansoft 12在工程電磁場中的應用［M］.北京:中國水利水電出版社，2010.

［4］陳世坤.電機設計［M］.北京:機械工業出版社，2000.

［5］唐任遠.現代永磁電機理論與設計［M］.北京:機械工業出版社，1997.

［6］Yamazaki K.A quasi formulation for analyzing characteristics of induction motors with skewed slots［J］.IEEE Transactions on Magnetics，1998，34(5):3624 －3627.

［7］Valtonen M S M，Parviaiene D S A，Pyrhānen J.Electromagnetic field analysis of 3D structure of axial－flux solid－rotor induction motor［C］//International Symposium on Power Electronics，Electrical Drives，Automation and Motion，Taormina，Italy，2006，39(20):12－16.

［8］王長清.現代計算電磁學基礎［M］.北京:北京大學出版社，2005.