平動式嚙合電機聯合仿真研究

李瑞華

(許昌學院，河南許昌461000)

0 引 言

平動式嚙合電機是一種利用定、轉子間的磁場力驅動轉子帶動內平動嚙合齒輪機構［1－2］輸出低速大扭矩的高集成度電機。目前，平動式嚙合電機已研制出多種樣機［3－7］，并進行了相關的理論研究，研究重點集中在靜態磁場特性、磁路模型、控制方法等方面，這些研究主要有以下問題:一是采用的方法是基于等效磁路模型的解析方法，缺乏精確性和實用性;二是現有的研究都未將內平動嚙合傳動機構與電磁系統進行綜合分析，建立的機械傳動模型較為簡單，不能夠準確地描述平動式嚙合電機的運行特性。產生以上問題的原因是由于平動式嚙合電機的磁場特性與內嚙合機構較為復雜［8］，齒輪嚙合的力學模型、磁場非線性特點使得該電機建模困難，精度也較差，這極大地影響了平動式嚙合電機的發展。

本文提出了一種基于數值軟件仿真分析的平動式嚙合電機模型建立方法。分別采用磁場分析軟件Ansoft Maxwell獲得了電機的磁場力、磁鏈與氣隙之間的特性，利用剛體動力學分析軟件MSC Adams建立嚙合與傳動模型，將磁場分析數據導入控制軟件MATLAB建立磁場力與電流、氣隙的關系模型，并將MSC Adams建立的嚙合與傳動模型導入MATLAB中，建立了平動式嚙合電機的機、電、磁聯合仿真模型，可以較為準確且動態地分析平動式嚙合電機。

1 運行原理與結構

本文以較為新型的雙轉子平動式嚙合電機［9］為分析對象進行研究，其結構原理如圖1所示。該電機的主要特征是在徑向上布置了內轉子與外轉子兩套轉子，兩套轉子之間為定子及繞組。

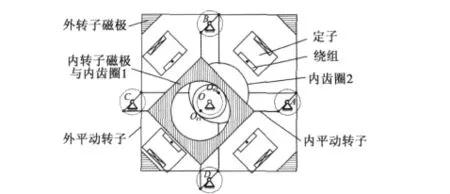
圖1 結構原理

內、外平動轉子上對稱安裝有4個磁極，轉子通過滾動軸承與4個偏心軸連接，偏心軸通過滾動軸承與機殼連接。在偏心軸約束下，內、外平動轉子可以相對于電機中心公轉運動，而不能自轉，同時公轉相位角相差180°，這在徑向上平衡了轉子的偏心慣性力。電機的定、轉子均由硅鋼材料構成，適當控制4個定子繞組的通電順序和電流大小，可以驅動轉子圍繞電機中心O做公轉運動，同時帶動與轉子固聯的內齒圈與外齒輪嚙合，由外齒輪的輸出低速、大扭矩的自轉運動。

根據圖1的原理機構，設計如圖2所示的物理樣機。該電機采用為內齒圈齒數為26，外齒輪齒數為24的2齒差內嚙合機構，傳動比為－13;定子與轉子磁極均采用WTG1500硅鋼片疊制而成。電機整體尺寸94 mm×94 mm×73.5 mm;繞組匝數380匝;定、轉子鐵心疊壓厚度34 mm。

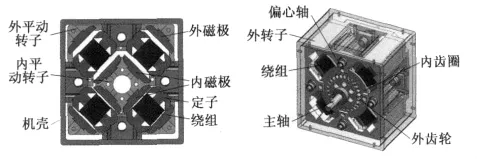
圖2 物理樣機

2 轉矩分析與控制方法

2.1 轉矩分析

從上述的原理機構中可以看出，雙轉子平動電機的轉子只做公轉運動，定、轉子的磁極面在任意公轉位置都相互平行，轉子受到的磁場力總是指向同一個方向，不發生變化。根據雙轉子平動式嚙合電機的結構特點，圖3為轉子處于任意兩個公轉位置時的受力情況。

圖3中的O為電機幾何中心;O1和 O2代表內轉子(或外轉子)公轉軌跡中的兩個不同位置。根據圖1磁極的分布結構，將右上角設為磁極1，逆時針方向依次為磁極2、3、4。F1、F2、F3和 F4代表轉子中心位于O1時磁極1、2、3和4的磁場力矢量;為轉子中心處于 O2時的磁極力矢量。Fm和兩個位置的磁場合力矢量，θm和為相應的相角，θr和為兩個位置的轉子位置角。

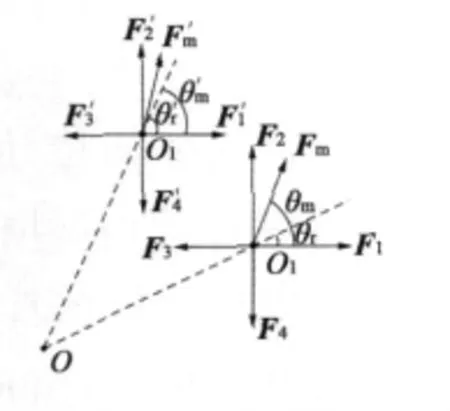
圖3 轉子受力情況

假設轉子處于圖3中的O1位置，Fm的分解為轉子公轉切向力Ft和徑向力Fr，其關系如圖4所示。

由圖4可知，平動式嚙合電機的轉矩依靠磁場合力矢量的切向分力產生，可推導出輸出轉矩表達式:

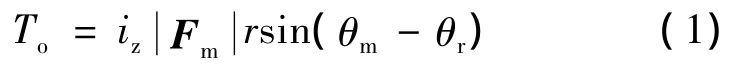
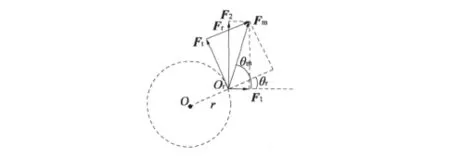
圖4 轉矩形成分析

式中:To為輸出轉矩;iz為減速比;r為轉子公轉半徑，等于齒圈與外齒輪的半徑差。

4個磁極的氣隙長度設為 xa、xb、xc和 xd，它們與θr的關系:

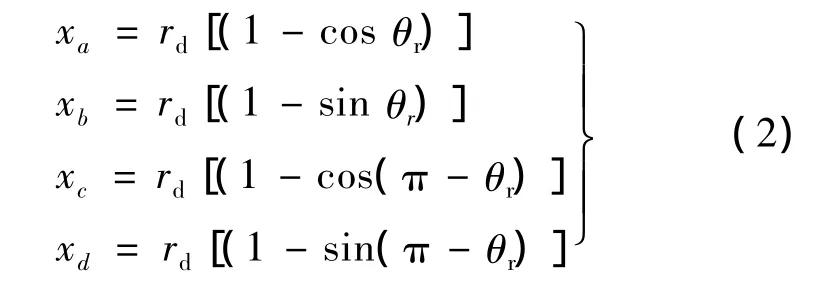
2.2 控制方法

雙轉子平動式嚙合電機的控制方法可以借鑒磁阻電機的控制方法［10－12］。根據式(1)可知，輸出轉矩To與|Fm|和相角θm有關，而Fm是磁極的磁場合力，磁極磁場力是繞組電流和氣隙長度的函數，因此控制磁極磁場力的關鍵是根據不同的轉子位置角，在繞組兩端施加不同的電壓實現電流的調節，從而控制磁場力的大小。

為使輸出轉矩最大，使 θm比 θr超前90°，即 θm－θr=90°，此時 To與|Fm|的幅值成正比。當平動轉子處于不同象限時，參與工作的磁極不同，當平動轉子在圖3所示的第一象限位置時，磁極2、3處于工作狀態;第二象限時，磁極3、4工作;第三象限時，磁極4、1工作;第四象限時，磁極1、2工作。在第一象限時，2、3磁場力可由下式計算:

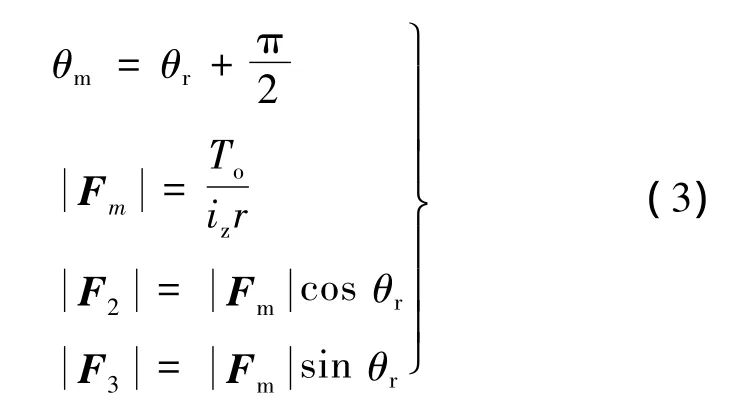
式中:在給定To后，可以計算出磁極磁場力，作為控制目標輸入給控制器調節相應磁極的磁場力。當平動轉子在其他象限時，磁場力計算方法相同，需要考慮的是θr的變換。

3 仿真模型的建立

3.1 嚙合傳動機構仿真模型

MSC Adams提供的MATLAB仿真接口，可將MSC Adams中建立的平動式嚙合電機機械模仿真導入MATLAB中與控制系統聯合仿真。為提高仿真速度，要對電機的嚙合傳動機構進行簡化。根據物理樣機結構，取電機一側的嚙合傳動機構為分析對象，并將機架簡化成和齒圈一體的結構，忽略軸承等附屬配件，簡化后的模型它主要包含兩個齒圈、一個外齒輪、4個偏心軸和一個輸出軸四部分零件構成。圖5為MSC Adams中建立的雙轉子平動電機的機械傳動模型。

圖5 MSC Adams仿真模型

將圖5中的嚙合模型添加約束，并設置狀態變量，利用MSC Adams的Controls插件，導出狀態空間模型，可以導入MATLAB的Simulink環境中。

3.2 磁極模型

磁極繞組的電流i與電壓U、轉子位置角θr有關，使用三維磁場有限元軟件Ansoft Maxwell計算得到其基本形式為ψ(i，θr)的磁化曲線，如圖6所示。

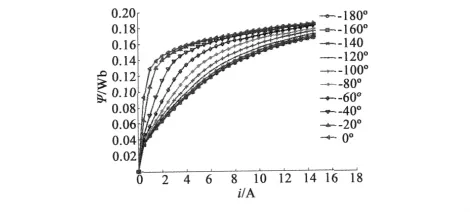
圖6 磁鏈－轉子位置角－電流曲線

為得到i(θr，ψ)形式的磁化曲線，可通過反演的方法［13］，將 ψ(i，θr)轉化為 i(θr，ψ)，如圖7 所示。反演有限元計算結果與Simulink間數據傳遞是整個仿真試驗的關鍵之一。

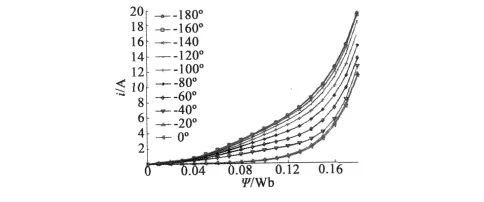
圖7 反演后的i(ψ，θ)

為顯示清楚，圖7中的反演數據只顯示了－180°～0°的10組結果。圖8為有限元計算獲得的磁場力。

圖7、圖8中的數據只計算了 －180°～0°的磁鏈、電流和磁場力特性，在0°～180°時的特性則呈對稱變化趨勢，不必重新計算。忽略驅動控制電路的壓降、鐵心的磁滯和渦流效應，平動式嚙合電機繞組電壓平衡方程:

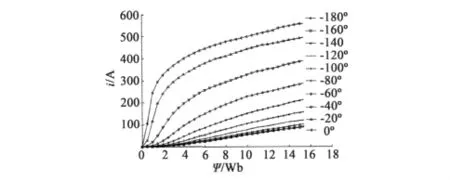
圖8 磁場力有限元計算結果

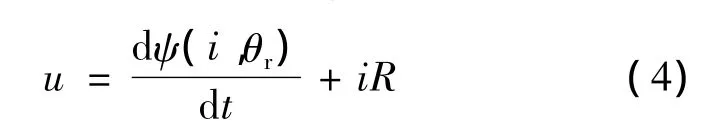
式中:R為繞組電阻。

利用MATLAB中的Lookup_Table模塊可以導入反演的數據，再根據上式可建立磁極仿真模塊如圖9所示。

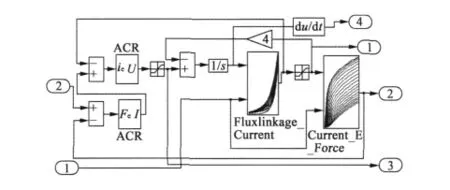
圖9 單相磁極模型

其中的Fluxlinkage_Current為電流查表模塊i(ψ，θ)，里面存儲了反演的數據。依據反演后的i(ψ，θ)曲線簇，任意給定一對(ψ，θ)值，就可以獲得相對應的電流值。Current_E_Force模塊為電磁力查表模塊，在給定電流和轉子位置角后可得到磁極磁場力。AFR為電磁力調節模塊，根據提供的參考電磁力和轉子位置角輸出參考電流;ACR為電流調節模塊，利用PID控制算法對繞組勵磁電流進行控制，輸出參考電壓。

3.3 Simulink聯合仿真模型的建立

在建立了磁極的有限元反演模型后，還需要建立其他輔助模塊，主要包括轉矩－電磁力轉換模塊、磁極位置角轉換模塊。依據平動式嚙合電機的磁場、控制和轉矩特性的特點，在Simulink中構建的RDMM電機整體仿真模型如圖10所示。

圖10中的Torque_Transfer為轉矩－電磁力轉換模塊，根據轉子位置角度和參考電磁力，對應計算出每個磁極需要輸出的參考電磁力，并同時給出邏輯換相關系;RotorAngle_Transfer模塊將轉子位置角轉化為轉子對相對于4個磁極位置的夾角;Pole_A、B、C和D為單相磁極模塊，其內部結構如圖9所示;Fore_TorqueConvert的作用是將4個磁極的電磁力通過式(1)、式(3)計算電機的輸出轉矩;Gear_Model為圖5的機械嚙合傳動機構動力學模型。

4 仿真分析

仿真中設定的參考輸出轉矩為4.8 N·m，負載轉矩為2 N·m，飽和電壓U=60 V，飽和電流18 A。在電機運行的任意時刻，控制模塊中的Torque_Controller模塊根據轉子平動位置角將設定的平動轉矩進行分解，轉換為每個磁極磁場力的參考值，然后輸入給磁極模塊的AFR電磁力調節模塊和ACR電流調節模塊調整磁極磁場力跟隨磁場力參考值。圖11為負載2 N·m時的電機輸出轉速仿真曲線。

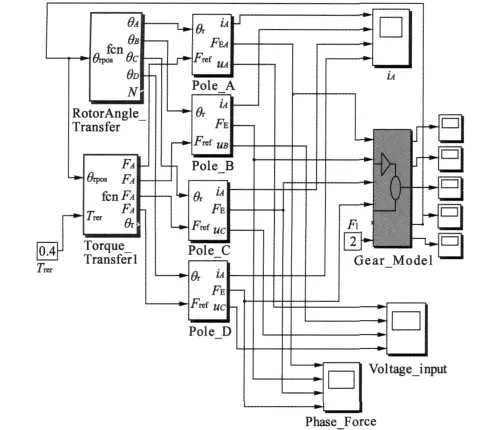
圖10 徑向驅動電機整體仿真模型

圖11中的轉速抖動是由于齒輪嚙合中存在間隙引起的，但是波動較小，變化趨勢說明了電機處于為恒加速狀態。圖12為輸出轉角變化曲線，曲線較為平滑，說明了電機的加速度恒定，輸出轉矩脈動較小。

圖13(a)為磁極2繞組在0.3～0.5 s內的電壓變化曲線，圖13(b)為相應的電流變化曲線，從圖中可以看出，雙轉子平動式嚙合電機的電流也接近正弦波，這與傳統的磁阻電機的電流特性較為相似。

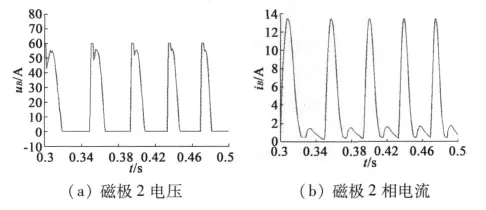
圖13 磁極2電壓、電流變化

為驗證仿真模型的準確性，根據圖2中的結構與參數制作了物理樣機，并進行了加載試驗，物理樣機結構與試驗裝置如圖14所示。

圖14 物理樣機與試驗裝置

圖14 中的實驗裝置由扭矩傳感器和磁粉制動器組成，通過測量軟件能夠實時測量轉角、轉速和轉矩。圖15為物理樣機空載試驗速度曲線與仿真結果的對比，樣機驅動器工作電壓限定在0～60 V范圍內，電流在0～18 A內，與仿真設定一致。

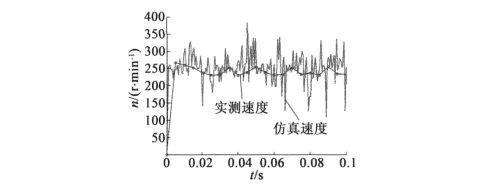
圖15 仿真與試驗結果對比

由于試驗裝置的數據采集系統采樣頻率較低，為200 Hz，而仿真采樣速度較高，造成了圖15中仿真速度曲線波動較大，試驗曲線平直的現象。總體上可以看出，仿真結果與試驗結果較為接近，說明了仿真模型能夠較為準確地描述平動式嚙合電機的運行特性。

5 結 論

平動式嚙合電機的結構較新，沒有可以直接借鑒的磁場分析模型，并且由于其氣隙處于不斷變化中，磁場特性較為復雜，對其定量分析時，磁路方法的計算結果不夠精確。本文利用Ansoft Maxwell、MATLAB和MSC Adams建立了聯合仿真模型對恒轉矩控制算法進行了驗證，仿真結果表明了該模型的準確性，并得到以下結論:

(1)相比于等效磁路方法，有限元方法計算精度高，對于平動式嚙合電機復雜的磁路分析具有較高的可靠性;

(2)使用MSC Adams建立嚙合傳動機構的動力學模型較采用解析方法建立的模型具有簡單直觀和精度高的特點;

(3)利用MATLAB建立的控制模型，容易實現各種控制算法的研究，優化控制方法，提高平動式嚙合電機性能。

［1］崔建昆，周潔深，劉小東.三環減速器的工作原理與功率流分析［J］.機械設計與制造，2005，(2):74 －76.

［2］劉文芝，張乃仁，張春林，等.諧波齒輪傳動中杯形柔輪的有限元計算與分析［J］.機械工程學報，2006:42(4):52－57.

［3］徐強，廖啟征，魏世民，等.新型平動式嚙合電機的運行原理和靜態轉矩［J］.電機與控制學報，2008，12(1):10 －19.

［4］徐強，廖啟征，魏世民，等.平動式嚙合電機的非線性等效磁路模型［J］.電機與控制學報，2008，12(2):126 －131.

［5］徐強，廖啟征，魏世民，等.柔性平動式嚙合電動機結構原理及靜態轉矩［J］.中國機械工程，2009，20(3):288 －292.

［6］李瑞華，廖啟征，魏世民，等.徑向驅動式嚙合電機建模與仿真研究［J］.電機與控制學報，2010，14(4):14 －19.

［7］李瑞華，廖啟征，魏世民，等.徑向驅動式嚙合電機結構設計與靜態轉矩分析［J］.高技術通訊，2011，21(3):297 －302.

［8］趙自強.分流型內平動齒輪傳動特性及其試驗研究［D］.北京理工大學，2009.

［9］李瑞華，丁瑞華，王峰.雙轉子平動式嚙合電動機設計與轉矩分析［J］.機械工程學報，2011，47(23):162 －179.

［10］王勉華，梁媛媛，宋景哲，等.直接轉矩控制在開關磁阻電機中的應用與研究［J］.電機與控制應用，2008，35(2):25 －29.

［11］雷淑英，張慶超，程曉玲.基于轉矩矢量控制的開關磁阻電機汽車驅動系統［J］.天津科技大學學報，2008，23(1):42 －45.

［12］丁文，梁得亮，魚振民，等.基于磁鏈與轉矩特性的開關磁阻電機建模研究［J］.西安交通大學學報，2007，41(2):214－218.

［13］張海軍，高瑞貞，張京軍，等.基于有限元模型的開關磁阻電機系統控制仿真［J］.煤炭學報，2008，7，33(7):831－836.