關于全耦合的一道習題的討論

于歆杰，許 軍，朱桂萍

(1 清華大學電機工程與應用電子技術系，北京 100084)

(2 華北電力大學電氣與電子工程學院，北京 102206)

耦合是“電路原理”課程的重要概念，涉及到耦合的知識點包括互感的定義和性質、耦合系數、互感電壓、同名端(包括定義和測量)、互感的去耦等效、空心變壓器、全耦合變壓器和理想變壓器等概念。

對于自感分別為L1和L2的兩個電感來說，如果它們之間存在全耦合關系，則其耦合系數為1，于是有[1-6]

對于兩個全耦合的線圈來說，如果分別將它們的同名端連接起來，對外則可以構成一個二端網絡，如圖1所示，即為一道習題的電路。

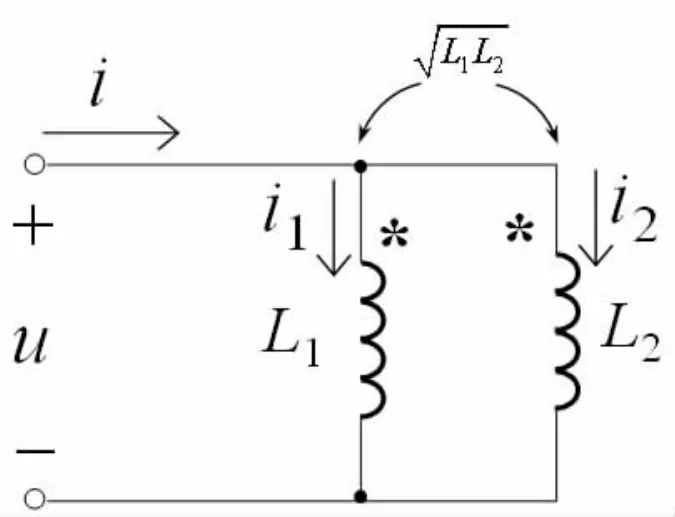
圖1 一道關于全耦合的習題

試證明:當L1≠L2時，該二端網絡對外等效為短路;當L1=L2=L時，該二端網絡對外等效為值為L的電感。

這是一個乍一看起來很特別的習題。證明起來并不太困難，但是怎么理解“除某個特殊情況下該二端網絡對外等效為短路”這個結論卻比較費勁。下面我們從四個角度分別對該題進行分析和討論。

1 從耦合電感的去耦等效出發

如果進行去耦等效，則圖1所示電路可等效變換為圖2所示電路。

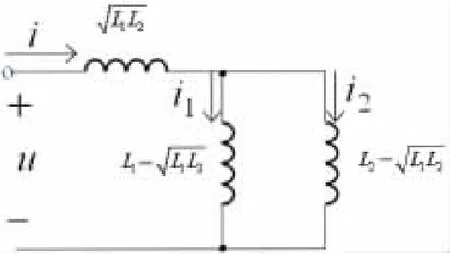
圖2 圖1電路的去耦等效電路

容易看出，這種方法將問題的求解轉化為等效電路中二端網絡入端電感的分析，比較簡潔。本法可訓練學生關于去耦等效和元件串并聯的知識點，但是物理意義并不明顯。

2 全耦合變壓器的伏安關系出發

圖1所示電路相當于將一個全耦合變壓器的原副邊并聯連接起來。在拉氏域中，利用全耦合變壓器的端口關系可知

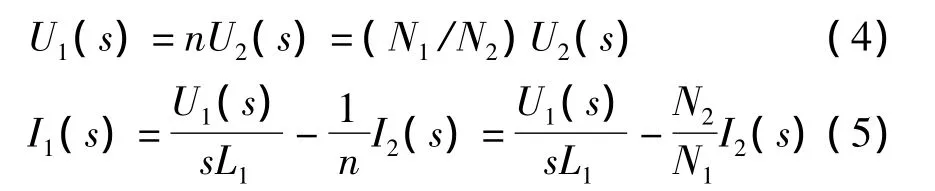
式中，n=N1/N2為變比，N1和N2分別為變壓器原、副邊匝數，I1(s)和I2(s)分別為圖1中i1和i2的象函數，U1(s)和U2(s)分別為圖1中與i1和i2關聯的原副邊電壓的象函數。由于原副邊并聯，因此有

式中，U(s)為圖1中u的象函數。

根據式(4)和式(6)可知，如果N1≠N2(n≠1)，即L1≠L2，則只有當U1(s)=U2(s)=U(s)=0時式(4)和式(6)才能成立。此時對應著端口對外表現為短路，即無電感。

若L1=L2=L，則n=1，式(4)自然滿足。由式(5)和式(6)可得

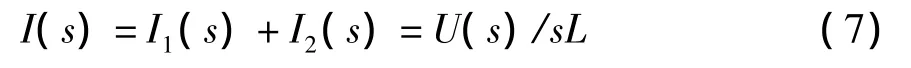
其中，I(s)為圖1中i的象函數。這意味著有

本方法利用全耦合變壓器的端口特性，推導容易，還利用了匝數關系，但物理意義依然不甚明了。

3 從耦合電感等效為流控電源出發

眾所周知，互感電壓可用流控電壓源進行等效。基于這個觀點，可以將圖1所示電路改畫為圖3所示的等效電路(復頻域形式)。

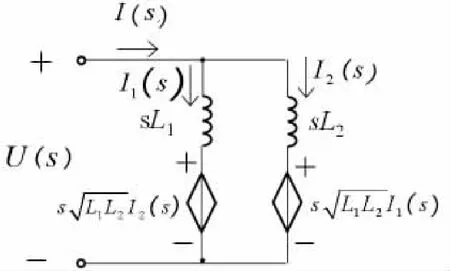
圖3 圖1電路的流控電壓源等效電路

圖3中根據KVL可知

將其代入式(9)可得U(s)=0，即對外表現為短路，無互感效應。

若L1=L2=L，式(9)右側兩部分恒等，即KVL自然滿足。由式(9)可知

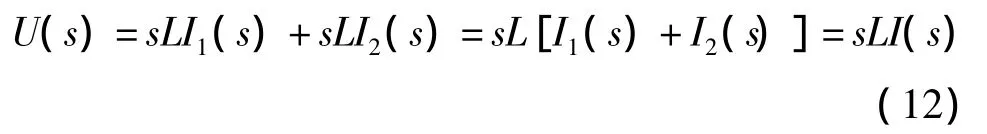
上式表明，對外等效為電感L。

這種方法在分析式(10)的時候可以明確區分L1≠L2和 L1=L2=L兩種情況，而且綜合利用了KCL和KVL，是從電路角度出發比較完整的解法。

4 從磁路和互感的定義出發

如果要想從更基本的角度來考慮這個問題，就需要回到磁路和互感的定義。為了便于分析起見，不妨假設圖1所示的兩個線圈是環形線圈，如圖4所示[1]。圖中實線為原邊線圈，虛線為副邊線圈。容易驗證，二者繞線方式決定的同名端關系滿足圖1要求。

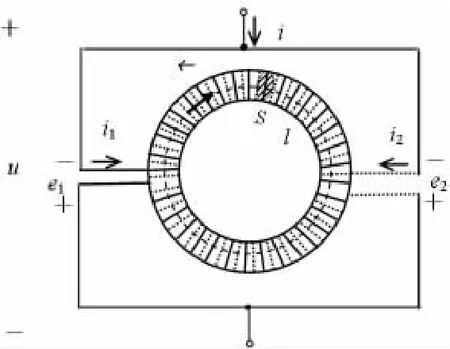
圖4 圖1電路的理想磁路

進一步假設線圈產生的磁場強度在線圈包含的空間中均勻分布，而且不泄漏到線圈以外的空間中(全耦合)，兩個線圈的尺寸完全一樣，磁場通路中均為線性介質，圓環截面積為S，磁路長度為l。則圓環中的磁通為

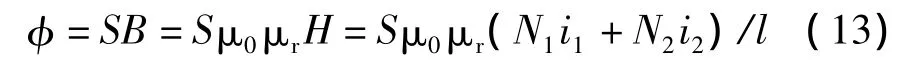
其中，μ0和μr為真空磁導率和介質相對磁導率。

圖4中感應電動勢e1和e2的參考方向是根據電磁感應定律確定的。為突出主要矛盾，在式(13)中設sμ0μr=l。則根據電磁感應定律，有

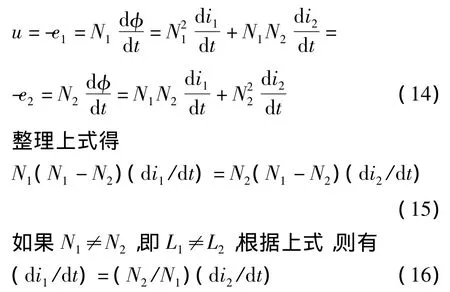
將上式代入式(14)可知u=0，即對外表現為短路，無電感效應。

如果N1=N2，式(14)右側兩個部分恒等，即KVL自然滿足。由式(14)可知

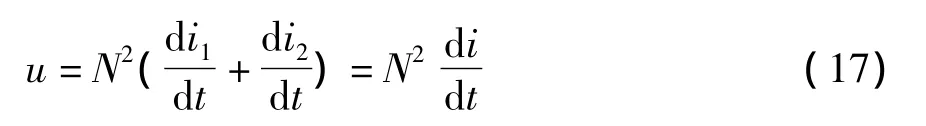
由上式可見，它對外等效為電感L。

雖然第4種方法比較繁難，但對本題能夠提供較好的物理解釋。在條件N1≠N2下，將式(16)與式(13)相結合可知

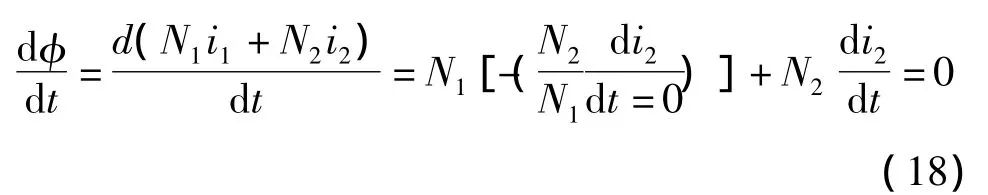
即磁路中磁通變化率為0。這意味著，如果兩個線圈匝數不相等，即使線圈中流過變化的電流。為了確保KVL成立，磁路中磁通變化率也必須為0，自然也就不會產生感應電壓，因此從線圈兩端來看沒有電感效應。關于磁通變化率為0還可以從另一個角度進行解釋:由于穿過每匝線圈的磁通都是相同的，因此磁通變化時在每匝線圈上感應出的電壓也是一樣的。如果線圈匝數不同，則兩個線圈的端電壓會不同。但是端口并聯的邊界條件又迫使兩個線圈端電壓相同，因此必然使得磁通變化率為0。

另一方面，對于條件N1=N2，此時互感的值等于自感。整個網絡可以看作兩個等值電感串聯后再與另外兩個等值串聯的電感并聯，因此對外等效為電感L。或者從另一個角度來理解，該網絡可以看作用兩倍線徑、相同匝數繞制的電感。在理想情況下，其電感值與線徑無關，僅由匝數決定。

下面我們來討論一個看起來更特殊的問題:將兩根導線以相同匝數并聯繞制成一個線圈(這對應著前面討論的N1=N2情況)，將其用于正弦交流穩態下。某個時刻，由于外界情況使得某根導線的繞制情況發生了些許變化(比如發生匝間短路)，這時會發生怎樣的情況?

由于整個二端網絡工作于正弦交流穩態下，因此其中的磁通也是正弦交流穩態變化的。在發生繞制情況變化的瞬間，其磁通具有某個數值。此后，由于兩個線圈的匝數不同，端口電壓相同，迫使磁通一直保持該數值，但變化率為0，對外表現出短路。

這里又揭示出一個可能的應用，即儲能。假設歐姆損耗可忽略，我們可以用兩根導線并繞的方式制成一個線圈，并通以交流電。在適當的時候(比如磁通最大)，人為控制某根線圈的匝數發生改變(比如用開關器件使得某兩匝間發生短路)，則磁場能量就被存儲于該磁路中。在需要使用的時候，可以恢復變化的匝數(比如該開關斷開)，整個二端網絡對外表現為一個電感，可以釋放能量。

相對于直接利用線圈進行儲能來說，該方法不需要用開關切換整個線圈即可完成儲能裝置的投入和切除。或者采用另一種方法，制造兩個不同電感值、全耦合的線圈，先在正弦電路中接入一個電感，磁路中就會產生時變磁通。在某個時刻，投入另外一個電感，此后總磁通將保持在電路切換瞬間的值不變。這種方法比制造兩個電感值完全一致的全耦合電感容易一些。

5 結語

通過前面的討論可以發現，對于本文所示一道習題來說，從四個不同的角度均可求解。各種方法難易程度不同，所能揭示的物理本質也不同。從不同角度求解本題可有助于加深學生和教師對去耦等效、全耦合變壓器、變壓器等效電路、磁路和互感定義的理解。這一點無疑會提高“電路”課程的教學質量。

[1]于歆杰，朱桂萍，陸文娟.電路原理[M].北京:清華大學出版社，2007

[2]周守昌.電路原理(第2版)[M].北京:高等教育出版社，2004

[3]江緝光，劉秀成.電路原理(第2版)[M].北京:清華大學出版社，2007

[4]邱關源，羅先覺.電路(第6版)[M].北京:高等教育出版社，2006

[5]陳洪亮，張峰，田社平.電路基礎[M].北京:高等教育出版社，2007

[6]孫雨耕，電路基礎理論[M].北京:高等教育出版社，2011