無功功率教學新探

田社平，張 峰，陳洪亮

(上海交通大學電子信息與電氣工程學院，上海 200240)

0 引言

正弦穩態電路的功率是正弦穩態“電路理論”或“電路分析”課程教學中的重要內容。在正弦穩態電路的分析中，涉及的功率概念多，包括瞬時功率、平均功率、有功功率、無功功率、表觀功率和復功率等。在教學中，應講清楚各種功率的概念及其相互關系，以及它們的分析與計算方法。筆者在教學過程中，發現作為一組對應的功率概念，有功功率和無功功率在數學定義和物理含義的講授上存在邏輯不一致的地方。對有功功率，其數學定義就是平均功率的定義，即正弦瞬時功率的平均值，其物理含義指電路實際消耗的功率，也即電路中電阻元件消耗的功率。對無功功率，其數學定義則不是來源于某個量(如某個功率量)的平均值，而是基于被分析電路與外電路之間的能量往返交換的現象，將反映能量交換規模的電壓、電流的有效值以及功率因數角的正弦值三者之積定義為無功功率，因此無功功率的大小反映了外電路(電源)參與能量往返的程度[1～3]。

現行教科書上關于無功功率的定義與解釋確有其合理之處，但對于初次學習正弦穩態功率的學生而言，上述問題疑惑頗多。本文試圖提出一種無功功率的教學方法，使無功功率的定義、物理解釋與有功功率保持邏輯上的一致，同時也使無功功率與其它功率概念的聯系變得清晰明確。

1 利用旋轉相量定義無功功率

對于如圖1所示正弦穩態一端口電路，設其端口電壓和端口電流分別為

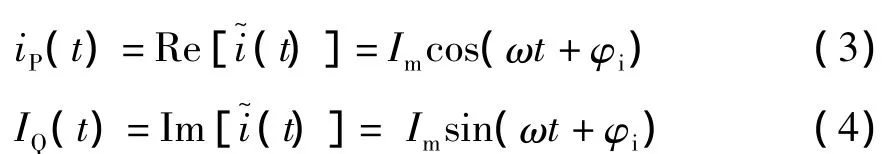
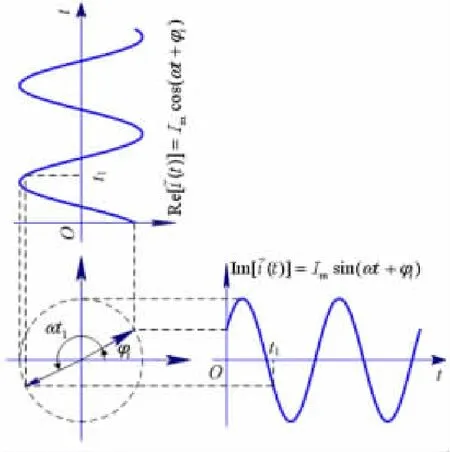
圖2 電流i(t)的旋轉相量在復平面上的投影

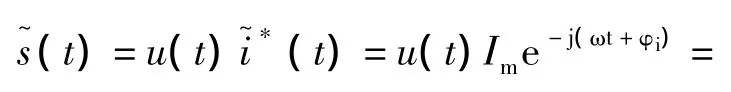
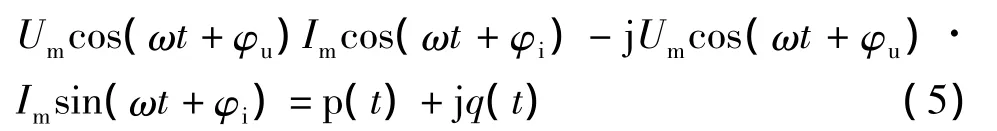
式中，p(t)稱為瞬時有功功率分量，q(t)稱為瞬時無功功率分量。對式(5)兩邊一個周期內(T=2π/ω)取平均值，有

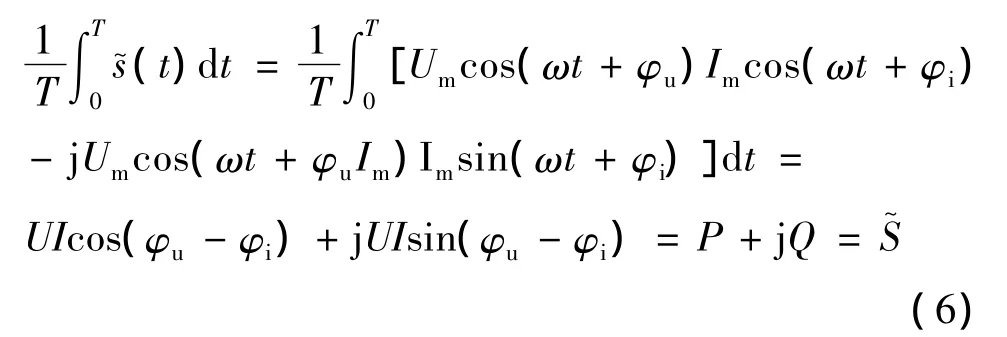
上式是一個非常有趣的結果。我們可以由式(6)來引出無功功率的定義:對圖1所示的電路，定義一個旋轉電流相量，進一步由式(5)定義一個復數瞬時功率，對式(5)在一個周期內取平均值即可定義出有功功率和無功功率這兩個概念。

通過式(6)定義無功功率，不僅使得有功功率和無功功率的數學定義在邏輯上得到統一，即兩者都定義為某一功率量(瞬時有功功率分量或瞬時無功功率分量)的平均值。而且式(6)的物理意義也能得到非常合理的解釋:瞬時電流的有功分量iP(t)是旋轉電流相量在復平面實軸上的投影，它與瞬時電壓(類似地，可以認為其為瞬時電壓的有功分量)相乘得到的功率應看作有功功率的時域表達式;瞬時電流的無功分量iQ(t)是旋轉電流相量在復平面虛軸上的投影，它與瞬時電壓正交，因此它與瞬時電壓相乘得到的功率應看作無功功率的時域表達式。

2 電路元件的無功功率

上面討論了正弦穩態一端口電路的無功功率的定義。在教學實踐中，一般從電路元件吸收功能的情況來引出無功功率的概念。這里討論本文的教學方法在電路元件無功功率教學中的應用。不失一般性，假設元件兩端的電壓為

對于電阻元件則有

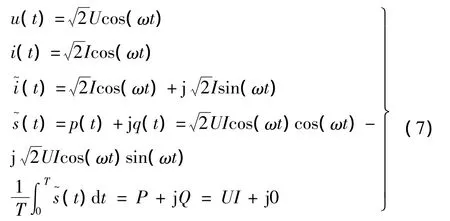
對于電容元件則有

可以看出，采用本文的定義方法，所得到的電路元件無功功率的大小和符號與現行教材完全一致。

3 討論

本文給出了一種基于旋轉相量的無功功率教學方法。該方法于有如下優勢。

(1)無功功率的定義在形式上與有功功率統一。這種統一體現在:①在復平面，在時域，定義了瞬時有功分量和瞬時無功分量兩個對應的功能，它們分別對應瞬時(電流)量在復平面實軸和虛軸上的投影;②無功功率為瞬時無功分量在一個周期內的平均值，與有功功率為瞬時有功分量在一個周期內的平均值相對應;③復數瞬時功率的定義與復功率對應，復功率為復數瞬時功率在一個周期內的平均值。

(2)本文提出的新教學方法與現行無功功率的教學內容沒有沖突。從物理意義而言，有功功率刻畫了耗能元件(電阻)消耗功率的平均值，無功功率則刻畫了儲能元件(電容或電感)吸收功率的平均值;有功功率是消耗掉的功率，而無功功率則是與外電路交換的功率。

(3)現行無功功率的教學內容強調儲能元件與外電路的能量交換，忽視了功率的概念，其根本原因在于沒有將無功功率與某個瞬時功率量(也是一個波動的量)的平均值對應起來。而本文提出的教學方法建立了瞬時無功功率分量的概念，其平均值即為無功功率，這樣可以強調無功功率的“功率”含義。

[1]李瀚蓀.簡明電路分析基礎[M].北京:高等教育出版社.2002

[2]陳希有.電路理論基礎[M].北京:高等教育出版社.2004

[3]于歆杰，朱桂萍，陸文娟.電路原理[M].北京:清華大學出版社.2007