關(guān)于遺傳可遮和遺傳σ-亞緊可數(shù)乘積的注記

趙斌,李秀玲,官春梅

(喀什師范學(xué)院數(shù)學(xué)系,新疆喀什 844007)

關(guān)于遺傳可遮和遺傳σ-亞緊可數(shù)乘積的注記

趙斌,李秀玲,官春梅

(喀什師范學(xué)院數(shù)學(xué)系,新疆喀什 844007)

證明了在逆序列的情形下,可遮空間、強(qiáng)可遮空間在假設(shè)X是可數(shù)仿緊空間的條件下可被其極限空間保持,進(jìn)一步證明了遺傳可遮,遺傳強(qiáng)可遮及遺傳σ-亞緊性在無(wú)需對(duì)投射及極限空間X做任何假設(shè)的情況下即可被其逆極限空間保持.作為上述兩個(gè)結(jié)果的應(yīng)用,分別給出了兩個(gè)相關(guān)的可數(shù)Tychonoff乘積定理.

逆序列；可數(shù)仿緊；可遮；強(qiáng)可遮；遺傳可遮；遺傳σ-亞緊

1 引言及預(yù)備

正規(guī)性及覆蓋性的乘積性質(zhì)的研究是拓?fù)鋵W(xué)中重要的研究方向,通過(guò)逆系統(tǒng)的極限性質(zhì)研究正規(guī)性及覆蓋性的乘積性質(zhì)是一個(gè)有效的方法[1-4].在假設(shè)逆極限空間X是κ-仿緊的通常條件下,注意到關(guān)于可遮及強(qiáng)可遮性逆極限保持問題仍未得到完全解決[5-7].此外,文獻(xiàn)[8-9]利用散射分解,σ-點(diǎn)有限開膨脹分別給出了關(guān)于遺傳可遮及遺傳σ-亞緊的刻劃,并利用這些刻劃研究了遺傳可遮及遺傳σ-亞緊乘積性質(zhì),得到了如下的結(jié)論.

定理A[8-9]設(shè)是遺傳可遮的(遺傳σ-亞緊的),則X也是遺傳可遮的(遺傳σ-亞緊的).

針對(duì)可遮及強(qiáng)可遮性逆極限問題,本文將證明在逆序列的情況下,可遮及強(qiáng)可遮性在通常的可數(shù)仿緊條件下能夠被其逆序列的極限空間所保持.同時(shí)對(duì)遺傳可遮、遺傳強(qiáng)可遮及遺傳σ-亞緊的逆極限性質(zhì)也進(jìn)行了討論,可以看到甚至在無(wú)需對(duì)投射及極限空間X做任何假設(shè)的情況下,遺傳可遮、遺傳強(qiáng)可遮及遺傳σ-亞緊即可為其逆序列的極限空間所保持,作為這一結(jié)果的推論,可直接推導(dǎo)出定理A的結(jié)論.

本文所有的拓?fù)淇臻g簡(jiǎn)稱為空間,除非特別指出所有空間不附加任何分離條件,所有映射均為連續(xù)映射.若X為一拓?fù)淇臻g且A?X,|A|表示集合A的基數(shù).設(shè)A是空間X的子集族且x∈X,記

ω表示自然數(shù)集或最小無(wú)限基數(shù).文中未提及的概念及符號(hào)見文獻(xiàn)[10-11].以下的定義是大家熟知的,重述如下:

定義1.1設(shè)X為空間.

(1)設(shè)κ為無(wú)限基數(shù),稱X為κ-仿緊的,如果對(duì)X的每個(gè)勢(shì)不超過(guò)κ的開覆蓋有局部有限開加細(xì).

特別地,稱X為可數(shù)仿緊的,如果對(duì)X的每一可數(shù)開覆蓋有局部有限開加細(xì).

(2)稱空間X是可遮的(強(qiáng)可遮的),如果X的每個(gè)開覆蓋有σ-互不相交(σ-離散的)的開加細(xì).

(3)稱空間X是遺傳可遮的(遺傳強(qiáng)可遮的),如果X的每一個(gè)子空間是可遮的(強(qiáng)可遮的).

(4)稱空間X是σ-亞緊的,如果X的每個(gè)開覆蓋有σ-點(diǎn)有限的開加細(xì).

(5)稱空間X是遺傳σ-亞緊的,如果X的每一個(gè)子空間是σ-亞緊的.

設(shè)Λ為有向集,稱集族U={Uα|α∈Λ}是定向上升的,如果對(duì)任意的α,β∈Λ且α≤β,有Uα?Uβ.

設(shè)X,Y為拓?fù)淇臻g且f:X→Y為滿射.如果對(duì)滿足f-1(y)?U的任一y∈Y及X中的任一開集U,有y∈int(f(U)),則稱f是偽開映射.

易看出滿開映射及滿閉映射均為偽開映射.

以下引理是證明定理時(shí)需要的.

引理1.1[1]設(shè)X是κ-仿緊空間,Λ為有向集且|Λ|=κ,U={Uα|α∈Λ}為X的開覆蓋且是定向上升的,則存在X的定向上升的開覆蓋V={Vα|α∈Λ}使得對(duì)任意的α∈Λ,有

關(guān)于遺傳性質(zhì),易知

引理1.2(i)空間X是遺傳可遮的當(dāng)且僅當(dāng)X的每一個(gè)開子空間是可遮的；

(ii)空間X是遺傳強(qiáng)可遮的當(dāng)且僅當(dāng)如果X的每一個(gè)開子空間是強(qiáng)可遮的；

(iii)空間X是遺傳σ-亞緊的當(dāng)且僅當(dāng)X的每一個(gè)開子空間是σ-亞緊的.

引理1.3空間X是可遮的當(dāng)且僅當(dāng)對(duì)X的任意開覆蓋U={Uα|α∈Λ},存在σ-互不相交的開覆蓋

證明充分性是顯然的,下證必要性.

若X是可遮的,對(duì)X的任意開覆蓋U={Uα|α∈Λ}(不妨設(shè)Λ是良序的),存在U的σ-互不相交的開加細(xì)W=∪n∈ωWn,對(duì)任意的n∈ω及α∈Λ,令

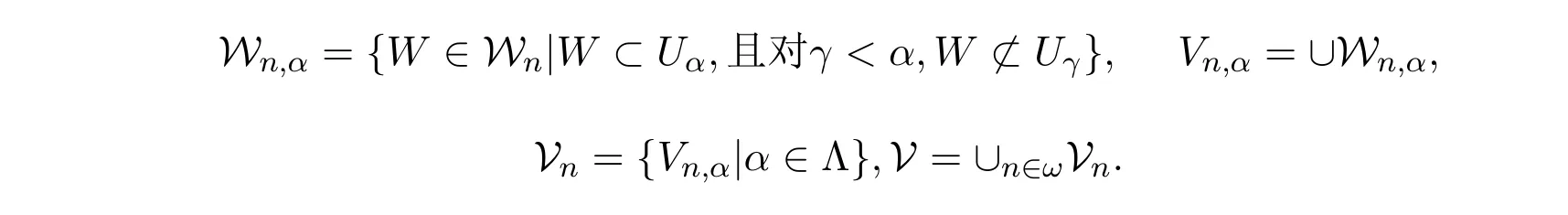
2 可遮,強(qiáng)可遮逆序列的極限及其乘積

在κ-仿緊的通常假設(shè)條件下,可遮、強(qiáng)可遮的逆極限是否可被其極限空間保持這一問題尚未解決[5-7].下面的定理說(shuō)明在逆序列的情形下,假設(shè)極限空間是可數(shù)仿緊空間時(shí),可遮、強(qiáng)可遮性可被其逆序列的極限所保持.

因此,由引理1.5知,X是可遮空間.

仿照文獻(xiàn)[4]定理3的處理方法,利用定理2.1可得到關(guān)于可遮、強(qiáng)可遮性的一個(gè)具有可數(shù)無(wú)限因子的乘積定理.

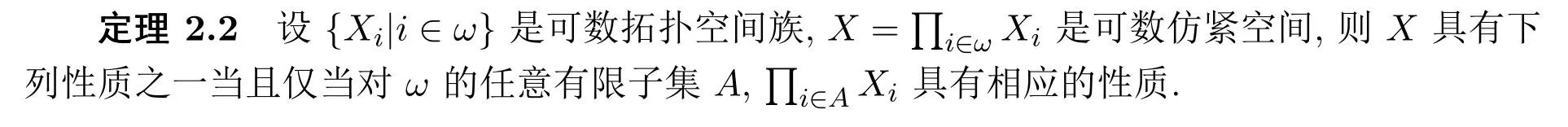
(i)可遮；(ii)強(qiáng)可遮.

3 遺傳可遮,遺傳強(qiáng)可遮,遺傳σ-亞緊逆序列的極限及其乘積

本節(jié)將證明在逆序列的情形下,遺傳可遮、遺傳強(qiáng)可遮性和遺傳σ-亞緊性甚至在不需要對(duì)投射及極限空間X做任何假設(shè)的情況下即可為其逆序列的極限所保持.利用這一結(jié)果可以得到關(guān)于遺傳可遮、遺傳強(qiáng)可遮和遺傳σ-亞緊的一個(gè)關(guān)于具有可數(shù)無(wú)限因子的乘積定理.

定理3.1設(shè)X為逆序列{Xi,,ω}的極限空間.若每一Xi具有下列性質(zhì),則X也具有相應(yīng)的性質(zhì).

(i)遺傳可遮；(ii)遺傳強(qiáng)可遮；(iii)遺傳σ-亞緊.

因此,G是σ-亞緊的,X是遺傳σ-亞緊空間.

類似定理2.2的處理方法,利用定理3.1可以得到下列關(guān)于遺傳可遮,遺傳強(qiáng)可遮,遺傳σ-亞緊的可數(shù)Tychonoff乘積性質(zhì).

(i)遺傳可遮；(ii)遺傳強(qiáng)可遮；(iii)遺傳σ-亞緊.

注意到定理3.2事實(shí)上是文獻(xiàn)[8-9]的主要結(jié)論,是定理3.1的直接推論.

[1]Chiba K.Normality of inverse limits[J].Math.Japonica,1990,35(5):959-970.

[2]Chiba K.Covering properties of inverse limits[J].Question and Answer in General Topology,2002,20:101-114.

[3]Chiba K,Yajima Y.Covering properties of inverse limits II[J].Topology Proceedings,2003,27:79-100.

[4]Zhao Bin.Inverse limits of spaces with the weak B-property[J].Math.J.Okayama Univ.,2008,50:127-134.

[5]熊朝暉.σ-滿正規(guī)空間的逆極限[J].數(shù)學(xué)學(xué)報(bào),2004,47:819-824.

[6]熊朝暉.正規(guī)可遮空間的逆極限[J].數(shù)學(xué)進(jìn)展,1998,27:541-545.

[7]曹金文,賈永進(jìn).正規(guī)強(qiáng)可遮空間的逆極限性質(zhì)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2008,24(1):186-189.

[8]Zhu Peiyong.Hereditarily screenableness and its Tychonoff products[J].Topology and its Applications. 1998,83:231-238.

[9]朱培勇.遺傳σ-亞緊空間及其乘積性質(zhì)[J].數(shù)學(xué)學(xué)報(bào),1998,41(3):531-538.

[10]Engelking R.General Topology,Revised and Completed Edition[M].Berlin:Heldermann Verlag,1989.

[11]Yasui Y.Generalized Paracompactness[M]//Topics in General Topology.New York:Elsevier Science Publishing Company,1989.

Note on countable products of hereditarily screenability and hereditarily σ-metacompactness

Zhao Bin,Li Xiuling,Guan Chunmei

(Department of Mathematics,Kashi Teacher′s College,Kashi844000,China)

In the case of inverse sequence,the screenability and strongly screenability can be preserved by the inverse limit spaces under the usually assumption of countable paracompactness of inverse limit spaces.Furthermore the hereditarily screenability,hereditarily strongly screenability and hereditarily σ-metacompactness can be preserved by the inverse limit spaces even without any assumption of the projections and the inverse limit spaces.As some applications,two theorems about countable Tychonoff product properties are given.

inverse sequence,countable paracompact,screenability,strongly screenability,hereditarily screenability,hereditarily σ-metacompact

O189.11

A

1008-5513(2012)04-0427-06

2012-02-08.

新疆維吾爾自治區(qū)高等學(xué)校科研計(jì)劃重點(diǎn)項(xiàng)目(XJEDU2008I31).

趙斌(1966-),教授,研究方向：一般拓?fù)鋵W(xué)及其應(yīng)用.

2010 MSC:54B10,54D20,54E18