具有退化三次曲線解的Hamilton二次系統的Poincare分支
司成斌
(遼寧師范大學大學數學學院,遼寧大連 116029)
具有退化三次曲線解的Hamilton二次系統的Poincare分支
司成斌
(遼寧師范大學大學數學學院,遼寧大連 116029)
具有退化三次曲線解的Hamilton二次系統,經二次微擾后的Poincare分支,是否存在兩個極限環?這是一個長期受到困擾的問題.本文證明了在特定條件下,可以分支出兩個極限環.
退化三次曲線解;二次Hamilton系統;Poincare分支
1 前言
以往在探討具有代數曲線解的Kolmogorov三次系統是否存在極限環的問題方面,已有許多結果,如文獻[1-2].但對具有代數解的Hamilton二次系統的研究,尚有欠缺.文獻[3]證明了具有非退化三次曲線解的軸對稱三次曲線解的Hamilton二次系統經二次微擾后的Poincare分支不可能分支出兩個極限環.但對于具有退化三次曲線解的Hamilton二次系統的Poincare分支,經二次擾動后是否能分支出兩個極限環,一直沒有結論.本文研究了具有退化三次曲線解的Hamilton二次系統˙x=-y+x2+by2,˙y=x(1-2y),將證明:當b0<b<+∞時,此系統經二次擾動后可以分支出兩個極限環.其中b0是位于區間(77,302)內的一個定點.
考慮具有退化三次曲線解的Hamilton二次系統經二次微擾后的Poincare分支.此系統可統一寫成:
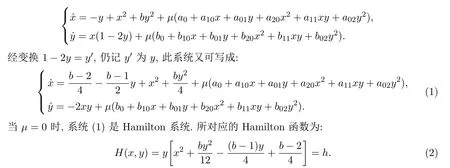
2 曲線族(2)的圖像

時,其圖像為一條閉曲線和一條非閉曲線.如圖1中虛曲線所示.它們分別交y軸于y1,y2,y3.
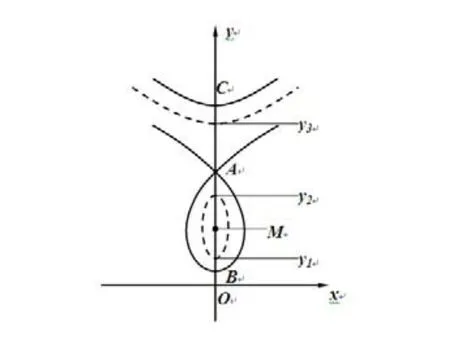
圖1 曲線族(2)當-∞<b<-1時的圖像
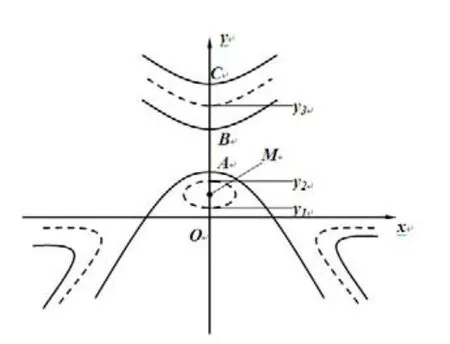
圖2 曲線族(2)當-1<b<0時的圖像


時,(2)式的圖像為一條閉曲線和一條非閉曲線.如圖4中的虛曲線所示.

圖3 曲線族(2),當0<b<2時的圖像

圖4 曲線族(2),當2<b<+∞時的圖像
3 系統(1)的Abel積分
系統(1)的Abel積分為:

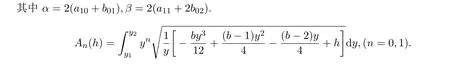
y2和y1分別表示圖1、圖2、圖3、圖4中虛閉曲線的上下確界.A0(h)和A1(h)顯然是線性無關的.所以系統(1)的Poincare分支至少可以分出一個極限環.那么能不能有分支出兩個極限環的可能,關鍵決定于
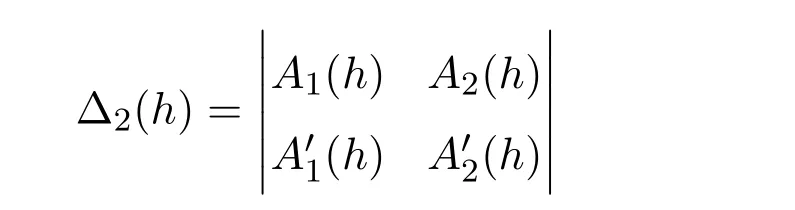
在各自的定義區間內是否存在零點.如果存在零點,則系統(1)就有分支出兩個極限環的可能,如果不存在零點,則系統(1)至多只能分支出一個極限環.其原理可參看文獻[4].
4 Δ2(h)在左端點附近的函數符號
要判定Δ2(h)在定義區間內是否存在零點,可采用分析Δ2(h)在定義區間兩個端點附近的函數符號的方法.如果兩端符號相反,則Δ2(h)在定義區間內必存在零點,否則可驗證Δ2(h)在定義區間內不存在零點.先考慮Δ2(h)左端點,需分-∞<b<0,0<b<3,3<b<+∞三種情形分別進行討論.






5 Δ2(h)在右端點附近的函數符號


為了判斷出φ(b)在-∞<b<-1上的符號,來做φ(b)的函數表:





6 結論
以上第4節和第5節的分析計算的結果可列成表1.

表1 Δ2(h)在定義區間兩端附近的符號
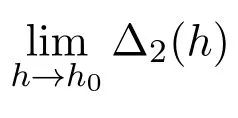
定理系統(1)的Poincare分支,當b0<b<+∞時可以在圖4所示的以同宿軌為邊界的中心環域內分支出兩個極限環.
證明從表1可知在-∞<b<+∞內,只有b0<b<+∞時Δ2(h)在它的定義區間兩端附近的函數符號相反,所以Δ2(h)必存在零點.設此零點為h=ˉh適當地選取系統(1)的參數,可使h=ˉh成為系統(1)的Abel積分A(h)的一個二重零點.根據文獻[5]可知,系統(1)必可分支出兩個極限環,也可分支出一個二重極限環.
至于當-∞<b<-1,-1<b<3和3<b<b0時,從表1看出,這時Δ2(h)在定義區間兩端附近的函數符號相同,其實通過計算機的數值計算,對于每一個給定了b的值,都可以驗證Δ2(h)在它們定義區間內都是定號的,而且也可驗證當b0<b<+∞時Δ2(h)在定義區間內零點是唯一的.類似的驗算方法可參看文獻[6].只是目前尚未找到一般的證明方法,如果這時Δ2(h)確為定號,那么根據文獻[4]可知系統(1)的Poincare分支,當-∞<b<-1,-1<b<3和3<b<b0時能且至多能分支出一個極限環.結合以上定理1就可寫成以下結論:系統(1)的Poincare分支當且僅當b0<b<+∞時,可以分支出兩個極限環,其中的b0是位于區間(77,302)內的一個點.對其它的b,除了臨界情形b=-1,3,b0尚需另行討論之外,至多只能分支出一個極限環.
[1]司成斌,沈伯騫.具有一類三次曲線解的Kolmogorov三次系統的極限環的存在性[J].純粹數學與應用數學, 2004,20(1):84-87.
[2]沈伯騫.具有與兩坐標軸相切拋物線解的Kolmogorov三次系統存在極限環的條件[J].非線性動力學學報, 1996,1(1):85-89.
[3]張芷芬,李承志,鄭志明,等.向量場的分岔理論基礎[M].北京:高等教育出版社,1977.
[4]司成斌,沈伯騫.關于探討Abel積分零點的一個定理[J].數學學報,2007,50(2):443-450.
[5]沈伯騫.具有多重極限環的微分系統的近似系統[J].應用數學學報,1998,21(2):282-287.
[6]Gang Jiatai,Dong Xiangyu,Shen Boqian.Poincare bifurcation for Quadratic systems with a center region of an unbounded triangular Region[J].Ann.of.Diff.Eqs.,2005,21(3):279-285.
The Poincare bifurcation of quadratic Hamilton system with degenerated cubic curve solution
Si Chengbin
(The College of Mathematics Liaoning Normal University,Dalian116029,China)
It is a confusing question whether the Poincare bifurcation of quadratic Hamilton system with degenerated cubic curve solution can be distributed two limit cycles after quadratic disturbance.This paper demonstrates that it can be distributed two limit cycles after quadratic disturbance in specific situation.
degenerated cubic curve solution,quadratic Hamilton system,Poincare bifurcation
O175.12
A
1008-5513(2012)04-0446-16
2011-08-29.
司成斌(1956-),副教授,研究方向:常微分方程定性理論.
2010 MSC:34C05,34C07,34C08

