高頻數據下基于組合預測思想的統計套利策略創新設計與實證研究

楊懷東 潘 珺

一、前 言

市場中性策略是一種通過構建避免某類風險暴露的多空頭寸組合規避市場風險，并利用頭寸間相對價格變化來獲取絕對收益的投資策略。頭寸組合的多頭和空頭需要嚴格匹配，收益水平取決于交易時機與配對組合的選擇能力，而非源于市場走勢。統計套利通過建立時間序列模型擬合資產價格變化規律，識別資產組合內部統計錯誤定價關系，尋找兩個或者兩個以上資產間存在的套利機會，再進一步設定交易閾值，并通過計算機自動發出交易信號執行投資過程，是一種基于統計模型挖掘套利機會的中短期市場中性投資策略。

統計套利策略的技術關鍵在于構建能發現更多、更普遍及更持續套利機會的統計模型以及交易規則的選擇，近期相關研究多集中于此。Bolgun等（2009）對伊斯坦布爾股票交易所ISE30指數成分股日收盤價進行動態統計套利實證結果表明，成對股票組合產生的日平均收益率相對于單純的購買并持有策略高3.36%，但交易限制和交易傭金卻消耗了大部分超額收益率。Low（2009）的實證表明，牛市中股票市場中性策略并不能完全獲得市場收益率，但在熊市中卻能完全避免市場下跌的風險，獲得穩定低風險收益率。Bertram（2009）推導出證券價格服從伊藤擴散過程時基于預期收益率最大化條件下的最優統計套利策略解析式，并運用一只在澳大利亞和新西蘭股票交易所同時上市的銀行股進行了實證檢驗。

國內研究尚處起步階段，研究內容主要集中在局部理論問題與套利策略實證分析。方昊（2005）認為統計套利對象在經濟意義上應具有一定的趨同性，具有相當好的流動性，最后價格比序列也必須是平穩的，并將統計套利模型應用在封閉式基金市場，結果表明統計套利策略是有效的。韓廣哲等（2007）運用方差比分析法將統計套利運用于上證50指數成分股之間的套利，考慮了三種交易成本及費用水平對統計套利策略績效的影響，實證結果表明統計套利策略是有效的，但在樣本外的績效對交易成本相當敏感。常宗琪（2008）基于協整模型并采用日內收盤數據，對鄭州期貨交易所的白糖期貨合約的跨期套利機會進行實證檢驗。研究中將交易進場點為1σ，出場點為2σ，止損點為0.9σ，并進行了簡單演示，并提出可采用日內小時數據來進行統計套利研究。仇中群等（2008）基于協整模型并采用IF0806與IT0807合約的一分鐘高頻數據，對滬深300股指期貨模擬交易進行分析。由交易時機圖發現，價差序列長時間處于無套利帶外，并一直沒有回歸到均值附近，說明股指期貨仿真交易市場存在一定的跨期套利空間，統計套利策略是有效的。徐光梅（2008）同樣采用協整模型對浦發銀行和招商銀行統進行成對交易的實證研究，運用GARCH模型來估計時變標準差，用于交易觸發點的設置，并根據固定交易觸發點與時變交易觸發點將統計套利策略分成兩種策略，實證表明采用時變交易觸發點的策略績效更高。劉華（2008）采用協整模型并基于日數據將統計套利策略中的成對交易運用在上證50ETF與滬深300股指期貨的期現套利上，實證研究表明，統計套利策略在樣本內外均取得了較好的效果，其受市場的影響較小，在各個市場環境中均獲得了比較穩定的收益。

可見，協整模型是國內外統計套利策略的傳統基礎模型，但協整模型估計參數是不變的，而這與金融序列模型參數的時變性是不相符的。張波（2008）將卡爾曼濾波用于投資決策以估計投資收益，文獻則將其運用于估計期貨價格期限結構，均取得了較好的效果。其次，由于市場環境是不斷變化的，模型應用于統計套利策略的效果通常也是時變的。組合預測是綜合各種預測方法以提高整體預測精度的方法，文獻將其運用于預測石油價格、我國的GDP、我國股票市場波動率，均取得了很好的效果，但目前尚無文獻將組合預測思想引入到統計套策略中。此外，采用日數據是傳統統計套利的慣例，但對于高頻數據下的統計套利策略的有效性、配對股票選取及數據頻率對套利績效影響等諸多問題，尚缺少實證分析。

本文選取日數據和5種日內高頻數據，引入估計時變參數的理想模型——卡爾曼濾波模型，并進一步借鑒引入組合預測思想，綜合利用傳統協整模型和新引入的卡爾曼濾波模型，與統計套利策略的具體目標相結合，設計新的組合策略以提高統計套利策略的整體績效，實證分析數據頻率、策略選擇對我國股票市場的統計套利機會及其收益性的影響。

二、基于組合預測思想的統計套利策略創新設計

組合預測是綜合利用各種模型，從而提高整體預測精度。基于這種思想，本文綜合利用協整套利模型及考慮到金融序列參數時變性而引入的卡爾曼濾波模型，結合具體目標對統計套利方案進行設計。

（一）協整模型與卡爾曼濾波模型

（1）協整模型

對價格時間序列協整分析最常用的是恩格爾協整分析兩步法。首先進行OLS回歸分析，運用樣本內數據估計建立的回歸方程：P1t=β×P2t+μt，其中P1t和P2t分別表示兩只具有相關性的股票在t時刻的前復權收盤價，μt為隨機擾動項。然后對回歸方程的殘差序列進行ADF單位根檢驗。

（2）卡爾曼濾波模型

在傳統協整分析中，假定參數β是固定不變的，而金融時間序列模型參數通常是具有時變性的，因此將估計時變參數的理想模型--卡爾曼濾波模型引入到統計套利策略中，用于描述資產價格關系。運用樣本內數據估計建立的量測方程和狀態方程：

量測方程：P1t=βt×P2t+μt

狀態方程：βt=βt-1+θt

其中，μt和θt是兩個相互獨立的隨機誤差項。

（3）價差序列的去中心化處理

采用協整模型和卡爾曼濾波模型得到相應的價差序列Spread，分別求出兩模型下相應的價差長期均值和標準差，然后進行去中心化處理，得到Mspread序列。

（二）基于協整模型及卡爾曼濾波模型的統計套利策略交易信號發出規則

（1）進場點：

當Mspread＞0時，說明回歸方程左邊的股票相對于右邊的股票高估了，而當Mspread大到一定程度時，可以覆蓋雙邊交易成本時，便可以賣出方程左邊的高估股票，買入方程右邊的低估股票，當Mspread回歸到0時便將兩只股票分別平倉獲得利潤。

當Mspread＜0時，說明回歸方程左邊的股票相對于右邊的股票低估了，而當Mspread小到一定程度時，可以覆蓋雙邊交易成本時，便可以買入方程左邊的低估股票，賣出右邊的低估股票，當Mspread回歸到0時便將兩只股票分別平倉獲得利潤。

根據我們的前期研究成果，見文獻，設置較高的交易觸發點是運用高頻數據進行套利時提高收益率的一個有效途徑，因此本文在樣本內外均將采取單次收益率最大化作為進場條件，根據價差的正態分布假設，在95%的置信水平下，價差偏離其長期均值的可能性不會超過1.96倍標準差，因此2σ已是價差偏離其長期均值的最大程度，因此將2σ設置為進場點。由于價差偏離其長期均值的程度處在極限情況下，更有回歸均值的需求，其回復速度也更快，類似于技術分析中的超買超賣現象。

（2）出場點

止損點則采用3σ這個更高的安全界限，同時，為提高收益的實現率，將回復均值的條件放寬為價差偏離長期均值的程度小于或者等于0.5σ。

（三）基于組合預測的統計套利策略規則

（1）進場信號

由于單次收益率最大化策略的進場點設置得比較高，因而交易機會相對較少，基于此，考慮到協整模型和卡爾曼濾波模型效果的時變性，因此只要有一個模型發出進場信號，則進場交易，增加交易機會。

（2）平倉信號

當一段時間內，只有一個模型發出了進場信號和平倉信號，則根據該模型發出的信號進行平倉，以增加收益的實現率。

當一段時間內，協整模型和卡爾曼濾波模型均發出了進場信號和平倉信號，則按較晚發出平倉信號的模型信號進行平倉，以擴大收益率（由于平倉點設置為0.5σ，延長平倉時間，有可能使平倉點更接近均衡點，而使收益率擴大）。

（3）止損信號

當一段時間內，只有一個模型發出了進場信號和止損信號，則根據該模型發出的信號進行止損，防止價差不向均值回歸而造成損失。

當一段時間內，協整模型和卡爾曼濾波模型均發出了進場信號和止損信號，則按較晚發出止損信號的模型信號進行止損，即當兩個模型都已經發出止損信號則進行止損，以避免過早止損而造成收益無法實現。

當t-1日（時刻）止損出場，且t時只有一個模型發出進場信號時，則不進場，避免過早進場造成損失。直至兩個模型都已發出進場信號，則進場交易，以提高進場信號的正確率，從而提高收益的實現率。

三、實證研究

（一）數據來源及處理

數據來源及處理見文獻，統計套利數據選取見表1，并根據該文中我們所取得的前期研究成果，選取同屬煤炭采選業的中國神華與中煤能源作為研究對象。

（二）交易成本及費用說明

機構投資者通常可以享受0.03%的優惠傭金率，單邊單只股票的傭金率為0.03%，印花稅率單邊賣出單只股票0.1%，則完成一次套利所需交易成本為0.32%，再考慮0.1%的流動性成本，則總成本為0.42%。此外，還需考慮融券費用，大多券商的融券費率為9.86%一年，則每天的融券費率為0.027%，按實際使用天數計算。本文研究中，由于運用日數據和60分鐘數據單次套利持續時間較長，因此融券費率按實際天數計算，而運用30分鐘、15分鐘數據進行單次套利的持續時間短，運用5分鐘及1分鐘進行套利則由于同日操作較多而單次套利可能涉及兩只股票的融券，所以這4個頻率的單次統計套利的融券費率簡化計算為0.05%。

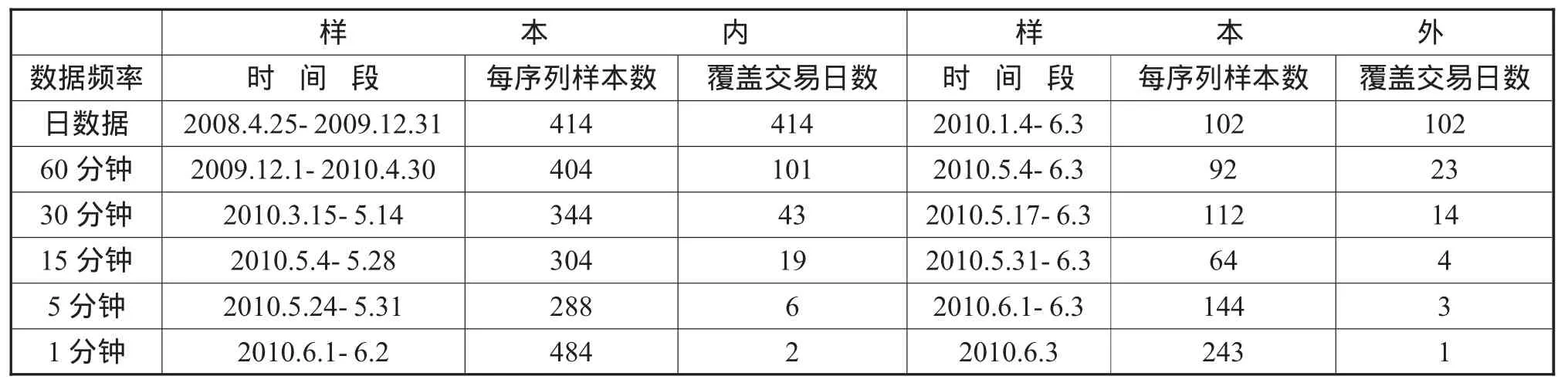
表1 統計套利數據選取

因此，運用日數據和60分鐘數據進行統計的單次成本與費用為0.42%再加實際融券費用，而運用30分鐘、15分鐘、5分鐘及1分鐘數據進行統計套利的單次成本與融券費用和為0.47%。

（三）基于協整模型及卡爾曼濾波模型的統計套

利策略交易信號發出的具體規則

（1）基于協整模型的統計套利策略交易信號發出的具體規則

通過對各頻率樣本內數據進行ADF單位根檢驗發現，12個原價格序列在3個置信水平下均未通過平穩性檢驗，但在1%的置信水平下，12個價格一階差分序列則均通過了檢驗，說明在1%的置信水平下，12個價格序列均為一階單整序列，存在長期協整的可能性。進一步進行協整分析，價差序列的平穩性如下：在1%的置信水平下，5分鐘和1分鐘數據的回歸方程的殘差為平穩，日數據、60分鐘及30分鐘數據的回歸方程的殘差則在5%的置信水平下

為平穩；15分鐘數據的回歸方程殘差在10%的置信水平下為平穩的。可見，中國神華與中煤能源的價格在日數據和5個日內高頻數據上均存在長期的協整關系，均具備統計套利的條件。對6個頻率的價差Spread序列分別去均值進行去中心化處理，日數據、60分鐘、30分鐘、15分鐘、5分鐘及1分鐘數據序列分別為：即 Spread-0.1057、Spread+0.0236、Spread+0.0108、Spread-0.0057、Spread+0.0002、Spread-0.0004分別得到Mspread序列。因此，采用單一協整模型運用日數據和5種日內高頻數據對中國神華和中煤能源進行統計套利的交易信號具體發出規則如表2所示。

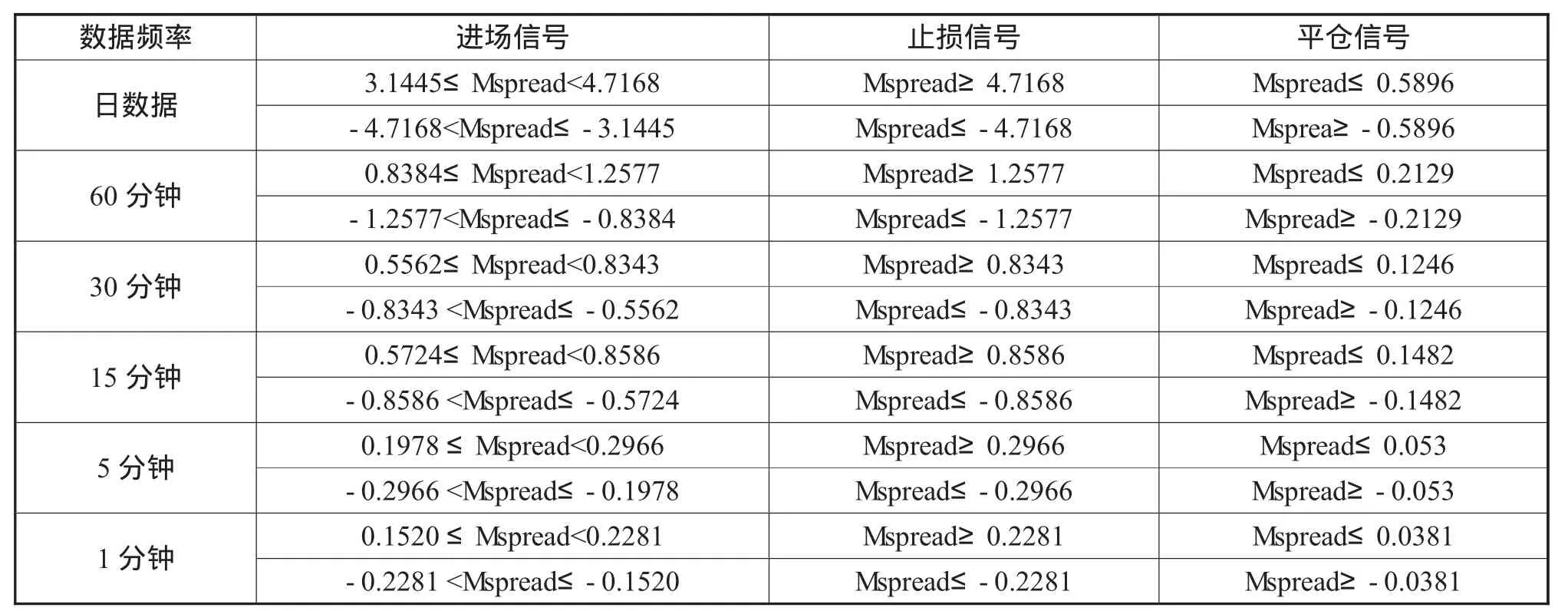
表2 基于協整模型的統計套利策略交易信號發出的具體規則

（2）基于卡爾曼濾波模型的統計套利策略交易信號發出的具體規則

通過協整分析發現，日數據、60、30分、15、5及1分鐘數據的參數β依次為2.454235、2.479564、2.447274、2.430403、2.456503、2.448264，可見 β 參數確實存在時變性，因此將估計時變參數的理想模型——卡爾曼濾波模型引入到統計套利策略中，對β進行估計。卡爾曼濾波的分析結果表明：各個數據頻率的量測方程的擬合程度都相當好，說明卡爾曼濾波分析是十分有效的。進一步計算價差序長期均值和標準差，并對其進行去中心化處理后，采用單一卡爾曼濾波模型運用日數據和5種日內高頻數據對中國神華和中煤能源進行統計套利的交易信號的發出規則如表3所示。

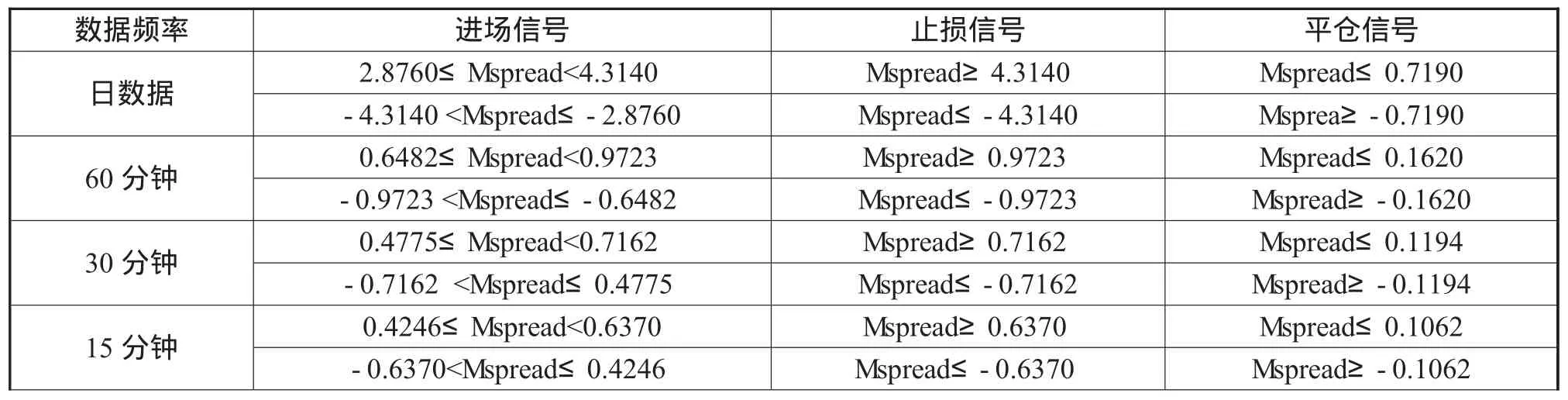
表3 基于卡爾曼濾波模型的統計套利策略交易信號發出的具體規則

-0.2183 ＜Mspread≤-0.1455 Mspread≤-0.2183 Mspread≥-0.0364 5 分鐘 0.1605≤Mspread＜0.2407 Mspread≥0.2407 Mspread≤0.0401-0.2407＜Mspread≤0.1605 Mspread≤-0.2407 Mspread≥-0.0401 1 分鐘 0.1455≤Mspread＜0.2183 Mspread≥0.2183 Mspread≤0.0364

（四）組合策略的績效評估

為了分析組合策略的有效性，將對單獨采用協整模型或者單獨采用卡爾曼模型的統計套利的績效與采用組合策略的統計套利績效進行比較分析。樣本內外采用三種套利方案的績效比較分別如表4、表5所示。

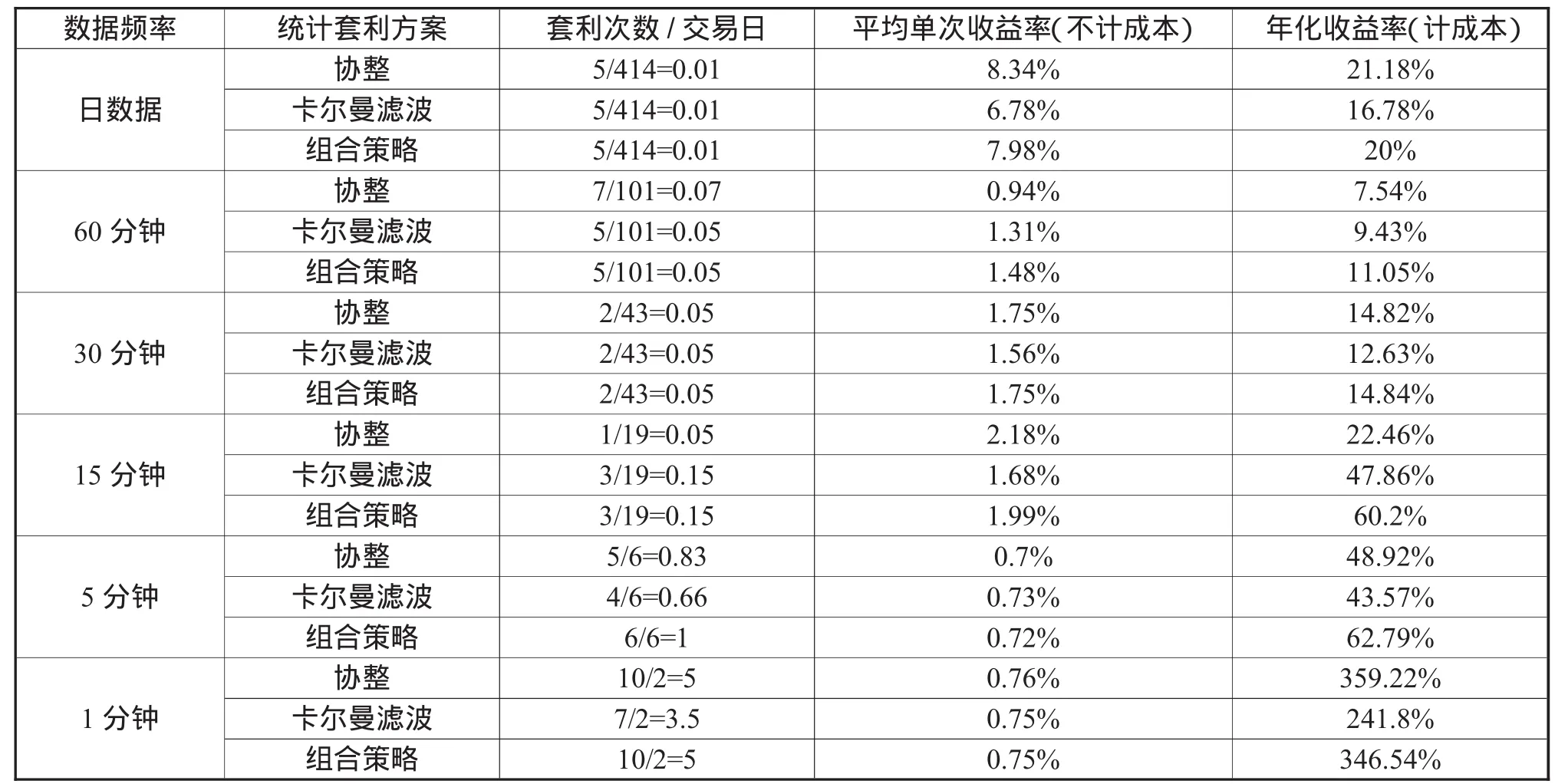
表4 樣本內采用三種統計套利方案進行套利的績效比較

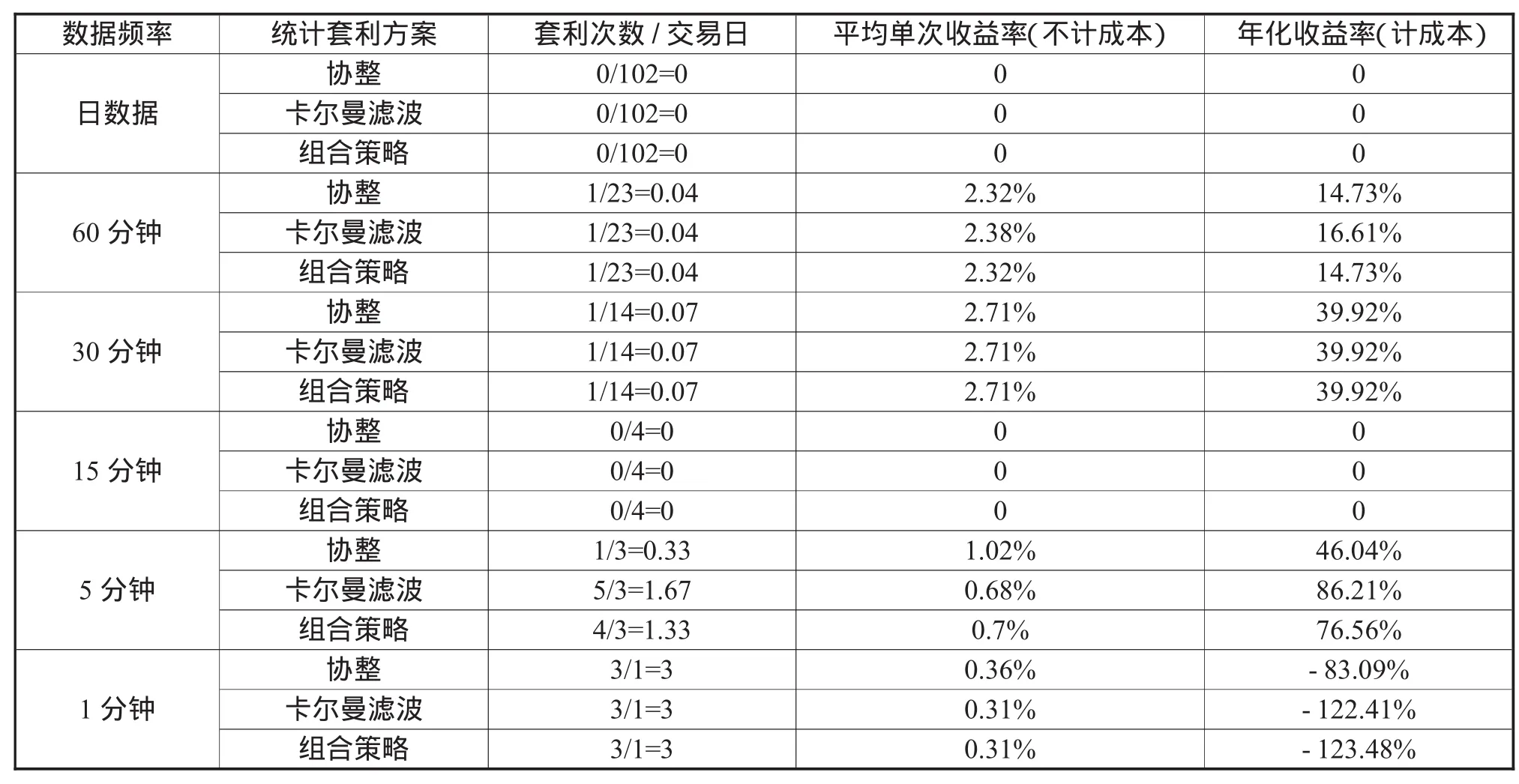
表5 樣本外采用三種統計套利方案進行套利的績效比較

（1）組合策略的必要性分析

從表4可以看出，樣本內，采用卡爾曼濾波模型與協整模型進行套利，各個頻率數據套利的每交易日的交易次數、平均單次收益率均不存在一致變動現象；凈年化收益率方面，采用卡爾曼濾波模型與協整模型運用各頻率數據進行套利時，兩模型效果存在輪流優劣現象。

從表5可知，樣本外，采用協整模型與卡爾曼濾波模型用于統計套利，各頻率數據進行套利時，發出交易信號的次數除了5分鐘數據卡爾曼濾波模型顯著高于協整模型外，其余各頻率的交易信號次數均相同；并且兩個模型在平均單次收益率方面也無明顯優劣之分；在凈年化收益率方面，運用日數據、30分鐘、15分鐘數據時，協整模型與卡爾曼濾波模型效果相同；運用60分鐘及5分鐘數據時，卡爾曼濾波模型優于協整模型；運用 1分鐘數據時，協整模型優于卡爾曼濾波模型。

綜合樣本內外卡爾曼濾波模型與協整模型在統計套利策略中的績效，引入的卡爾曼濾波模型應用于統計套利策略中是有效的，但其與協整模型相比，在各頻率數據上均不存在明顯的優劣之分，由于不同頻率數據對應不同時間段，可見模型效果存在時變性。因此組合策略是必要的。

（2）組合策略的收益性分析

從表4可以看出，樣本內，采用組合策略運用各頻率數據進行統計套利時，在平均每交易日的套利次數方面，基本上大于（15、5分鐘數據）或者接近（日數據、30、1分鐘數據）采用單一模型進行套利時的發出進場信號較多的模型，僅運用60分鐘數據時除外；在平均單次收益率方面，也基本上大于（60分鐘）或者接近（日數據、30、15、5分鐘數據）采用單一模型進行套利時的平均單次收益率較高的模型，僅運用1分鐘數據時除外（由于采用1分鐘進行套利，交易成本影響過大，因此不計）。可見組合策略達到了增加交易機會及擴大單次收益率的目的。在凈年化收益率方面，采用組合策略運用各頻率數據進行統計套利時，全部大于（60、30、15及5分鐘數據）或者接近（日數據和1分鐘數據）采取單一模型進行套利時年化收益率較高的模型，可見其達到了提高整體收益率的目的。因此，樣本內，采用組合策略進行統計套利顯著優于采取單一模型的策略。同時，我們仍要考慮組合策略在樣本外的績效，分析組合策略在樣本外的有效性。

由表5可知，在樣本外，采用組合策略，運用6個頻率數據進行統計套利時，由于日數據和15分鐘數據價差在均值附近波動，沒有出現套利機會，采用60分鐘、30分鐘、5分鐘及1分鐘數據套利時可分別獲得14.73%、39.92%、76.56%及-123.48%的凈年化收益率。并且組合策略下交易信號的準確性得到了很好的體現，由于數據較少，樣本外兩模型的績效僅在5分鐘數據上有顯著區別，此時卡爾曼濾波模型顯著優于協整模型，而組合策略的績效則接近較優的卡爾曼濾波模型績效，可見組合策略能綜合利用兩模型的優勢在5分鐘數據上得到了很好的體現。

（3）組合策略的風險性

由于以上分析均是從收益率方面來考慮的，仍需綜合考慮風險因素，采用最為廣泛使用的夏普比率對該統計套利策略進行評價。夏普比率=（Rp-Rf）/σp其表示投資組合承擔單位風險可獲得的風險收益率與無風險收益率的差值。其值越大，說明收益率對承擔風險的補償程度越高，投資組合績效越好，而其值為負時，則大小排序不具意義。Rp、Rf分別表示套利組合收益率和無風險收益率，其中無風險收益率本文采用一年期定期存款利率2.25%；σp表示套利組合收益率標準差。又因統計套利策略是一個市場中性策略，基于該策略產生的投資組合收益率對市場收益率的敏感程度也是衡量統計策略表現的指標。根據資本資產定價模型（CAPM模型），E（Rp）=Rf+β'[E（Rm-Rf）]，用β'（非前文協整分析中的β）系數表示。本文建立回歸方程Rp=α+β'Rm+ε，運用最小二乘法來計算β'。

采用組合策略構建的套利組合及滬深300指數的夏普比率及β'如表9所示。其中套利組合的夏普比率均考慮了交易成本及費用，而滬深300指數則均未考慮交易成本及費用。

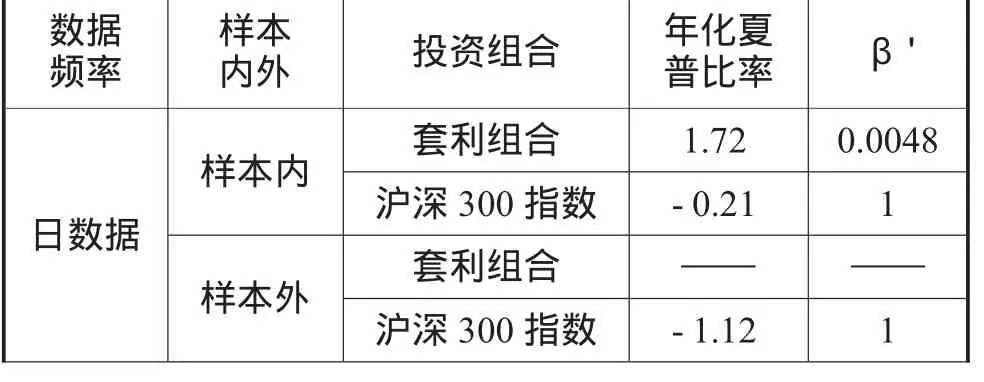
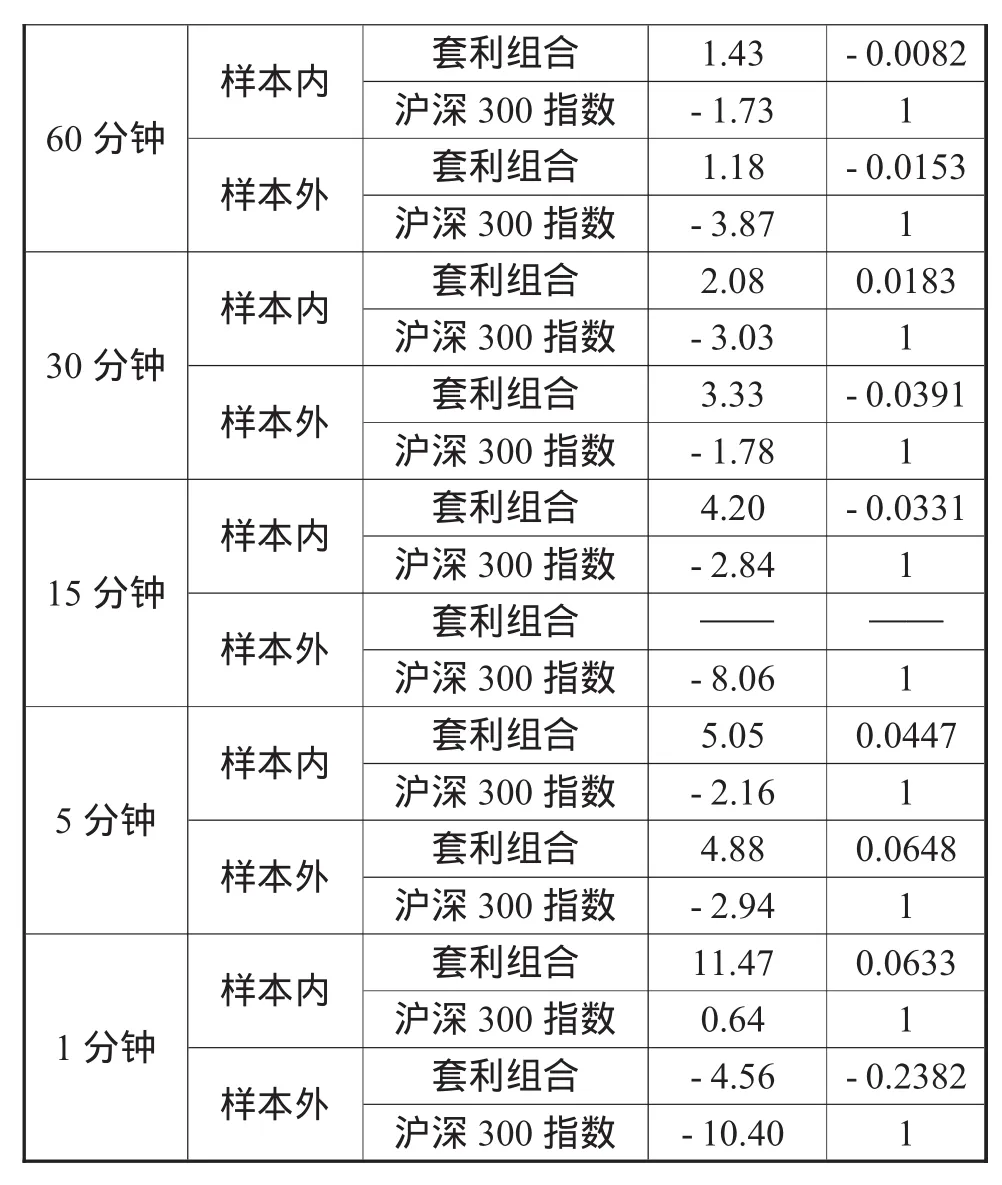
表6 基于組合策略的套利組合及滬深300指數的夏普比率與β'

滬深300指數樣本外 套利組合60分鐘樣本內 套利組合滬深300指數滬深300指數30分鐘樣本內 套利組合滬深300指數樣本外 套利組合樣本外 套利組合-10.40 1.18 1.43-1.73-3.87 2.08-3.03 3.33-4.56-0.0082 1-0.0153 1 0.0183 1-0.0391-0.2382 1滬深300指數 -1.78 1樣本內 套利組合 4.20 -0.0331 5分鐘樣本內 套利組合 5.05 0.0447滬深300指數 -2.16 1樣本外 套利組合 4.88 0.0648滬深300指數 -2.94 1 1分鐘樣本內 套利組合 11.47 0.0633滬深300指數 0.64 1 15分鐘 滬深300指數 -2.84 1樣本外 套利組合 — —滬深300指數 -8.06 1

由表6可知，樣本內，在計成本費用后，組合套利策略在各頻率數據的夏普比率均大于1，說明均有投資價值，采用15、5及1分鐘數據時的夏普比率分別高達4.20、5.05及11.47，可見風險收益率很好地補充了其所承擔的風險，隨著數據頻率提高，年化夏普比率不斷增大；而未計成本費用的滬深300指數在各頻率數據（除1分鐘數據外）的夏普比率均為負，而采用1分鐘數據的夏普比率為0.64，小于1，說明滬深300指數在該研究期間不具投資價值，組合統計套利策略顯著優于指數投資策略。并且套利組合在各頻率數據上的 的絕對值均小于0.01，接近于0，可見組合統計套利策略是市場中性的，能很好地免疫市場風險。

樣本外，計成本費用后，組合套利策略在各頻率數據（除1分鐘數據外）的夏普比率均大于1，說明均有投資價值，采用30分鐘及5分鐘數據時的夏普比率分別高達3.33及4.88，可見風險收益率很好地補充了其所承擔的風險，并且在該策略下運用較高頻率的數據大體上比較低頻率的數據進行套利所獲得的夏普比率較高，而且采用較高頻率數據進行套利時，其套利期限較短，即使和較低頻率獲得的年化收益率相同，其也能分步實現收益率利于資金管理運用，因此較優；而不考慮交易成本及費用時，滬深300指數在各頻率數據的夏普比率均為負，說明滬深300指數在該期間不具投資價值，組合統計套利策略仍然明顯優于指數投資策略。并且套利組合在各頻率數據上（除1分鐘數據外）的 的絕對值均小于0.01，接近于0，可見組合統計套利策略是市場中性的，而采用1分鐘數據的 為-0.24，遠小于1，對市場風險的敏感性很低。

四、結論及展望

本文將組合預測思想引入到統計套利策略中，并利用日數據和五種日內高頻數據進行了實證研究。結果表明：（1）考慮到金融時間序列模型參數的時變性而引入的卡爾曼濾波模型應用于統計套利策略是有效的，但其與傳統協整模型并不存在明顯優劣之分，因此組合策略是必要的。（2）組合策略達到了增加交易機會及擴大單次收益率從而提高整體收益率的目的。樣本內，采用組合策略進行統計套利顯著優于采取單一模型的策略。在樣本外，組合策略交易信號的準確性及綜合利用各模型的優勢也得到了很好的體現，考慮交易成本及費用后，可獲得可觀收益率。（3）綜合考慮風險因素，采用夏普比率及敏感系數對該組合策略進行評價得出，樣本內外，在考慮了交易成本及費用的情況下，組合套利策略在各頻率數據的夏普比率均大于1，說明均有投資價值；且采用高頻數據的夏普比率更高，收益率更穩定。（4）各頻率數據（除樣本外1分鐘數據）的絕對值均小于0.01，近似于0，接近市場中性的，而樣本外采用1分鐘數據的 為-0.24，遠小于1，對市場風險的敏感性很低，可見組合統計套利策略獨立于市場行情，能很好地免疫市場風險。

［1］Bolgun，Evren，Kurun，Engin and Guven，Serhat.Dynamic Pairs Trading Strategy For The Companies Listed In The Istanbul Stock Exchange [J].Working papers，2009

［2］ J Low.Equity Market Neutral：Diversifier Across Market Cycles[J].CREDIT SUISSE ASSET MANAGEMENT，2009

［3］WK Bertram.Optimal trading strategies for It?diffusion processes[J].Physica A，2009（388）：2865～2873

［4］方昊，統計套利的理論模式及應用分析——基于中國封閉式基金市場的檢驗[J].統計與決策，2005：14～16

［5］韓廣哲，陳守東.統計套利模型研究——基于上證50指

［6］常宗琪.白糖統計套利理論模式研究及實例分析[J].經濟師，2008（11）：30～31

［7］仇中群，程希駿.基于協整的股指期貨跨期套利策略模型[J].系統工程，2008，26（12）：26～29

［8］徐光梅.從成對交易到動量檢驗——統計套利的學習與應用：[碩士學位論文].浙江：浙江大學，2008

［9］劉華.基于統計套利ETF期現套利方法應用研究：[碩士學位論文].大連：大連理工大學，2008

［10］張波.不完全信息下基于卡爾曼濾波的投資決策：[碩士學位論文].哈爾濱：哈爾濱工業大學，2008

［11］王蘇生，王麗，陳搏，劉艷.基于卡爾曼濾波的期貨價格期限結構模型[J].運籌與管理，2010，19（1）：113～118

［12］吳虹，尹華.ARIMA與SVM組合模型的石油價格預測[J].計算機仿真，2010，27（5）：264～266

［13］騰格爾，何躍.基于GMDH組合的中國GDP預測模型研究[J].統計與決策，2010（7）：17～19

［14］張偉，廖益琴.基于變權重組合模型的中國股市波動率預測經濟[J].研究導刊，2010（4）：27～28

［15］楊懷東，伍娟.基于高頻數據的成對交易統計套利策略實證研究.第五屆中國管理學年會，2010.11