Markov鏈隨機利率下壽險精算函數的分布模擬

張連增，段白鴿，卜 林

0 引言

當前，隨著計算技術的快速發展和統計軟件的普及，為數值模擬現值隨機變量的概率分布提供了技術支持。一方面，在多數情況下，現值隨機變量的解析計算比較復雜，不如隨機模擬方法直接方便。而且在實務中，對大多數壽險和生命年金產品的評估（如對現值隨機變量的概率分布的研究），可以預期考慮解析解是相當困難的，甚至是不可行的。另一方面，隨機模擬結果也可以作為驗證解析計算的一種途徑。鑒于此，Goovaerts(2000)[1]研究了隨機模擬在現值隨機變量精算函數中的應用。目前，隨機模擬已經成為金融工程與統計研究的常用方法之一，在精算學中必然也將得到廣泛的應用。為此，本文將在Markov鏈隨機利率下，借助于隨機模擬的方法來得到三類有代表性的精算函數的數值解。而Markov鏈作為最基本的隨機過程，已經廣泛應用于工程、經濟科學、社會科學等領域，它具有易于理解、符合直觀、編程方便、自動處理變量的不獨立性問題等優點。另一個值得一提的優點在于，由Markov鏈模擬的隨機利率不會取負值或較大值，這彌補了其它一些隨機利率模型的不足之處。

本文將給出精算學中三個簡單且有代表性的數值實例：20年期年金現值隨機變量與積累值隨機變量、20年期兩全保險的現值隨機變量、20年期期初付生命年金的現值隨機變量，并借助于當前國際上日益流行的R軟件編程實現。解決這些例子的思路與方法可以推廣到精算學與金融學的進一步研究中。

1 理論模型

1.1 Markov鏈

關于Markov鏈的內容幾乎在所有的隨機過程教材中都有介紹，這里只給出最基本的介紹，參見Grinstead和Snell(1997)[2]。考慮離散時間的有限狀態Markov鏈，記為{Xn:n=0,1,2,…}，狀態空間為{s1,s2,…,sn}，轉移概率矩陣可以表示為：

假設矩陣P對應于特征值為1的特征向量是一維的，則該Markov鏈存在唯一的平穩分布。如果記平穩分布為π=(π1,…,πn)，那么它滿足如下方程：

平穩分布的含義可以表述為：如果設X0的概率分布為π，那么對任何n≥1，Xn的概率分布也為π。

另外，在某些條件下，Markov鏈存在極限分布，即當n→∞時，Xn的分布收斂于一個極限，該極限與初始狀態X0無關。而且在很多情況下，極限分布與平穩分布是相同的。

1.2 確定性年金的現值與積累值

考慮期末付年金。對確定性n年期的年金，如果假設在時刻{1,2,…,n}的支付額分別為{b1,b2,…,bn}，在每年內的利率分別為{i1,i2,…,in}[9]，那么該年金在時刻0的現值可以表示為：

為了體現出n個利率{i1,i2,…,in}的影響，在計算年金積累值時，考慮期初付年金。如果假設在時刻{0,1,…,n-1}的支付額分別為{b0,b1,…,bn-1}，那么該年金在時刻n的積累值可以表示為：

1.3 兩全保險

對于(x)歲的n年期兩全保險，在每年內的死亡給付可以不同，而且死亡給付也可以與滿期給付不同。為方便起見，假設死亡給付、滿期給付都是1個單位。對給定的利率軌道{i1,i2,…,in}，該兩全保險的現值隨機變量Z的概率分布可以表示為：

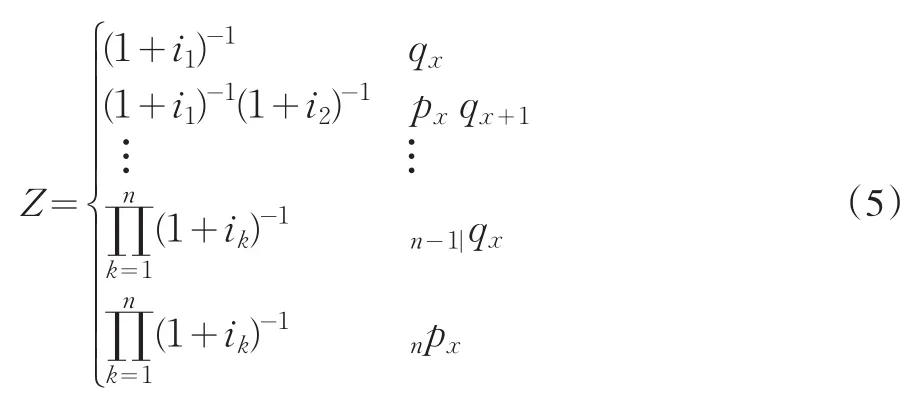
其中，npx、n-1|qx等是壽險精算學中標準的生命表函數（生存概率、死亡概率）。

1.4 定期生命年金

對于(x)歲的n年期期初付生命年金，在每年初的生存給付可以不同。為方便起見，假設給付都是1個單位。對給定的利率軌道{i1,i2,…,in}，該定期生命年金的現值隨機變量Z的概率分布[3]可以表示為：

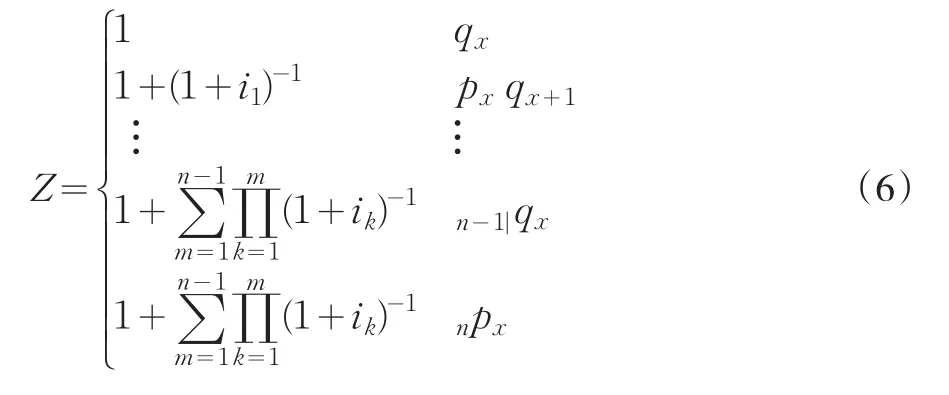
其中，npx、n-1|qx等是壽險精算學中標準的生命表函數（生存概率、死亡概率）。

2 在Markov鏈隨機利率下分布模擬的思路與方法

2.1 產生利率軌道

這里分兩種情況展開討論。第一種情況假設初始利率為常數，第二種情況假設初始利率的概率分布為Markov鏈的平穩分布。在第二種情況下，每個周期內的利率變量是同分布的（但并不獨立）。對每一條利率軌道的產生，都應用Markov鏈的定義。利率軌道條數視兩種不同的情況而定，通常對第一種情況1000條軌道即可，對第二種情況10000條軌道足夠多了。

2.2 確定性年金的現值與積累值

針對每條利率軌道，計算確定性年金的現值[4]與積累值。對所有的利率軌道，重復計算后得到一系列年金現值與積累值的樣本數據，進而通過對這些樣本數據特征的描述便可得到現值隨機變量和積累值隨機變量的概率分布。

2.3 兩全保險

由中國人壽保險業經驗生命表（2000～2003），得到各個年度內的死亡概率，以及保險期限屆滿時的生存概率。針對每條利率軌道，得到一個現值隨機變量的概率分布。對所有的利率軌道，重復計算后得到一系列現值隨機變量的概率分布。這些現值隨機變量的概率分布的特點是：概率值相同，而隨機變量的取值可以不同。

下一步對得到的一系列概率分布進行混合（mixture），最終得到一個完整的概率分布。其原理可以表述如下：

如果設X|Λ=λ的條件概率分布函數為Fλ(x)，而且Λ的概率密度函數為u(λ)，那么X的無條件概率分布函數F(x)可以表示為：

假設模擬的利率軌道共有m條，在對上式進行數值計算時，首先要進行離散化處理。如果設每條利率軌道的權重均為，而且每個Fλ都由離散分布來代替，那么上述積分就可以變為離散求和。具體來說，在本文的兩全保險數值實例中，每一條利率軌道對應一個λ*值，則有，而分布函數Fλ*的形式如式（5）所示。值得注意的是，因為本文數值實例部分采用離散時間的有限狀態Markov鏈，所以不同的利率軌道的現值隨機變量的取值是有可能重復的。

在得到分布函數F(x)之后，即可獲得概率密度函數f(x)，進而可以計算隨機變量X的均值、方差、進一步也可得到各個分位數以及相關的分布度量等。

2.4 定期生命年金

由中國人壽保險業經驗生命表（2000～2003），得到各個年度內的死亡概率，以及生命年金期限屆滿時的生存概率。針對每條利率軌道，便可得到一個現值隨機變量的概率分布[5]。對所有的利率軌道，重復計算后便可得到一系列現值隨機變量的概率分布。最后通過對一系列概率分布進行混合后得到一個完整的概率分布。其計算原理與兩全保險的情形相同，這里不再贅述。

3 數值實例及結果分析

假設Markov鏈利率取值為{0.02,0.03,0.04}，轉移概率矩陣為：

下面通過數值實例進行分析，按照本文第2節的思路，基于Markov鏈隨機利率對三個有代表性的精算函數進行了隨機模擬，得到相應精算函數變量的概率分布及相關的分布特征。這里采用R軟件對其進行算法實現。

3.1 在Markov鏈隨機利率下，模擬確定性年金現值與積累值隨機變量的概率分布

為了簡便，假設年金的支付額都為1個單位。如果利率i為常數，那么這里考慮的期末付年金現值就是通常意義下的其計算公式為：

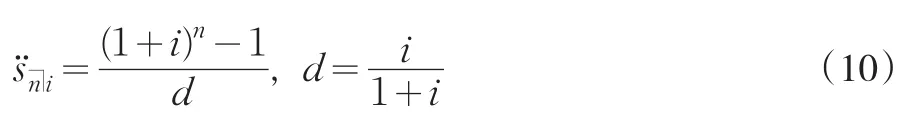
對于20年定期年金來說，根據初始利率的不同假設，下面分兩種情況進行討論。

（1）假設初始利率i1=0.03，每條利率軌道包含20個利率。通過模擬1000條利率軌道，分別得到包括1000個①為了統一，這里采用與本文后續兩個實例相同的處理方式，在年金現值和積累值各自的1000次模擬結果中，不同結果的個數恰好都為1000個。定期年金現值與積累值的樣本數據，進而可以描述該年金現值與積累值隨機變量的概率分布。圖1給出了初始利率為常數0.03情況下，基于Markov鏈隨機利率模擬得到的年金現值與積累值隨機變量的概率分布，其相應的分布特征如表1所示。

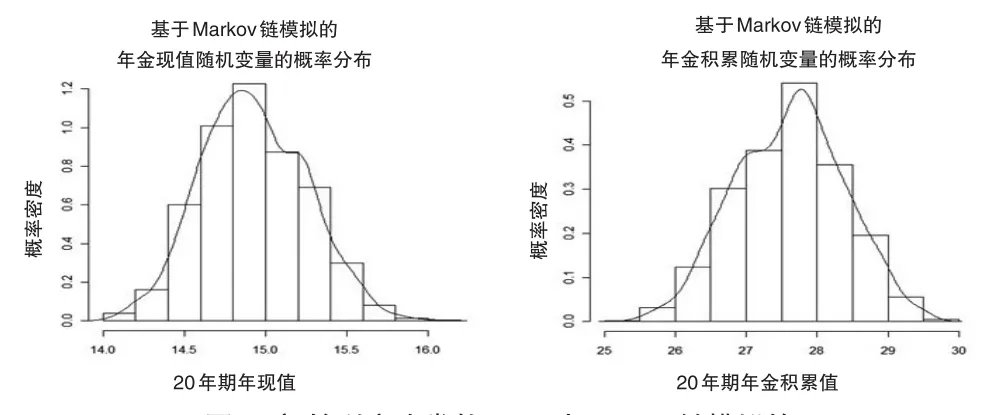
圖1 初始利率為常數0.03時Markov鏈模擬的年金現值與積累值隨機變量的概率分布

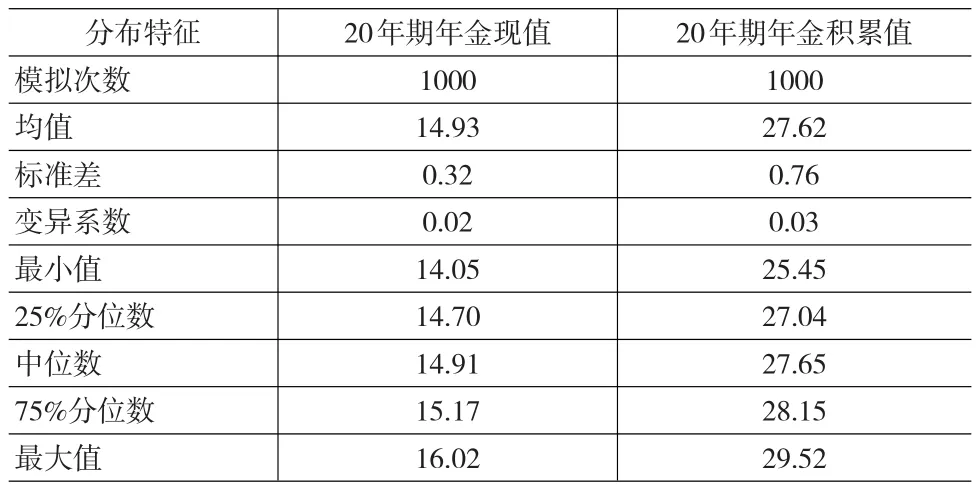
表1 初始利率為常數0.03時年金現值、積累值隨機變量的概率分布的分布特征

為了便于比較，表2給出了利率分別為常數0.02、0.03、0.04情形下，計算的確定性年金現值和積累值。注意到表1中模擬得到的年金現值隨機變量的均值為14.93，積累值隨機變量的均值為27.62，它們明顯處于這三個常數利率計算的現值、積累值的范圍內。這表明在有限的利率波動范圍內，采用確定性利率計算年金現值和積累值是合理的。另外，這兩個均值都與利率為0.03時計算的年金現值和積累值非常接近，這與Markov鏈模擬時初始利率的選擇有關。

若模擬次數為10000次，則得到的年金現值隨機變量的均值為14.93，標準差為0.33；積累值隨機變量的均值為27.57，標準差為0.77。與表1中的均值和標準差相比，差異不大，從一定意義上說，采用1000條利率軌道模擬的結果已相當可靠。

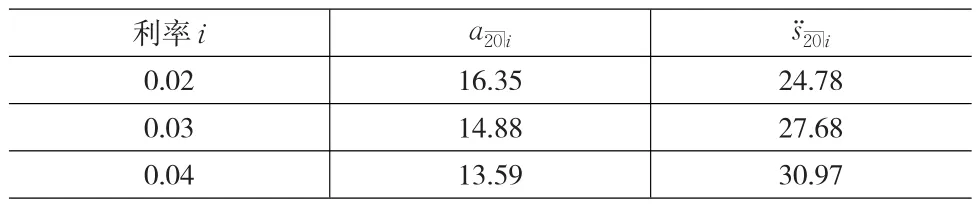
表2 三個常數利率下計算的20年定期年金現值和積累值

（2）假設初始利率的概率分布為Markov鏈的平穩分布，每條利率軌道包含20個利率。經計算，該Markov鏈的平穩分布為 (π1, π2, π3)=(0.2308,0.5769,0.1923)。通過模擬10000條利率軌道，分別得到包括10000個②與注釋①類似，在年金現值和積累值各自的10000次模擬結果中，不同結果的個數都為9991個。定期年金現值與積累值的樣本數據，進而可以描述該年金現值與積累值隨機變量的概率分布。圖2給出了初始利率為平穩分布情況下，基于Markov鏈隨機利率模擬得到的年金現值與積累值隨機變量的概率分布，其相應的分布特征如表3所示。

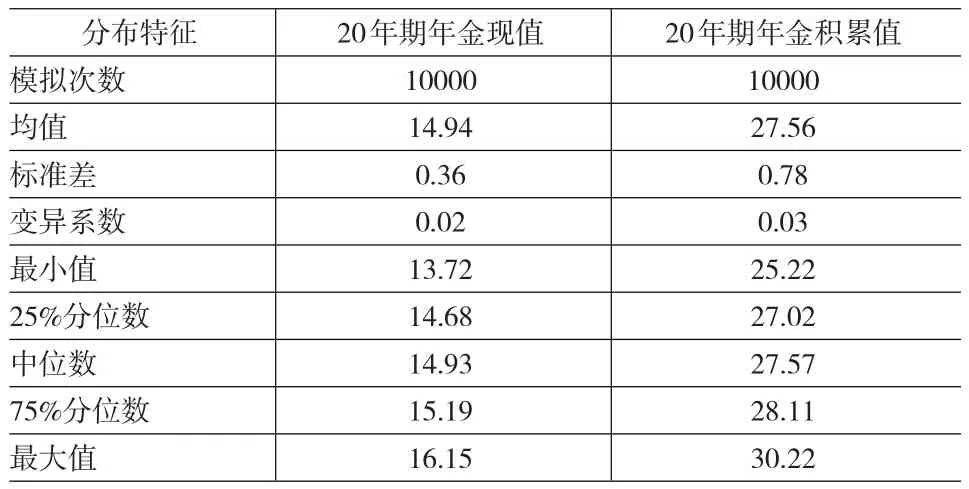
表3 初始利率為平穩分布時年金現值、積累值隨機變量的概率分布的分布特征

注意到表3中模擬得到的年金現值隨機變量的均值為14.94，積累值隨機變量的均值為27.56，它們也明顯處于這三個常數利率計算的現值、積累值的范圍內，且與利率為0.03時計算的年金現值和積累值最為接近。另外，若模擬次數為1000次，則得到的年金現值隨機變量的均值為14.93，標準差為0.37；積累值隨機變量的均值為27.59，標準差為0.77。與表3中的均值和標準差相比，差異也不大，從一定意義上說，這里采用1000條利率軌道進行模擬也是相當可靠的。

3.2 在Markov鏈隨機利率下，模擬兩全保險現值隨機變量的概率分布

考慮關于(30)歲男性的20年期兩全保險，保額為1000元。引用中國人壽保險業經驗生命表非養老金業務表（2000～2003,CL1）。對應于不同的利率假設，其躉繳凈保費及相應的標準差的計算結果如表4所示。

表4 不同的利率假設下兩全保險現值隨機變量的均值和標準差

現模擬計算在Markov鏈隨機利率下，該兩全保險現值隨機變量的概率分布。類似于前面的討論，根據初始利率的不同假設，下面分兩種情況進行討論。

（1）假設初始利率i1=0.03，每條利率軌道包含20個利率。模擬1000條利率軌道，得到1000個概率分布，對這1000個概率分布混合后，得到該兩全保險現值隨機變量的概率分布，如圖3中的左圖所示，其相應的分布特征如表5第二列所示。值得注意的是，這里選定了隨機模擬的“種子”數為set.seed(2525)③應用R軟件進行隨機模擬時，可以設定不同的“種子”數。選擇同一個“種子”數，一方面可以唯一確定模擬結果，另一方面有助于對各種模擬方法的結果進行比較。。在這種情況下，該現值隨機變量的不同取值共有902個。按照從小到大順序排列這些現值，其中第500個現值為655.01，而取值大于655.01的概率僅為1.93%。

（2）假設初始利率的概率分布為Markov鏈的平穩分布，每條利率軌道包含20個利率。模擬10000條利率軌道，得到10000個概率分布，對這10000個概率分布混合后，得到該兩全保險現值隨機變量的概率分布，如圖3中的右圖所示，其相應的分布特征如表5第三列所示。在選定了隨機模擬的“種子”數（set.seed(2525)）后，該現值隨機變量的不同取值共有1240個。按照從小到大順序排列這些現值，其中第700個現值為660.73，而取值大于660.73的概率僅為2.18%。的

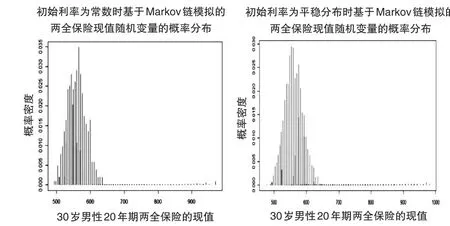
圖3 兩種情況下兩全保險現值隨機變量的概率分布

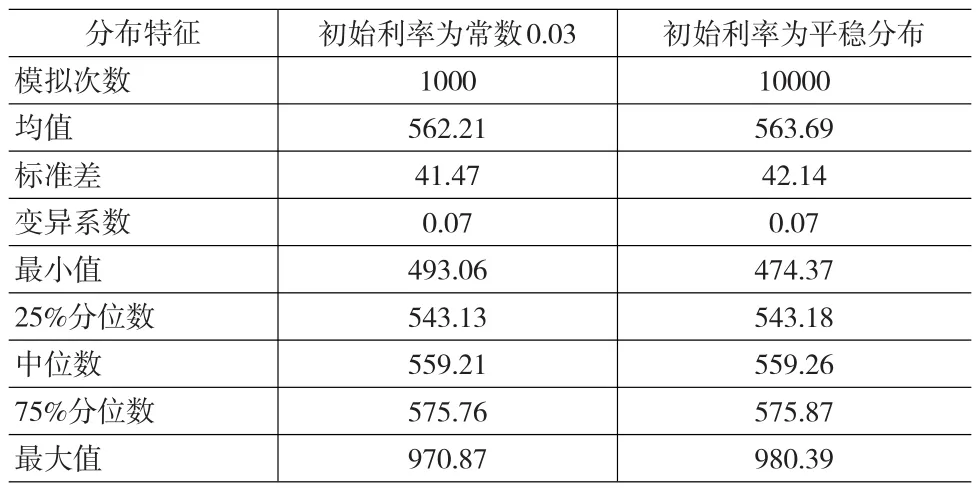
表5 兩種情況下兩全保險現值隨機變量的概率分布的分布特征

與表4相比，兩種情況下模擬得到的兩全保險現值隨機變量的概率分布的均值都明顯處于這三個常數利率計算的躉繳凈保費的范圍內，且與利率為0.03時的躉繳凈保費最為接近。而兩種情況下模擬得到的概率分布的標準差都高于這三個常數利率計算的標準差，這可以直觀地理解為Markov鏈隨機利率帶來了更大的波動性。另外，當初始利率為常數0.03時，若模擬次數為10000次，則得到的兩全保險現值隨機變量的均值為563.29，標準差為41.67；當初始利率為平穩分布時，若模擬次數為1000次，則得到的兩全保險現值隨機變量的均值為562.21，標準差為42.43。從一定意義上說，采用1000條利率軌道對兩種情況進行模擬都是可行的。

從圖3可以看出，兩種情況得到的兩全保險現值隨機變量的概率取值忽大忽小，其概率分布存在多個峰值，并非傳統意義上的單峰分布。當然，從理論上講，這種分布也是存在的，我們可以將其看作是一類特殊的奇異分布。

3.3 在Markov鏈隨機利率下，模擬定期生命年金現值隨機變量的概率分布

考慮關于(30)歲男性的20年期期初付生命年金，為了簡便，假設每次支付額都為1個單位。引用中國人壽保險業經驗生命表非養老金業務表（2000～2003,CL1）。如果利率i為常數，那么這里考慮的精算現值就是通常意義下的其計算公式為：

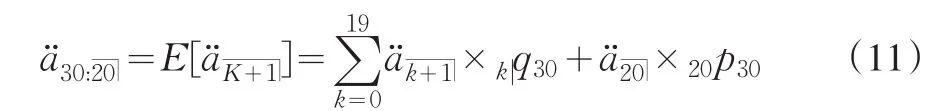
其中，式（11）中的k表示整數生存年數。

對應于不同的利率假設，該定期生命年金的精算現值及相應的標準差的計算結果如表6所示。

表6 不同利率假設下定期生命年金現值隨機變量的均值和標準差

現模擬計算該定期生命年金現值隨機變量的概率分布。類似于前面的討論，根據初始利率的不同假設，下面分兩種情況進行討論。

（1）假設初始利率i1=0.03，每條利率軌道包含20個利率。模擬1000條利率軌道，得到1000個概率分布，對這1000個概率分布混合后，得到該定期生命年金現值隨機變量的概率分布，如圖4中的左圖所示，其相應的分布特征如表7第二列所示。在選定了隨機模擬的“種子”數（set.seed(2525)）后，該現值隨機變量的不同取值共有10846個。按照從小到大順序排列這些現值，其中第5000個現值為12.10，而取值小于12.10的概率僅為1.96%。實際上，經過細致的研究發現，在第5000個現值以后有1000個不同的現值對應的概率都相等，加總后的概率為0.9679，對應的現值隨機變量的取值范圍為[14.56,16.38]。為了更清晰地展示這一特征，圖4中的右圖給出了這1000個不同現值對應的概率值。

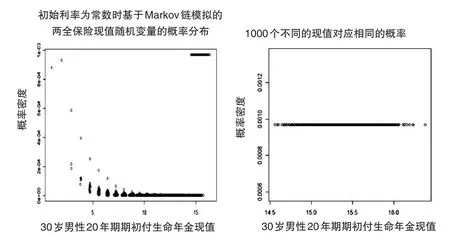
圖4 初始利率為常數0.03時Markov鏈模擬的定期生命年金現值隨機變量的概率分布

（2）假設初始利率的概率分布為Markov鏈的平穩分布，每條利率軌道包含20個利率。模擬1000條利率軌道，得到1000個概率分布，對這1000個概率分布混合后，得到該定期生命年金現值隨機變量的概率分布，如圖5中的左圖所示，其相應的分布特征如表7第三列所示。在選定了隨機模擬的“種子”數（set.seed(2525)）后，該現值的不同取值共有11849個。按照從小到大順序排列這些現值，其中第6000個現值為12.07，而取值小于12.07的概率僅為1.97%。實際上，經過細致的研究發現，在第6000個現值以后也有1000個不同的現值對應的概率都相等，加總后的概率為0.9679，對應的現值隨機變量的取值范圍為[14.42,16.49]。為了更清晰地展示這一特征，圖5中的右圖給出了這1000個不同現值對應的概率值。

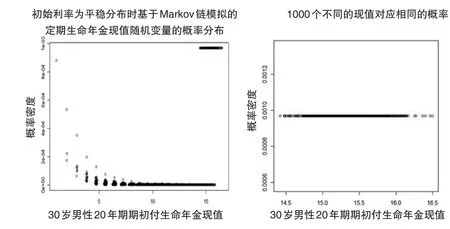
圖5 初始利率為平穩分布時Markov鏈模擬的定期生命年金現值隨機變量的概率分布

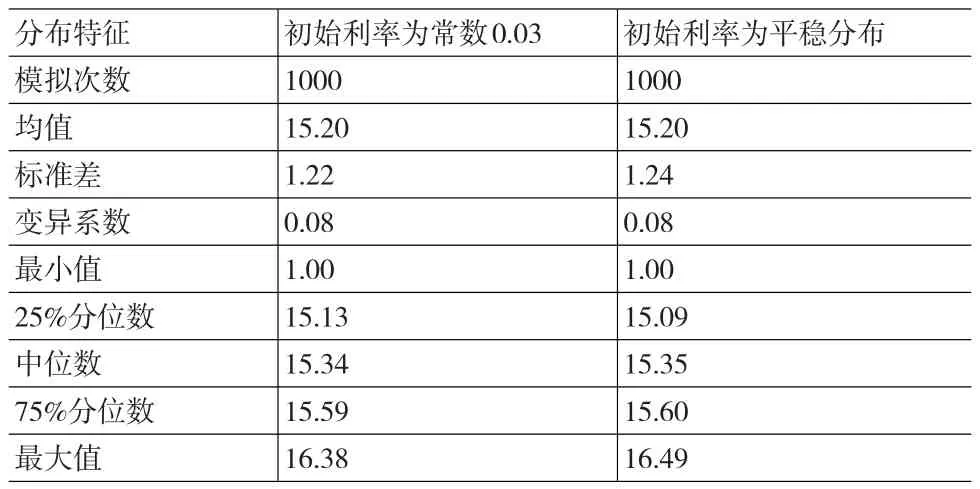
表7 兩種情況下定期生命年金現值隨機變量的概率分布的分布特征

與表6相比，兩種情況下模擬得到的定期生命年金現值隨機變量的概率分布的均值、標準差都明顯處于這三個常數利率計算的精算現值、相應的標準差的范圍內，且與利率為0.03時的精算現值、相應的標準差最為接近。另外，當初始利率為常數0.03時，若模擬次數為100次，則得到的定期生命年金現值隨機變量的均值為15.18，標準差為1.23；當初始利率為平穩分布時，若模擬次數為100次，則得到的定期生命年金現值隨機變量的均值為15.17，標準差為1.23。從一定意義上，采用100條④這里模擬100次之所以可行，是因為100次模擬可以得到100個概率分布，每個概率分布包括20個現值隨機變量的取值，共可得到2000個現值隨機變量的取值，且此時不同結果的個數已足夠多了。利率軌道對兩種情況進行模擬也是可行的。

從以上結論，初步猜測，不論初始利率如何選擇，若利率軌道數為m，則該定期生命年金現值隨機變量的取值都將以很大的概率均勻分布在m個較大的取值上。進一步注意到，在該定期生命年金的數值實例中，這個很大的概率正是npx=20p30=0.9679。正如圖4、5所示，這兩種情況模擬得到的定期生命年金現值隨機變量的概率分布也不是傳統意義上的單峰分布。從理論上講，這種分布也是存在的，可視為一類特殊的奇異分布。

4 研究結論與方法推廣

4.1 研究結論

（1）Markov鏈隨機利率模型具有易于理解、符合直觀、編程方便、能自動處理變量的不獨立性問題、模擬的利率不會取負值或較大值等優點。在R軟件下的編程實現運算時間少、效率較高。本文在R軟件算法實現中，采用了同一個“種子數”，這樣有助于進一步對兩種利率軌道的結果進行比較。

（2）兩種利率軌道模擬結果的一致性。從圖1和圖2、圖3、圖4和圖5可以看出，兩種利率假設下，基于Markov鏈隨機利率模擬的三個精算函數隨機變量相應的概率分布的圖形都很相似；同時，從表1和表3、表5、表7也可以看出，其相應的分布特征也都很接近。

（3）實際上，對Markov鏈來說，如果存在極限（平穩）分布，那么該分布不依賴于初始狀態。另外，一般來說，經過較少的轉移次數，Markov鏈即可收斂于極限（平穩）分布。很容易驗證，在本文選擇的Markov鏈的轉移概率下，不論初始狀態如何，Markov鏈在不同時刻的概率分布一般都較快地收斂到極限（平穩）分布。因此，本文三個數值實例中，初始利率為常數和初始利率的概率分布為平穩分布兩種情況得到的結論差異不大。

（4）從表1、表3可以看出，在實例1中，兩種情況下模擬得到的確定性年金現值、積累值隨機變量的概率分布的均值和中位數幾乎相同；從表5、表7可以看出，在實例2和實例3中，兩種情況下模擬得到的現值隨機變量的概率分布的均值和中位數有一定差異。這可以從確定性年金、兩全保險、定期生命年金本身的差異得到解釋。其中，確定性年金與死亡概率無關，因而每次模擬都可以得到一個確定的年金支付額，多次模擬的結果一般呈現出接近正態分布的單峰分布；而兩全保險、定期生命年金的支付額是不確定性的，受死亡概率的影響，每次模擬只能得到一個具體的概率分布，每個概率分布又包括若干個現值隨機變量，其波動性很大，多次模擬的結果一般都不能呈現出正常意義下的分布，我們將其稱為是一類特殊的奇異分布。

4.2 方法推廣

（1）本文在Markov鏈隨機利率模型假設下，應用隨機模擬方法，對精算函數隨機變量的概率分布進行了數值求解。具體地講，本文采用了兩種產生利率軌道的思路；一種是基于初始利率為常數的假設；另一種是基于初始利率的概率分布為Markov鏈的平穩分布的假設。并通過壽險精算學中的三個數值實例，分別給出了這兩種假設下模擬得到的精算函數隨機變量的概率分布以及相關的分布特征。解決這些例子的思路與方法可以推廣到精算學和金融學的進一步研究中。這是一個有待深入研究的新方向。

（2）壽險利率市場化對我國精算技術提出了很大的挑戰，將更符合市場變化規律的隨機利率模型應用到壽險公司的定價、準備金評估以及隨機資產負債管理中，具有重要的現實意義。本文對隨機利率下壽險精算中一些基本的隨機變量的概率分布進行了研究，作為后續研究，將進一步對Vasicek隨機利率模型、Cox-Ingersoll-Ross（CIR）隨機利率模型、Multiplicative Shock隨機利率模型等進行系統研究，并應用R軟件進行算法實現，以期對各種壽險產品的保費、準備金、現金價值、部分利潤指標等的變動進行分析，并進一步比較隨機利率下保險合同的價值與固定利率下保險合同的價值等。

（3）不斷更新的計算技術和日益復雜的金融市場風險，以及對金融數學認識的深入和學科交叉，促進了保險公司利率市場化的進程。進一步的研究內容是：在對隨機利率下壽險精算理論進行深入研究的基礎上，針對我國壽險業的利率市場化問題，提出可行性建議，為我國壽險利率市場化的進程提供理論支持和技術保證。

[1] Goovaerts,M.,Dhaene,J.,De Schepper,A.Stochastic Upper Bounds for Present Value Functions[J].Journal of Risk and Insurance,2000，(67).

[2] Grinstead,C.M.,Snell,J.L.Introduction to Probability(2ndEdition)[M].American Mathematical Society,1997.

[3] Bühlmann,H.Stochastic Discounting[J].Insurance:Mathematics and Economics,1992，(11).

[4] Beekman,J.A.,Fuelling,C.E.Interest and Mortality Randomness in Some Annuities[J].Insurance:Mathematics and Economics,1990，(9).

[5] De Schepper,A.,De Vylder,E.,Goovaerts,M.,Kaas,R.Interest Ran?domness in Annuities Certain[J].Insurance:Mathematics and Econom?ics,1992,11(3).

[6] Vanneste,M.,M.Goovaerts,E.Labie.The Distribution of Annuities[J].Insurance:Mathematics and Economics,1994,15(1).