周期性外力驅動甘油分子通過膜通道的機制
聶雪川,吳鋒民,周曉艷,何俊霞,馮 梅,陸杭軍
(浙江師范大學凝聚態物理研究所,浙江金華 321004)
0 引 言
細胞膜上存在著可以使水、離子及其他極性小分子選擇性地進出細胞的膜通道[1-2].甘油通道(glycerol protein ficilitator,GlpF)是大腸桿菌細胞膜上的一種水-甘油通道[3],其原子級分辨率的分子結構在實驗上已經獲得[4].文獻[5]通過受控分子動力學(Steered Molecular Dynamics,SMD)的方法獲得了GlpF的平均力勢(potential of mean force,PMF).文獻[6]在文獻[5]的基礎上,運用布朗馬達理論[7]研究了GlpF在周期性外力下定向輸運甘油分子的問題.研究表明:在非平衡擾動下甘油分子會產生向細胞外的定向流,這樣可以防止細胞過量地吸收甘油分子.但文獻[6]并沒有討論GlpF的哪些部分可以促進甘油向外流動及其各部分起怎樣的作用.本文通過將GlpF劃分為14個區域,運用Fokker-Planck方程研究了GlpF的各部分在甘油定向輸運過程中起到的作用.
1 理論及方法
甘油分子、水分子等與甘油通道(GlpF)構成了一個復雜系統,甘油分子不斷地受到水分子的隨機碰撞.甘油分子通過GlpF的輸運過程可看成沿GlpF軸線的過阻尼布朗運動,用朗之萬方程可描述為

式(1)中:γ是摩擦系數;U(x)為通道的PMF;ξ(t)是高斯白噪聲,有

式(3)中,D為擴散系數.式(1)對應的Fokker-Planck方程為
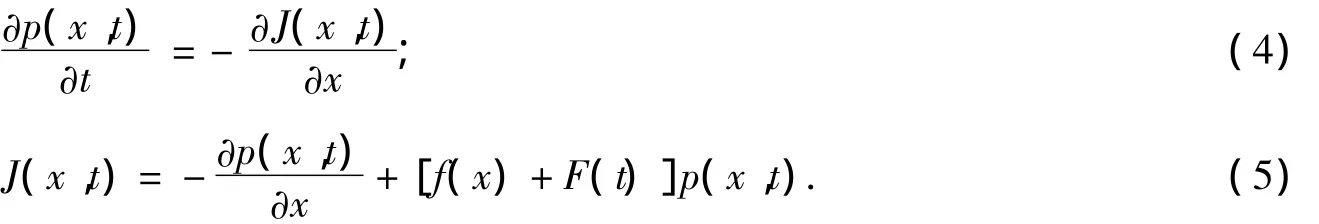
式(4)~式(5)中:p(x,t)為分子的概率密度分布;J代表幾率流(流量).式(4)~式(5)已經按照文獻[6]的方法進行了無量綱化處理.
在恒定外力下(F(t)=F0),式(1)的解為[6]

如果F(t)是周期為T的方波力且變化比較緩慢,即
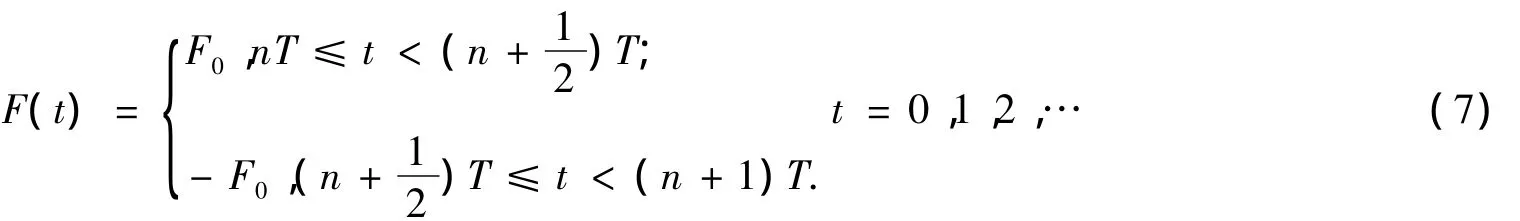
則平均幾率流為
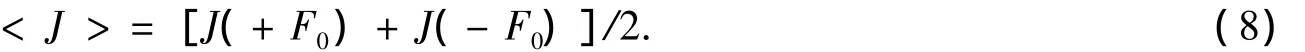
可以證明,當通道的PMF左右不對稱時,即U(x)≠U(1-x),那么J(+F0)≠-J(-F0),將會產生定向流.
2 結果與討論
GlpF左端連接著細胞外,右端連接著細胞內,其PMF分布如圖1所示.在接近左邊端口部分(圖1的2,3區)分布著2個顯著的勢阱,而在圖1的4,6,9區則分布著顯著的勢壘.可以看出,PMF的分布是不對稱的,而且比較復雜.本文假定GlpF兩側的甘油濃度相等,即沒有濃度差,甘油分子只受到周期性方波外力 F(t)的作用.由式(5)可以計算出-J(-F0)>J(+F0),即在周期性方波外力F(t)的作用下將產生向左(從細胞內到細胞外)的凈流量(見圖2).J(+F0)與J(-F0)的值隨著外力F0的增大而增大,它們的平均值<J>=[J(+F0)+J(-F0)]/2代表在外力F(t)作用下產生的凈流量.顯然,外力F0越大,凈流量<J>也就越大.
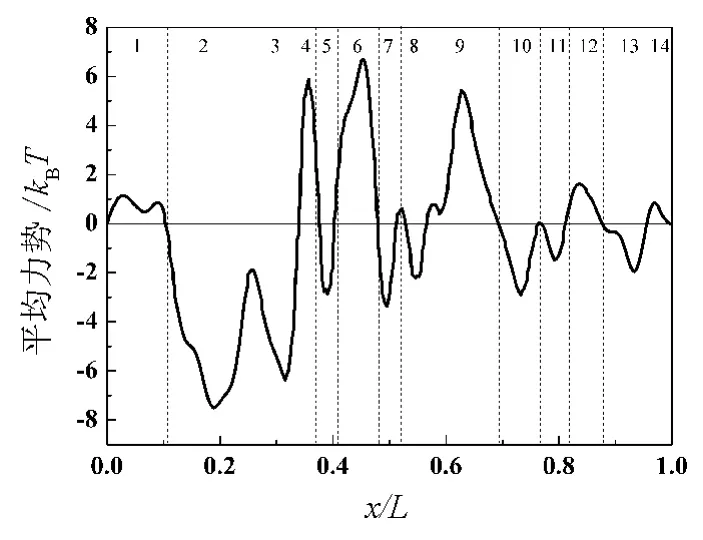
圖1 GlpF的PMF分布
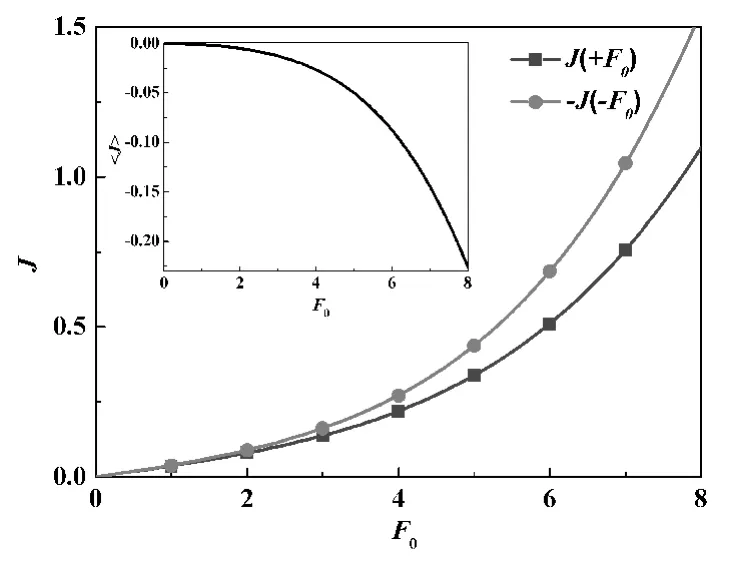
圖2 GlpF的幾率流(插圖為在周期性方波力驅動下的凈流量)
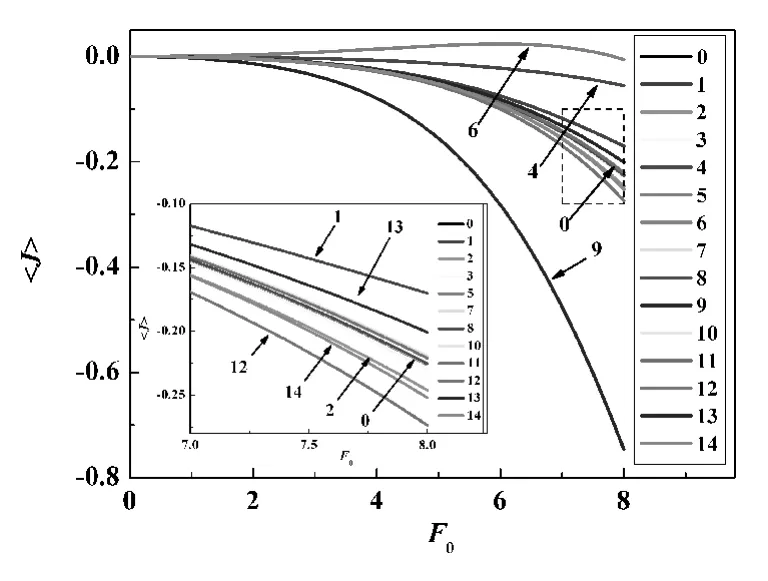
圖3 修改PMF后GlpF在方波外力作用下的幾率流(插圖為虛方框部分的放大圖)
為了研究GlpF各部分對甘油分子輸運的影響,筆者把GlpF分為14個區域,即把其PMF分成14個區域.定義PMF的2個相鄰零點之間為一個區域,每個區域只包含一個勢阱或勢壘(如圖1所示).通過抹平其中的一個區域(即令該區域的PMF為零)來研究GlpF的不同部分對甘油分子輸運的影響.如果每次只抹平其中一個區域,將得到14個修改過的新的PMF分布.接著,分別計算了14個新的PMF對應的甘油幾率流隨周期性外力的變化,其結果如圖3所示.其中曲線0為未修改的PMF對應的幾率流,其余為修改PMF之后對應的幾率流,由于抹平某些區域后幾率流變化不大,結果與曲線0幾乎重合在一起.可以看出,抹平PMF的第1,4,6和13區域后向左的定向流減小了,抹平第2,9,12和14區域后向左的定向流增大了,而抹平PMF的其他區域后的幾率流曲線很接近曲線0.其中,PMF的第4,第6和第9區域即PMF曲線中間的3個勢壘對定向流的影響非常明顯.這說明了位于GlpF中間部分的結構是使GlpF在非平衡擾動下產生定向流的關鍵,而位于GlpF兩端部分的結構對產生定向流的貢獻并不顯著.
如果將GlpF的PMF從正中間分成2部分,則上面討論的14個結果可以分為2組:將抹平左半部分的勢壘或右半部分的勢阱的結果分為一組,將抹平左半部分的勢阱或右半部分的勢壘的結果分為另外一組.第1組結果如圖4(a)所示,可以發現這些曲線位于曲線0以上,也就是向左的定向流減小了.第2組結果如圖4(b)所示,這些曲線都位于曲線0以下,也就是向左的定向流增大了.因此,PMF圖上左半部分的勢壘和右半部分的勢阱會產生向左的定向流,其中勢壘4和6對向左的定向流的貢獻最大;而左半部分的勢阱和右半部分的勢壘會產生阻礙向左的定向流,其中勢壘9對定向流的阻礙最大.所以,要想有效地產生向左的定向流,左邊應分布一些勢壘,而右邊應分布一些勢阱.
下面將討論文獻[8]提出的PMF的簡化模型(見圖5(a)),在Fokker-Planck理論下存在的不合理之處.該模型的左邊是一個勢阱,右邊是一個勢壘.把圖5(a)的PMF代入式(6)、式(8)可以計算出J(+F0)>|J(-F0)|,即在方波力驅動下將產生向右的凈流量,與文獻[6]的結果相反,見圖5(b).根據本文前面得到的結論,也可以推出該模型在周期性外力下將產生向右的定向流.通過觀察圖1中PMF曲線的分布特點,可以將該模型作如下修正:減小勢阱的寬度并整體左移,見圖6(a).圖6(b)為根據修正后的PMF計算出的幾率流,與文獻[6]的結果符合得很好.
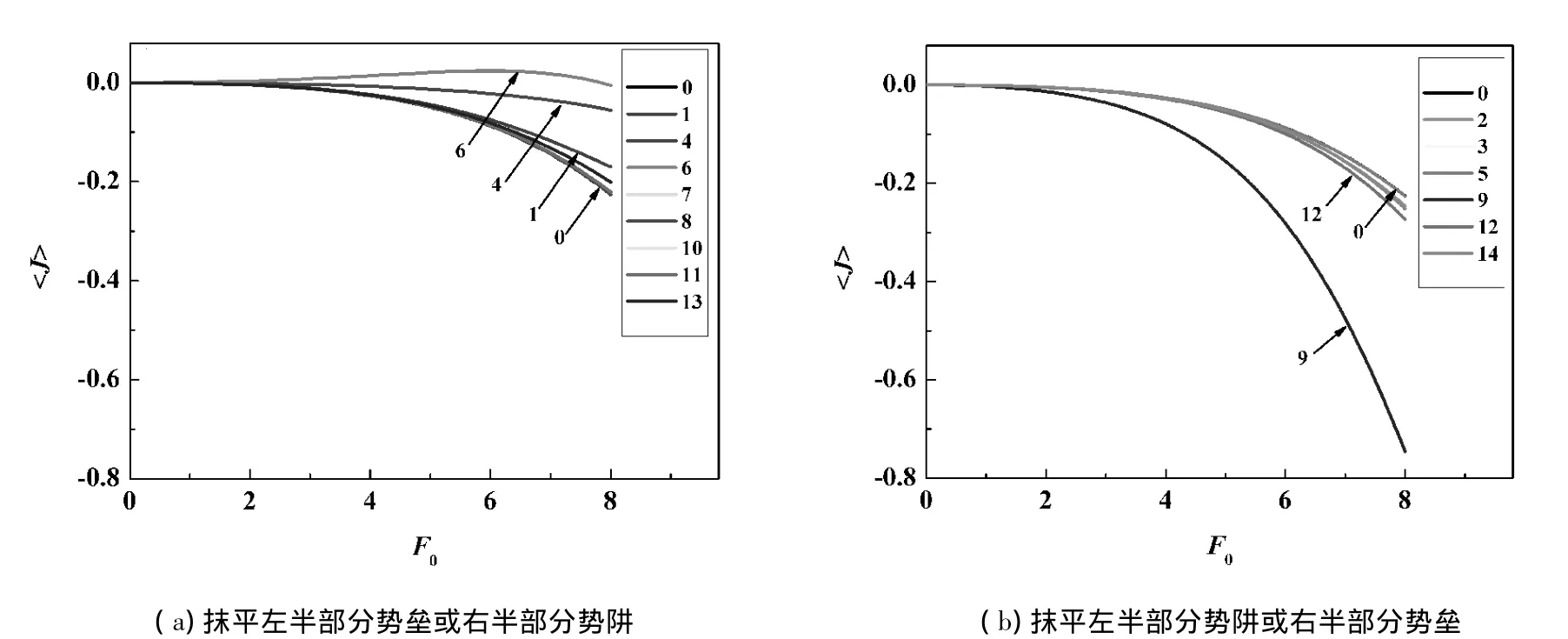
圖4 將圖3中的結果分成2組
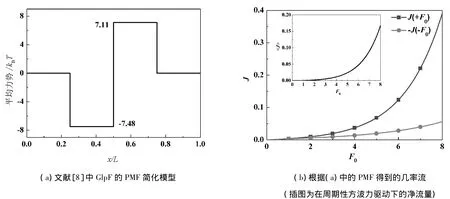
圖5 根據文獻[8]得到的結果
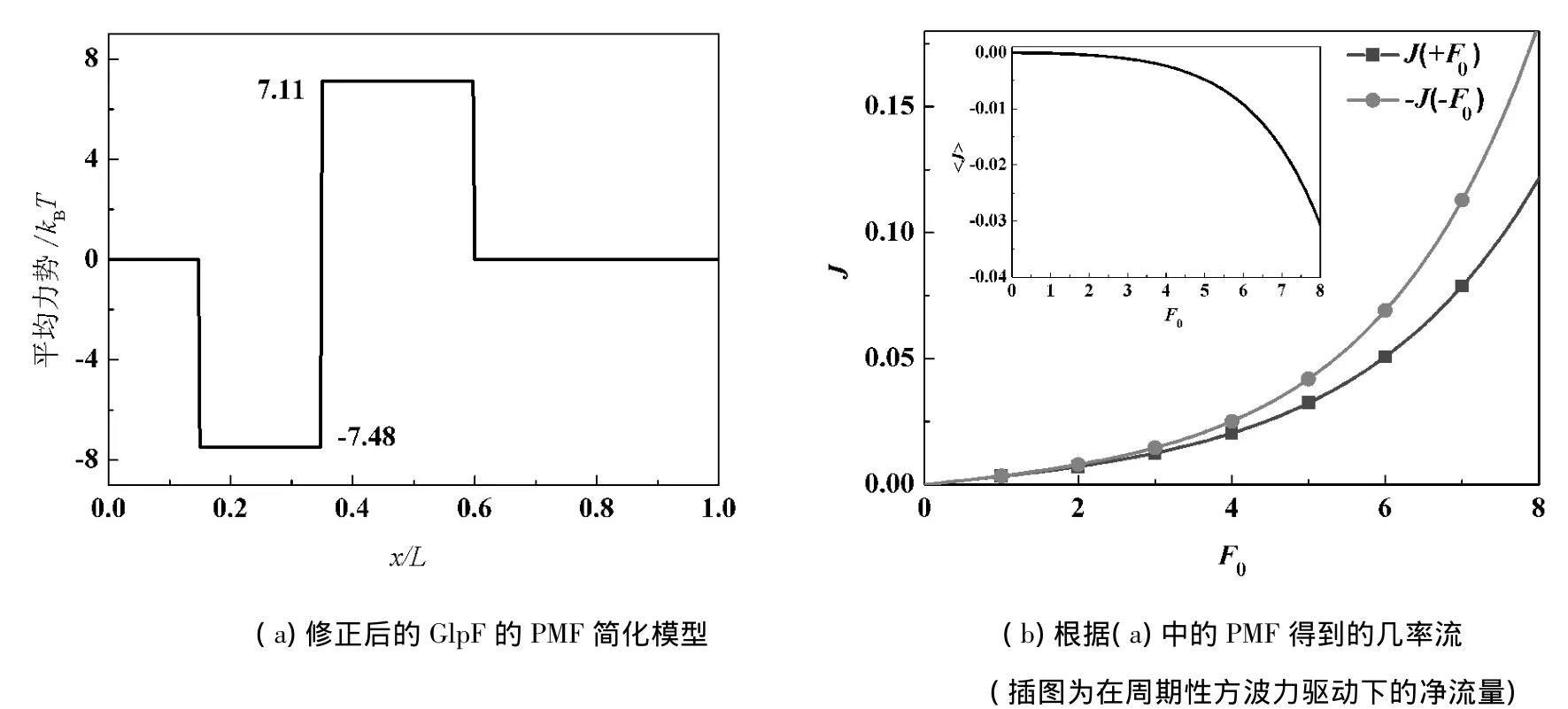
圖6 修正后的結果
因此,勢壘與勢阱的位置對定向流的方向有影響,所以在簡化模型時應充分考慮這個因素.文獻[8]的PMF簡化過程可能太過粗略,所以用Fokker-Planck理論討論時與文獻[8]的結論有矛盾.
3 結 論
依據PMF的分布將GlpF分成了14個區域用于研究哪一部分對定向流的影響比較大.計算結果表明,位于GlpF中間的幾個高勢壘區域對定向流的影響較大,而其他部分的勢壘或勢阱區域對定向流的影響相對較小.而且發現左側的勢壘和右側的勢阱是GlpF在周期性外力下能向左輸運甘油分子的關鍵,而且勢壘的位置越靠左及勢阱的位置越靠右,越有利于甘油分子向左輸運.文章的最后對Lu Deyu等提出的GlpF的PMF分布的簡化模型作了修正,這對研究膜蛋白輸運小分子的規律研究有很大的幫助.
[1]Agre P.Aquaporin water channels[J].Biosci Rep,2004,24(3):127-163.
[2]Hille B.Ionic channels of excitable membranes[M].3rd ed.Sunderland M A:Sinauer Associates,2001.
[3]Borgnia M,Nielsen S,Engel A,et al.Cellular and molecular biology of the aquaporin water channels[J].Annu Rev Biochem,1999,68(1):425-458.
[4]Fu Daxiong,Libson A,Miercke L J W,et al.Structure of a glycerol-conducting channel and the basis for its selectivity[J].Science,2000,290(5491):481-486.
[5]Jensen M O,Park S,Tajkhorshid E,et al.Energetics of glycerol conduction through aquaglyceroporin GlpF[J].Proc Natl Acad Sci USA,2002,99(10):6731-6736.
[6]Kosztin I,Schulten K.Fluctuation-driven molecular transport through an asymmetric membrane channel[J].Phys Rev Lett,2004,93(23):238102.
[7]Reimann P.Brownian motors:noisy transport far from equilibrium[J].Phys Rep,2002,361(2/3/4):57-265.
[8]Lu Deyu,Grayson P,Schulten K.Glycerol conductance and physical asymmetry of the Escherichia coli glycerol facilitator GlpF[J].Biophys J,2003,85(5):2977-2987.

