周期性電抗加載介質(zhì)結(jié)構(gòu)電磁特性的等效分析

何玉成 萬國(guó)賓 馬 鑫 王 威

（西北工業(yè)大學(xué)電子信息學(xué)院，陜西 西安710129）

引 言

周期性電抗加載介質(zhì)結(jié)構(gòu)具有較強(qiáng)的頻率選擇特性，可以用來設(shè)計(jì)低通、高通、帶通、帶阻等結(jié)構(gòu)，被廣泛應(yīng)用于雷達(dá)天線罩設(shè)計(jì)中。電抗加載，就是以阻抗匹配為準(zhǔn)則，將經(jīng)過專門設(shè)計(jì)的金屬物（金屬絲，金屬條帶或線圈等）加載到介質(zhì)中去［1］。單元的形狀、陣列的排布以及周期的大小等都會(huì)對(duì)其頻率選擇特性產(chǎn)生影響，同時(shí)加載的介質(zhì)結(jié)構(gòu)也會(huì)對(duì)頻率特性產(chǎn)生很大的影響，因此，研究周期性電抗加載介質(zhì)結(jié)構(gòu)的電磁特性分析方法對(duì)電抗加載雷達(dá)罩的優(yōu)化設(shè)計(jì)和電性能預(yù)測(cè)具有重要意義。

網(wǎng)柵加載介質(zhì)結(jié)構(gòu)的電磁特性較早的分析多采用等效電路法［2］，這種方法忽略金屬絲之間的相互影響，在網(wǎng)柵周期遠(yuǎn)遠(yuǎn)大于金屬絲直徑的情況下可以取得較好的分析效果，但隨著網(wǎng)柵周期減小其分析誤差將顯著增大；用有限元法［3－5］分析金屬絲網(wǎng)柵加載介質(zhì)結(jié)構(gòu)的電磁特性需要對(duì)導(dǎo)體橫截面進(jìn)行離散，可以較好地解決多邊形截面導(dǎo)線的加載問題，但采用分段折線代替工程中常用的圓柱導(dǎo)線截面將出現(xiàn)較大的幾何建模誤差；矩量法［6－7］求解該問題需要計(jì)算多層介質(zhì)中的格林函數(shù)并選擇恰當(dāng)?shù)幕瘮?shù)，由于格林函數(shù)與導(dǎo)線在介質(zhì)層中的嵌入深度密切相關(guān)，使得導(dǎo)線橫截面上整域基函數(shù)選擇困難甚至無法使用，而選用分域基將與有限元法一樣面臨導(dǎo)線截面的離散問題。等效方法是解決電磁問題的常用方法之一，文獻(xiàn)［8］針對(duì)縫隙天線設(shè)計(jì)中的圓方頭縫隙轉(zhuǎn)換問題分析了等周長(zhǎng)與等面積等效的效果，并對(duì)等效誤差進(jìn)行了對(duì)比分析，文獻(xiàn)［9］則針對(duì)同樣問題采用了等磁矩等效的方法。文獻(xiàn)［10］［11］分別基于基本電磁理論和仿真分析手段，研究了自由空間散射問題中金屬絲和金屬條帶的等效關(guān)系，但尚未涉及多層介質(zhì)中加載網(wǎng)柵結(jié)構(gòu)的等效問題。

本文旨在建立多層介質(zhì)中周期性加載金屬絲網(wǎng)柵和金屬條帶網(wǎng)柵結(jié)構(gòu)的等效模型，以便采用已成熟的金屬貼片加載結(jié)構(gòu)分析絲網(wǎng)模型，解決工程中常見的金屬絲網(wǎng)加載問題。文中對(duì)兩種A夾層平板結(jié)構(gòu)中周期性加載網(wǎng)柵結(jié)構(gòu)的傳輸特性進(jìn)行對(duì)比分析，在5～15GHz頻率范圍內(nèi)建立了金屬條帶寬度和金屬絲直徑之間的等效關(guān)系，研究了電磁波入射方向、介質(zhì)厚度、網(wǎng)柵周期和加載位置以及金屬絲直徑大小對(duì)等效關(guān)系的影響，驗(yàn)證了方法的準(zhǔn)確性和工程實(shí)用性。

1.等效模型的建立

如圖1所示，建立的等效模型是將金屬絲網(wǎng)柵結(jié)構(gòu)等效為金屬條帶網(wǎng)柵結(jié)構(gòu)，金屬條帶厚度為0，目的是等效后兩種網(wǎng)柵結(jié)構(gòu)的傳輸特性相同。網(wǎng)柵結(jié)構(gòu)中金屬絲直徑為d，金屬條帶寬度為w，網(wǎng)柵周期均為b，周期序列沿x和y方向。等效關(guān)系為

圖1 等效模型

式中：δeq為等效系數(shù)。

假設(shè)介質(zhì)層為均勻各向同性材料，金屬網(wǎng)柵結(jié)構(gòu)可以根據(jù)需要加載于介質(zhì)層的不同位置。電磁波的入射方向由θ和φ決定，θ為入射角，范圍為0°～90°.φ為入射面與x軸夾角，考慮絲網(wǎng)單元在φ方向上具有對(duì)稱性，取范圍為0°～90°.

入射波為一平面電磁波，表示為

式中，k為傳播矢量；r1為介質(zhì)結(jié)構(gòu)上表面入射電場(chǎng)的位置矢量。金屬網(wǎng)柵散射電場(chǎng)為

式中：G（r2，r′2）為多層介質(zhì)結(jié)構(gòu)的格林函數(shù)；Js（r′2）為金屬網(wǎng)柵表面感應(yīng)電流密度；r2為介質(zhì)結(jié)構(gòu)下表面與r1相對(duì)應(yīng)的位置矢量；r′2為導(dǎo)體表面任一點(diǎn)位置矢量。

金屬網(wǎng)柵的透射電場(chǎng)為

式中，Et（r2）為絲網(wǎng)結(jié)構(gòu)移除僅存在介質(zhì)結(jié)構(gòu)時(shí)的透射場(chǎng)。

網(wǎng)柵結(jié)構(gòu)的傳輸系數(shù)為

因等效關(guān)系引起的等效誤差為

2.等效系數(shù)的確定

基于以上等效模型，A夾層平板中加載金屬網(wǎng)柵方環(huán)單元結(jié)構(gòu)。如無特別說明則選取參數(shù)：面板的相對(duì)復(fù)介電常數(shù)εr1＝4－j0.015，厚度d1＝1mm，夾芯的相對(duì)復(fù)介電常數(shù)εr2＝1.1－j0.005，厚度d2＝5mm.

單層網(wǎng)柵結(jié)構(gòu)加載于夾芯中間z＝0處，如圖2所示。網(wǎng)柵周期b＝10mm，金屬絲直徑d＝0.4 mm.

圖2 單層加載網(wǎng)柵平板結(jié)構(gòu)

在自由空間電磁散射問題中，文獻(xiàn)［10］基于電磁場(chǎng)基本理論提出單一金屬條帶和金屬絲直徑的散射等效系數(shù)為2；文獻(xiàn)［11］則通過實(shí)物測(cè)試和仿真分析給出了周期性排列的金屬條帶和金屬絲直徑在間距小于1.5λ時(shí)等效系數(shù)約為1.89.針對(duì)導(dǎo)體網(wǎng)柵加載多層介質(zhì)結(jié)構(gòu)的電磁散射問題，采用仿真計(jì)算的方法，對(duì)上述兩種等效系數(shù)以及等周長(zhǎng)等效［8］系數(shù)δeq＝π/2進(jìn)行對(duì)比。圖3給出了正投射時(shí)三種等效方法的對(duì)比，可以看出：等效系數(shù)為δeq＝π/2的金屬條帶加載結(jié)構(gòu)與金屬絲網(wǎng)柵加載問題的傳輸系數(shù)曲線的吻合效果明顯優(yōu)于前兩種等效系數(shù)。

圖3 三種不同等效方法傳輸系數(shù)對(duì)比

3.等效模型的分析

基于上述等效系數(shù)，利用三維電磁仿真軟件（HFSS）對(duì)A夾層平板結(jié)構(gòu)中加載單層和雙層網(wǎng)柵結(jié)構(gòu)的傳輸特性進(jìn)行仿真分析，并考察等效模型的等效效果。

3.1 單層網(wǎng)柵加載結(jié)構(gòu)

對(duì)以上建立的單層加載網(wǎng)柵結(jié)構(gòu)模型分別討論電磁波入射方向、介質(zhì)厚度、網(wǎng)柵周期和加載位置以及金屬絲直徑大小對(duì)等效的影響。

1）電磁波入射方向

電磁波不同方向入射時(shí)兩種網(wǎng)柵結(jié)構(gòu)傳輸系數(shù)的對(duì)比如圖4所示。可以看出：入射角θ變化對(duì)透波特性會(huì)有一定的影響，而透波特性隨著φ變化幾乎沒有影響。兩種網(wǎng)柵結(jié)構(gòu)的傳輸曲線吻合非常好，等效關(guān)系不依賴于電磁波入射方向。

2）介質(zhì)層厚度

圖5給出了介質(zhì)厚度變化時(shí)兩種網(wǎng)柵結(jié)構(gòu)的傳輸系數(shù)對(duì)比情況。可見，兩種網(wǎng)柵結(jié)構(gòu)的傳輸曲線是相當(dāng)吻合的，等效關(guān)系適用于不同厚度的介質(zhì)層。隨著介質(zhì)厚度的增加，傳輸效率會(huì)明顯降低，傳輸系數(shù)極大值會(huì)向低頻移動(dòng)。

3）網(wǎng)柵周期

不同周期網(wǎng)柵結(jié)構(gòu)的傳輸系數(shù)對(duì)比情況如圖6所示。觀察發(fā)現(xiàn)，隨著周期的增大，會(huì)明顯出現(xiàn)振蕩，但變化趨勢(shì)完全相同。值得注意的是：在非振蕩頻率處等效誤差明顯降低，可見周期越大等效效果越明顯。

4）網(wǎng)柵加載位置

圖7顯示了網(wǎng)柵加載位置對(duì)兩種結(jié)構(gòu)傳輸系數(shù)一致性的影響。可以看出：等效關(guān)系也不依賴于加載位置的變化，但隨著網(wǎng)柵加載位置向面板移動(dòng)，傳輸效率會(huì)稍有降低，同時(shí)會(huì)出現(xiàn)明顯的抖動(dòng)。

5）金屬絲直徑

圖8表明了加載不同金屬絲直徑網(wǎng)柵結(jié)構(gòu)的傳輸系數(shù)比較。可以看出：隨著直徑的增大，傳輸效率會(huì)明顯降低，等效誤差有所增大。直徑為1.0mm的算例在偏離中心頻率10GHz較遠(yuǎn)處表現(xiàn)出了等效誤差的存在。

當(dāng)金屬絲直徑d∈ ［0.7，1.0］時(shí)，可以采用等效系數(shù)的經(jīng)驗(yàn)公式進(jìn)行修正，其中金屬絲直徑d＝1.0mm時(shí)的修正效果如圖8所示。

3.2 雙層網(wǎng)柵加載結(jié)構(gòu)

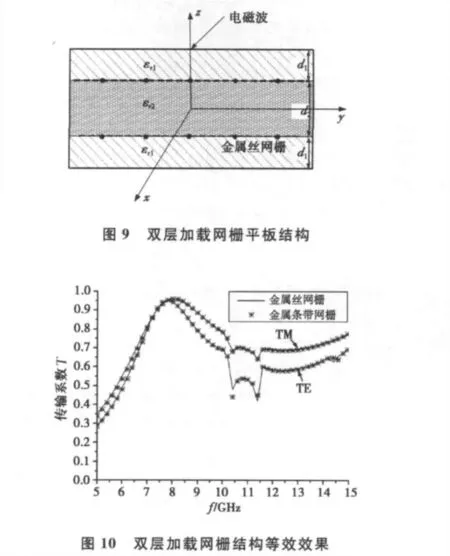
A夾層平板中加載雙層網(wǎng)柵結(jié)構(gòu)，網(wǎng)柵加載于面板與夾芯界面，如圖9所示，其它模型參數(shù)均與前述單層網(wǎng)柵加載算例相同，電磁波入射方向θ＝30°，φ＝30°.傳輸特性曲線如圖10所示，可以看出：上述等效方法同樣適用于雙層導(dǎo)體網(wǎng)柵加載結(jié)構(gòu)的傳輸特性分析。

4.結(jié) 論

在5～15GHz頻率范圍內(nèi)研究了周期性金屬絲網(wǎng)柵加載A夾層結(jié)構(gòu)的電磁特性分析方法，針對(duì)工程中常用的細(xì)導(dǎo)線（d≤1mm）絲網(wǎng)加載介質(zhì)結(jié)構(gòu)進(jìn)行了仿真分析，得到以下結(jié)論：

1）網(wǎng)柵導(dǎo)線直徑較小時(shí)金屬條帶寬度為金屬絲直徑的π/2倍，遵循等周長(zhǎng)等效原則，隨著導(dǎo)線直徑增大，等效誤差有所增大；

2）介質(zhì)層厚度、網(wǎng)柵加載位置、以及電磁波的入射方向?qū)Φ刃?shù)影響較小；

3）加載絲網(wǎng)結(jié)構(gòu)中的導(dǎo)線直徑增大導(dǎo)致的傳輸系數(shù)計(jì)算誤差可以通過等效系數(shù)的經(jīng)驗(yàn)公式予以修正。

［1］劉曉春.機(jī)載雷達(dá)罩的壁結(jié)構(gòu)及其新發(fā)展［J］.飛機(jī)設(shè)計(jì)，1998，19（1）：13－23.LIU Xiaochun.Radome structure and new development of airborne radar［J］.Aircraft Design，1998，19（1）：13－23.（in Chinese）

［2］WAIT J R.The impedance of a wire grid parallel to a dielectric interface［J］.IRE Transactions on Microwave Theory and Techniques，1957，5（2）：99－102.

［3］徐 歐，徐金平，劉曉春.多層介質(zhì)金屬條帶電抗加載平板結(jié)構(gòu)透波特性分析［J］.微波學(xué)報(bào)，2008，24（3）：28－32.XU Ou，XU Jinping，LIU Xiaochun.Transmission property analysis of reactance－loaded stratified dielectric slabs sandwiched by metal stripes［J］.Journal of Microwaves，2008，24（3）：28－32.（in Chinese）

［4］PELOSI G，F(xiàn)RENI A ，COCCIOLI R.Hybrid technique for analyzing scattering from periodic structures［J］.IEE Proceedings－H，1993，140（2）：65－70.

［5］丁大志，宛 汀，甘 輝，等.一種分析準(zhǔn)周期結(jié)構(gòu)散射問題的有限元區(qū)域分解算法［J］.電波科學(xué)學(xué)報(bào)，2009，24（4）：735－741.DING Dazhi，WAN Ting，GAN Hui，et al.A domain decomposition method for finite element solution of scattering problems of the quasi－periodic structures［J］.Chinese Journal of Radio Science，2009，24（4）：735－741.（in Chinese）

［6］RUBIN B J，BERTONI H L.Reflection from a periodically perforated plane using a subsectional current approximation［J］.IEEE Transactions on Antennas and Propagation，1983，31（6）：829－836.

［7］JIN J M，VOLAKIS J L.Electromagnetic scattering by aperfectly conducting patch array on a dielectric slab［J］.IEEE Transactions on Antennas and Propagation，1990，38（4）：556－563.

［8］李 龍，張 玉，梁昌洪.波導(dǎo)寬邊縫隙天線的改進(jìn)共形FDTD分析［J］.電子學(xué)報(bào)，2003，31（6）：860－863.LI Long，ZHANG Yu，LIANG Changhong.A modified locally conformal finite－difference time－domain technique for a slot antenna in a rectangular waveguide broadwall［J］.Acta Electronica Sinica，2003，31（6）：860－863.（in Chinese）

［9］COHN S B.Determination of aperture parameters by electrolytic－tank measurements［J］.Proceedings of the IRE，1951，39（11）：1416－1421.

［10］BULTER C M.The equivalent radius of a narrow conducting strip［J］.IEEE Transactions on Antennas and Propagation，1982，30（4）：755－758.

［11］RAJAGOPALAN H，MIURA A，RAHMAT－SAMII Y.Equivalent strip width for cylindrical wire for mesh reflector antennas：experiments，waveguide，and plane－wave simulations［J］.IEEE Transactions on Antennas and Propagation，2006，54（10）：2845－2853.