注重基礎考查 凸顯能力立意——2012年新課標全國高考數學試卷評析

☉廣東省深圳市方亞斌名師工作室 方亞斌（特級教師）

一、命題特點

2012年新課標全國高考數學試卷以《課程標準》、《考試大綱》及《考試說明》為命題依據，遵循“穩中有變、立足基礎、突出能力、銳意求新”的指導思想，體現“大穩定、小創新、重運算、考思維”的穩健、成熟試題設計理念，寬視角、多視點、有層次地考查考生的數學素養和學習潛能.它具有重基礎、圖創新；講傳承、保穩定；顧全局，求綜合；重思維，考能力等特點，是一套有較高的信度、效度、必要的區分度和適當的靈活度的可圈可點的試卷，有利于中學數學教學和課程改革，有利于高校選拔有學習潛能的新生.今年高考，全國共有10個省（自治區）（豫、黑、吉、瓊、晉、冀、新、滇、寧、蒙）使用了這套試題.試題對高中數學教學所起到的指導和導向作用，是深刻且長遠的.

1.覆蓋全面 題型穩定

試卷基本涵蓋了《考試大綱》所規定的內容，傳統內容的三大板塊函數（包括三角函數、數列、不等式）、幾何（包括解析幾何、立體幾何）、概率統計占分值文理科均在80%左右.對新增內容的考查與去年比重相當（三個小題與一個大題，27分），重點考查算法、三視圖、復數與數系擴充、概率與統計等知識點（參見如理科的第3、6、7、15、18題，文科第2、3、6、7、18題）.對于其他非主干知識點也注意適度考查，如第1題、第2題、第3題則分別考查了集合、排列組合、復數等知識點.文理試卷選考內容題目相同，幾何證明選講主要圍繞圓與相似形中有關定理命題，坐標系與參數方程考查了點的極坐標與普通坐標互化，橢圓的參數方程和圓的極坐標方程等知識點，不等式選講考查了絕對值不等式求解及不等式恒成立問題的處理方法.題型保持穩定，第1題到第12題是選擇題，每題5分，第13題到第16題是填空題，每題5分，第17題到第21題是解答題，每題12分，第22題到第24題以“三選一”的模式出現，每題10分.解答題方面有一個變化，去年第17題考查的是數列，今年第17題考查的是三角函數與解三角形，恢復了傳統意義上大體分布規律.

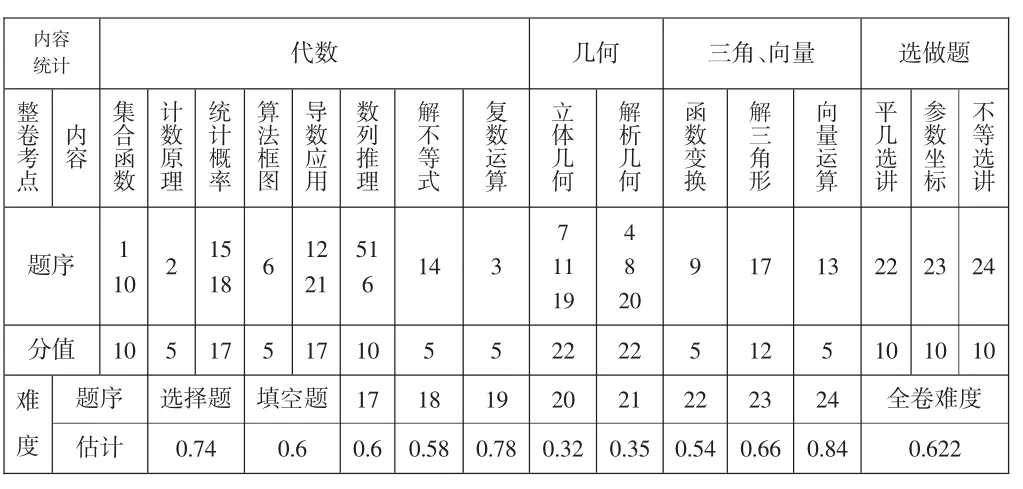
表1 ：理科試卷考點內容統計難度評估

表2 ：文科試卷考點內容統計難度評估內容

2.突出主干 強化能力

2012年新課標全國高考數學試卷既考查全面又突出重點，主干知識考查穩定函數（包括三角函數、數列、不等式）、幾何（包括解析幾何、立體幾何）、概率統計依然是今年高考的三大考點.解答題依然以三角、概率統計、立體幾何、解析幾何、數列、函數和導數為背景，主干突出的效應明顯.如理科試題，重點考查函數與導數（36分）、立體幾何（22分）、解析幾何（27分+10分，含選答題）、概率與統計（17分）.

試卷重視對數學思想方法的考查.如理科第4、9、10、12、14、20、24題，文科第4、5、8、10、11、20題等考查了數形結合的思想；理科第4、5、8、11、12、13、17、20、21、23題，文科第10、14、15、17、21、24題等考查了函數與方程的思想；理科第11、12、16、21題，文科第11、16、19、20、21、23題等考查了轉化與化歸的思想；理科第1、2、16、21、24題，文科第13、21、24題等考查了分類與整合的思想.

試卷加強對“五個能力”尤其是運算能力的考查.2012年高考考綱明確指出，運算能力包括分析運算條件，探究運算方向，選擇運算公式，確定運算程序等一系列過程中的思維能力，也包括在實施運算過程中遇到障礙而調整運算的能力，整套試卷對運算求解能力的要求很高，運算能力與運算手段決定了考試的成敗.如理科的第12、16、21、24題，文科的第12、16題，這幾個題優秀的算法比常規算法要節省很多時間；理科第7、11、19題，文科第7、8、19題考查空間想象能力；理科第5、6、11、15、18題，文科第3、6、12、18等題重點考查數據處理能力，第15題和第18題對數據處理意識要求比去年高；理科第16、18、21、22題，文科第4、11、20、22等題考查推理論證能力；理科第9、16題，文科第12、16題考查抽象概括能力.此外，理科第18、20、21、23題，文科第3、6、18等題綜合考查了多種思維能力.

3.強調應用 凸現創新

貫徹新課標理念，加強應用意識，這是高考命題的趨勢.從2012年新課標高考全國數學理科試題來看，應用題的層次逐漸提高.如何“用數學”——用好公式、圖表、數據、程序、結論，如何使得解決問題的過程更貼近實踐中探究的過程——閱讀數學問題，畫出圖形幫助思考，選擇適當的單位，建立正確的模型，再運用理論知識解決問題，得出符合實際的結論，這是需要重視的.每一個環節都可能成為考試中的考點，在復習中要加強這方面的訓練.試卷應用意識要求比去年高，如理科第（7）題三視圖，利用坐標紙設計題目，非常貼近生活.理科第15題（考查正態分布、概率計算）相比2011年的第4題不論從知識還是能力上都高一個檔次，文理第18題關于統計概率的題來源于生活實際，這道題與2011年的第19題在形式上類似，但對閱讀理解與轉化要求比去年的第19題要高.

試題非常重視對考生的創新意識的考查，注重對未來繼續學習能力的考查.試題的創新性首先體現在選材新，解答題個個背景新穎，如理科18題，20題，23題等；其次注重立意新，如理科12題、理科16題（文科12題）、文科16題、文、理科的21題、理科選修24題都為學生提供了展示創新思維的平臺，這也是多數考生感覺今年數學試卷難的關鍵所在，也是試卷區分度高的保障.

4.文理差異 姊妹設計

今年文科、理科試卷差距較以往縮小，文科與理科的選擇填空題目中共有6道是完全一樣的，且理科的第16題為文科的第12題，解答題中，理20（與文20）及三選一是完全相同的題目，理科17、18、19與文科的17、18、19均是“姊妹題”選材、難度差異也很大.相同試題的素材主要集中在思維層次較低的知識上，不同題一方面是取自知識要求差異部分，另一方面是在相同知識載體上，設計不同思維層次、不同能力要求的試題.如文理第18題是一個關于統計概率的題，與生活實際貼得很近，文理科第一問一樣，要求計算經營利潤，是個分段函數，第二問文科考查的是平均數與互斥事件有一個發生的概率（不同于以往模擬題中大量出現的古典概型或是幾何概型），理科考查離散型隨機變量的分布列、期望及方差.

5.題在書外 根在書中

部分題目“源于教材，高于教材”，做足教材文章（這里的“教材”是指人教版普通高中課程標準實驗教科書），理科第2題是《數學2-3》（選修）第28頁第15題改編而成的，文科第2題和理科第3題是《數學1-2》（人教版）第63頁第1（2）題變形，理科第13題是《數學4》（人教版）第119頁第13題的變式，理科第14題是《數學5》（人教版）第91頁第1（2）題的變式，理科第15題是《數學2-3》（人教版）第75頁習題A組第2題的變式，文科第3題來自《數學1-2》（人教版）第8頁第3題.“題在書外，根在書中”，顯示高考命題規避資料規避題型的命題導向，這對正確引導中學數學教學起到良好的促進作用.

二、建議與商榷

命題是一門遺憾的藝術，結合2012年新課標全國試題，從更高的標準與社會的期望出發，提出以下建議，僅供參考.

（1）個別文科題有“超綱”之嫌.如文科的第3題出了相關系數的概念，而這個概念只在普通高中課程標準實驗教科書《數學3》（必修，人教版）課本92頁的“閱讀與思考”中出現過，在考試大綱和考試說明中均未提及.文理第20題綜合考查了拋物線的標準方程、焦點、準線、定義及直線與拋物線的位置關系以及圓的有關平面幾何知識與圓的標準方程性質，能很好地考查理科生的數學能力，但是文科考試大綱及考試說明對“拋物線的定義、幾何圖形和標準方程及其簡單的幾何性質”都是了解的內容，作為大題來出且是和理科同等的位置，有點出乎意料，難為文科考生了.

（2）文理選做題應該有區別設計.考慮到高中階段文科和理科所使用的選修教材內容不同，選修課時不同，考試的要求不同，體現在高考的選做題（題）上也應有所不同.

（3）模型思想、類比推理、歸納推理試題中應該有所涉及.

（4）個別試題表述欠規范.如第21題，未指出a為實數等.

三、啟示與導向

1.“主干”必須得以扎實掌握

高考中考查的數學主干知識基本是穩定的，常態的教學應該而且必須立足于“知識的廣覆蓋”及扎實掌握，才能立于不敗之地.

2.“基礎”必須得以構筑夯實

送分題、基礎題不太多是近年來數學高考的主格調，要讓學生取得恰當相稱并略有提升的成績，就應關注基礎.既要引導學生掌握好新教材中的新內容，又要引導學生掌握好舊的內容，不管是文科數學，還是理科數學，要更加關注于數學的基礎知識，只有扎實基礎的構筑和夯實，才能形成連通創新的通道.

3.“能力”必須得以全面發展

在教學備考時，我們需要經常拷問自己：對考綱要求的五種基本能力，我們為學生做了些什么，學生的現狀如何.譬如，關于考生計算能力有所弱化的話題，幾乎是每年都提及的問題.反觀我們的教學，是不是我們平時的教學在運算技能還沒有落實，是不是復習往往就異化成為講解題過程或尋找求解思路，僅僅走過場，流于形式？所以，我們一定要讓學生堅持：將運算進行到底，切不可自認為會做了，而輕視所謂簡單的、重復的勞動.至少在計算器能帶進高考考場之前，我們只能這樣，而且我們也知道學生的許多技能其實就是練出來的，不是教師講出來的.此外，還應該重視閱讀理解、數學表達等能力的培養.閱讀理解其實就與學生的自主學習對應，而數學表達通向理性思維.每年的試卷從符號、圖表、數式，還是行文敘述、新定義情景問題，對學生在準確理解、恰當表達方面要求較高，客觀上要求考生具備完整準確的閱讀理解能力和較流暢的數學表達能力.