撥云見日，細說函數定義域

☉江蘇省沭陽高級中學 周海勇

函數是中學數學最基本的內容，函數的數學思想貫穿整個高中數學學習的始終，定義域是函數“三要素”（定義域、值域、對應法則）之一，是函數最本質的特征.在解決問題的過程中，如果忽視函數的定義域，常常會事倍功半，甚至誤入歧途，在求函數解析式時，必須考慮函數的定義域，否則所求函數關系式是不完整的.下面就對求函數定義域的方法進行分類說明，希望對大家在教學中引導學生解決與定義域有關的問題時有所幫助.

題型一：由解析式確定函數的定義域

當函數是由解析式給出時，則其定義域是使解析式有意義的自變量的取值集合.也就是：（1）若f（x）為整式函數，則定義域為全體實數；（2）若f（x）為分式函數，則分母不能為0；（3）若f（x）為偶次方根，則被開方數不小于0；（4）若f（x）=x0，則定義域為｛x|x∈R，且x≠0｝；（5）在解決實際問題時，自變量的取值要有實際意義等.

分析：根據函數式子的特點，要求偶次根式下被開方數是非負數，分式的分母不為0；x0要有意義，即其中的自變量x不能為0.

點評：求函數定義域就是求使函數解析式有意義的自變量取值的集合，一般可通過解不等式或不等式組完成.當一個函數是由兩個或者兩個以上的式子的形式構成時，那么它的定義域是使每個式子有意義的集合的交集.

題型二：復合函數的定義域

如果函數y=f（t）的定義域為A，函數t=g（x）的定義域為D，值域為C，則當C?A時，稱y=f［g（x）］為f與g在D上的復合函數，其中t叫中間變量，t=g（x）叫內函數，y=f（x）叫外函數.復合函數的定義域由外函數的定義域、內函數的值域以及內函數的定義域共同確定.

1.已知函數f（x）的定義域，求函數y=f［g（x）］的定義域

分析：求滿足不等式a≤g（x）≤b的x的取值范圍即可.

例2設函數f（x）的定義域為［0，1］，則函數f（2x）的定義域是________.

解：依題意，有：

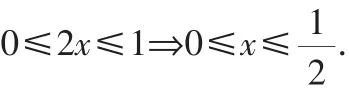
2.已知函數f［g（x）］的定義域，求函數f（x）的定義域

分析：由已知a≤x≤b，求g（x）的值域，即為f（x）的定義域.

變式1：已知函數g（x）=f（3-2x）的定義域為［-1，2］，則函數f（x）的定義域為_____.

解：g（x）的定義域為［-1，2］.

即-1≤x≤2.

所以-1≤3-2x≤5.

即f（x）的定義域為［-1，5］.

3.已知函數f［g（x）］的定義域，求函數f［h（x）］的定義域

分析：先由y=f［g（x）］的定義域求出f（x）的定義域，再由f（x）的定義域求f［h（x）］的定義域.

變式2：已知函數f（x+1）的定義域為［-2，3］，求f（2x-2）的定義域.

解：f（x+1）的定義域為-2≤x≤3.

令t=x+1，則-1≤t≤4.

故f（t）的定義域為-1≤x≤4.

點評：（1）對于復合函數f［g（x）］而說，如果函數f（x）的定義域為A，則f［g（x）］的定義域是使得函數g（x）∈A的x的取值范圍.（2）如果f［g（x）］的定義域為A，則函數f（x）的定義域是函數g（x）的值域.

題型三：由實際問題確定函數的定義域

在解決函數實際應用題時，要考慮結合實際問題，其定義域的確定不僅要考慮解析式有意義，還要注意問題的實際意義對自變量的限制（如長度、面積必須大于0，人必須為自然數等）.

例3 甲、乙兩地相距skm，汽車從甲地勻速行駛到乙地，速度不得超過ckm/h.已知汽車每小時的運輸成本（以元為單位）由可變部分和固定部分組成：可變部分與速度v（km/h）的平方成正比，且比例系數為b；固定部分為a元.把全程運輸成本y（元）表示為速度v（km/h）的函數，并指出這個函數的定義域.

分析：先建立函數關系，根據函數的關系式以及速度v的實際意義確定函數的定義域.

故函數的解析式有意義得到v≠0，由自變量v的實際意義得到v＞0，由題目的限制條件“速度v不得超過ckm/h”得到v≤c.

所以函數的解析式及其定義域為

點評：在解決關于函數的實際應用問題時，一定要注意研究并寫明函數的定義域，否則扣分是比較多的.這是因為作為解答題的這類題型，往往還要考查函數的其他性質.如果函數的定義域出錯了，那么在此基礎上研究出來的函數的其他性質也就不一定正確了.這一點我們要加倍注意，并形成重視函數定義域的良好意識與習慣.

總之，函數的定義域是求解函數的一切問題的基礎，解決函數的一切問題必須認真考查函數的定義域，學會并掌握求函數的定義域的常用方法是學習好函數的基礎.