中考中開放探究型問題解讀
☉浙江寧波市北侖區梅山中學 王 浩
開放探究型問題具有較強的綜合性與創造性,既能考查同學們對基礎知識的掌握,又能反映同學們對知識內容的拓展、聯想應用能力和開發創造能力,培養同學們的發散思維能力和空間想象能力,同時體現了同學們學習的自主性,成為考試中的熱點內容.筆者對開放性問題的幾種類型做了一個歸納,希望能給同學們的學習帶來幫助.
一、條件開放探究類型
條件開放類問題一般給出部分條件和結論,添加適當條件可以推論出結論.要求同學們能全面理解題目的知識背景,探究結論成立的條件,往往滿足的條件不唯一.
例1 如圖1,△ABC中,CD⊥AB,垂足為D.下列條件中,能證明△ABC是直角三角形的有__________(多選、錯選不得分).
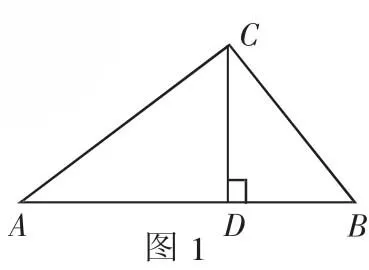

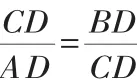
點評:條件開放探究型問題一般難度不大,但有一定開放度,所以在探究結論成立的條件時,答案可能不唯一,思維的方向是多角度的.本題中是從直角三角形的定義、勾股定理的逆定理和相似三角形性質三個角度來進行設計問題,這樣的問題可以培養同學們的發散思維能力和綜合應用知識的能力.
二、結論開放探究類型
結論開放探究類型問題特點是題設中給出全部條件,要求同學們能分析條件并探究由所給條件猜想出可以得出哪些結論,并證明所猜想的結論是否正確.由于所要證明的目標不明確,要求同學們具有綜合分析判斷能力和科學的推斷論證能力.
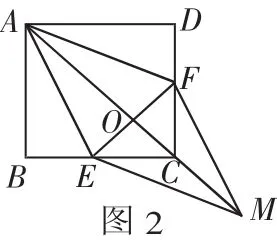
例2 已知:如圖2,在正方形ABCD中,點E、F分別在BC和CD上,AE=AF.
(1)求證:BE=DF.
(2)連接AC交EF于點O,延長OC至點M,使OM=OA,連接EM、FM.判斷四邊形AEMF是什么特殊四邊形,并證明你的結論.
分析:問題(1)中,可通過Rt△ABE與Rt△ADF全等證明BE=DF;在問題(2)中,根據條件和正方形的性質,可以得到OE=OF,OA=OM,所以四邊形AEMF是平行四邊形.又AE=AF,可根據菱形的判定得出四邊形AEMF是菱形.
解:(1)因四邊形ABCD是正方形,則AB=AD,∠B=∠D=90°.
因AE=AF,所以Rt△ABE≌Rt△ADF,所以BE=DF.
(2)因四邊形ABCD是正方形,
則∠BCA=∠DCA=45°,BC=DC.
因BE=DF,所以BC-BE=DC-DF,即CE=CF.則OE=OF.
因OM=OA,所以四邊形AEMF是平行四邊形.
因AE=AF,所以平行四邊形AEMF是菱形.
點評:結論開放類型問題探究問題的目標不具體,要求同學們能結合條件作出科學的猜想和論證.本題問題(2)中以正方形圖形為知識載體創設問題探究環境,猜想的過程中也是論證與推理的統一過程.從圖形中不難發現四邊形AEMF是菱形,接下來要聯系條件與第(1)問題結論進行論證.
三、條件與結論全開放探究類型
一個問題中條件與結論同時開放時,問題的開放度較大,對同學們能力水平要求較高,能從所給選項中組織條件,創設問題并能解決問題.
例3 如圖3,點D,E在△ABC的邊BC上,連接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三個等式中的兩個作為命題的題設,另一個作為命題的結論,構造三個命題,并回答下列問題:
(1)構造的命題是(用序號表示)______;
(2)以上三個命題是真命題的為
(直接作答)__________;
(3)請選擇一個真命題進行證明
(先寫出所選命題,然后證明).
分析:本題中有三個選項,由其中兩個作為條件.第三個作為結論,共有3種組合方法,即(1)①②?③;①③?②;②③?①;所組合的三個命題都是真命題.在命題(1)中,條件是AB=AC,AD=AE,說明△ABC,△ADE都是等腰三角形,可以通過證明△ABD,△ACE全等,得到BD=CE;在命題(2)中,條件是AB=AC,BD=CE,所以△ABC是等腰三角形,所以有∠B=∠C,可證明△ABD,△ACE全等得到AD=AE;在命題(3)中,條件是AD=AE,BD=CE,所以有∠ADB=∠AEC,所以△ADB≌△AEC,可證AB=AC.
解:(1)①②?③;①③?②;②③?①;
(2)(1)①②?③;①③?②;②③?①;
(3)證明命題(1).
因AB=AC,則∠ABC=∠ACB.
因AD=AE,則∠ADC=∠AEB,則∠ADB=∠AEC.
在△ABD與△ACE中,AB=AC,∠ABC=∠ACB,∠ADB=∠AEC,則△ABD≌△ACE,則BD=CE.
點評:條件與結論同時開放問題的開放度較大,要求同學們能對所有的選項進行組合,構建問題并能推理認證.本問題中,主要依據三角形的全等來證明線段的相等,不同的構造方法證明方法也不一致,所構造的三個命題全是真命題.
開放探究型問題題型設計靈活,問題所涉及知識面廣,要求同學們具有較強的解題能力和思維能力,所以此類題目已成為近年來中考試題的熱點題.