觀解一類不等式組問題

☉高曉兵 黃永秋

1.廣西北部灣職業(yè)技術(shù)學(xué)校 2.廣西浦北縣第六中學(xué)

江就好老師在《初中數(shù)學(xué)教與學(xué)》2011年第6期上發(fā)表的文章《例談用數(shù)形結(jié)合法解一類不等式組問題》，通過幾個實例較詳細(xì)地介紹了不等式組的數(shù)軸解法，具有較好的數(shù)學(xué)思想性和可操作性，但它須經(jīng)歷“作圖、看圖、表達(dá)”三個環(huán)節(jié)，三個環(huán)節(jié)緊密相聯(lián)，不容失誤，然而在細(xì)細(xì)品讀之后，發(fā)現(xiàn)數(shù)軸法的求解過程比較復(fù)雜，尤其對于含參情形，學(xué)生并不能很好地掌握.在深入研究數(shù)軸法的觀察及表達(dá)習(xí)慣，全面總結(jié)不等式組的基本特征后，筆者歸納出一種全新的方法——觀解法，對于江老師文中所給例題，能做到輕松快捷且準(zhǔn)確地求解，當(dāng)然更復(fù)雜的情形，此法依然快捷自如.下面就簡要介紹一些基本思想與具體的思路，同時通過幾個例題向大家介紹此法.

一、觀解法的簡要介紹

觀解法立足于數(shù)軸法，它完全按照向右觀察和表達(dá)數(shù)軸的習(xí)慣，預(yù)先要求將不等號的開口方向全部統(tǒng)一向右，當(dāng)然左邊空時系負(fù)無窮大，而右邊空則正無窮大.同時此法結(jié)合在數(shù)軸上不等式組的公共解集明顯由兩邊向中間靠攏的特征，左邊部分向中間靠攏時呈向右趨勢，而在數(shù)軸上越往右越大，所以“左大”，同理右邊部分向中間靠攏時呈向左趨勢，而在數(shù)軸上越往左越小，所以“右小”，所以它的取值原則為“左大右小”.綜上可以歸納出觀解法求不等式組的基本思路為：⑴確定每一個不等式組的解集；⑵依向右觀察和表達(dá)數(shù)軸的習(xí)慣，統(tǒng)一所有不等號開口方向向右，約定左邊空負(fù)無窮大，右邊空正無窮大；⑶依“左大右小”的原則確定不等式組的解集；⑷檢查解集，若所得解集不成立，則此不等式組無解.

二、不含參數(shù)的不等式組

例1 解下列一元一次不等式組：

依“左大右小”得不等式組的解集為11＜x＜20.

問：為什么解集是 11＜x＜20，而不是 11≤x＜20 或者其他結(jié)果呢？

答：因為11≤部分能取到最小值11，而11＜部分任取一個數(shù)都大于11，所以左邊較大的是11＜；同樣地，≤20部分能取到最大值20，而＜20部分任取一個數(shù)都小于20，所以右邊較小的是＜20.

三、含有參數(shù)的不等式組

A.m≥3 B.m=3 C.m＜3 D.m≤3

將不等式組解集中不等號開口變?yōu)橄蛴矣?＜x.

現(xiàn)依“左大右小”的定值原則可得m≤3，故選D.

疑惑1：為什么是m≤3，而不是m＜3、m＞3或別的答案？

解惑 1：依“左大右小”，顯然 m＜3，因為如果 m＞3的話，解集將是m＜x，不合題意.

綜上分析，可得m≤3.

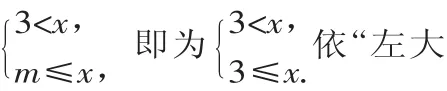
依題意不等式組有解集-1＜x＜1，現(xiàn)對照左右數(shù)值，可得

所以（a+1）（b-1）=（1+1）（-2-1）=-6.

A.6＜m＜7 B.6≤m＜7 C.6≤m≤7 D.6＜m≤7

而題意指出該不等式組有4個整數(shù)解，可以推知此4個整數(shù)解為 3、4、5、6.

為了3≤x＜m只能取到3、4、5、6這四個整數(shù)解，則有6＜m≤7，故選 D.

疑惑 2：為什么是6＜m≤7，而不能是6≤m＜7或其他情形呢？

解惑2：依題意，可以明顯推斷出6＜m＜7.接下來分析兩個端點的情形.假設(shè)m=6，此時解集為3≤x＜6，它只含三個整數(shù)解3、4、5，不合題意，故 m≠6；再假設(shè) m=7，此時解集為 3≤x＜7，它能取到四個整數(shù)解 3、4、5、6，符合題意.綜上所述，可得 6＜m≤7.

誠然，觀解法立足于數(shù)軸法，卻優(yōu)于數(shù)軸法，它簡化了求解的環(huán)節(jié)與過程，提高了速度與準(zhǔn)確度，弱化了求解難度，同時它同樣能直觀快捷地求解出含多個不等式、端點不易確定等復(fù)雜情形以及含有參數(shù)的情形.只要熟練掌握和運用此法，不等式組問題將會變得非常簡單.

1.高曉兵.“遙望”交并問題［J］.考試周刊，2011（25）：82.

2.江就好.例談用數(shù)形結(jié)合法解一類不等式組問題［J］.初中數(shù)學(xué)教與學(xué)，2011（06）：20～21.