數形結合思想在中學數學的應用
☉湖北省武漢市旭光學校 張東林
一、數形結合思想的概述
數與形是數學中兩個最古老、最基本的元素,是數學大夏深處的兩塊基石.在解決數學問題時,常常根據數學問題的條件和結論之間的內在聯系,將數的問題利用形來觀察,揭示其幾何意義;而形的問題也常借助數去思考,分析其代數含義,如此將數量關系和空間形式巧妙地結合起來,并充分利用這種“結合”,尋找解題思路,使問題得到解決的方法稱之為數形結合的思想方法.
數形結合是一個數學思想方法,包含“以形助數”和“以數輔形”兩個方面,其實質是將抽象的數學語言與直觀的圖像結合起來,關鍵是代數問題域圖形之間的相互轉化,它可以使代數問題幾何化,幾何問題代數化.下面結合具體實例談談數形結合思想在解題中的應用.
二、以形助數
幾何圖形具有直觀易懂的特點,所以在談到“數形結合”時,更多的老師和學生更偏好于“以形助數”,利用幾何圖形解決代數問題,常常會產生“出奇制勝”的效果,使人愉悅.幾何直觀運用于代數主要有以下幾個方面:
(1)利用幾何圖形幫助記憶代數公式,例如:
a)正方形的分割圖可以用來記憶完全平方公式;
b)將兩個全等的梯形拼成一個平行四邊形可以用來記憶梯形面積公式等.
(2)利用數軸或坐標系將一些代數表達式賦予幾何意義,通過構造幾何圖形,依靠直觀幫助解決代數問題,或者簡化代數運算.比如:
a)絕對值的幾何意義就是數軸上兩點之間的距離;
b)數的大小關系就是數軸上點的左右關系,可以用數軸上的線段表示實數的取值范圍;
c)互為相反數在數軸上關于原點對稱(更一般地:實數a與b在數軸上關于對稱,換句話說,數軸上實數a關于b的對稱點為2b-a).
(3)利用函數圖像的特點把握函數的性質:一次函數的斜率(傾斜程度)、截距,二次函數的對稱軸、開口、判別式、兩根之間的距離等.
(4)一元二次方程的根的幾何意義是二次函數圖像與x軸的交點.
(5)函數解析式中常數項的幾何意義是函數圖像與y軸的交點(函數在x=0時有意義).
(6)銳角三角函數的意義就是直角三角形中的線段比例.


圖1
即看做是坐標系中一動點(x,0)到兩點(0,2)和(2,1)的距離之和,于是本問題轉化為求最短距離問題.
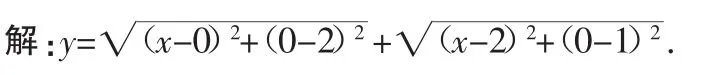
令P(x,0)、A(0,2)和B(2,1),則y=PA+PB.
作B點關于x軸的對稱點B′(2,-1),則y的最小值為AB′=
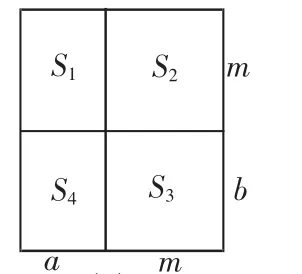
圖2
分析:本例證法雖有很多,但若用幾何圖形面積去證,則更能看清問題的實質.
證明:利用a,b,m構造矩形(如圖2).S1=ma,S3=mb,因為a 所以S1+S4 例3 已知:0 圖3 證明:如圖3,作邊長為1的正方形ABCD,在AB上取點E,使AE=a;在AD上取點G,使AG=b,過E,G分別作EF∥AD交CD于F;作GH∥AB交BC于H.設EF與GH交于點O,連 接 AO,BO,CO,DO,AC,BD.由題設及作圖知△AOG、△BOE、△COF、△DOG均為直角三角形,因此 小結:在求證條件不等式時,可根據題設條件作出對應的圖形,然后運用圖形的幾何性質或者平面幾何的定理、公理去建立不等式使結論獲證. 分析:根據正切函數的意義不難構造出滿足條件的角α、β(如圖4),怎樣構造這兩個角的和是解決這個問題的關鍵.將圖4中下面的圖翻轉到上圖的下面,就形成了如圖5的圖形,角α+β也就構成了. 證明:如圖5,連接BC,易證:△ABD≌△CBE,從而△ABC是等腰直角三角形,于是:α+β=45°. 圖4 圖5 要在解題中有效地實現“數形結合”,最好能夠明確“數”與“形”常見的結合點,從“以數助形”角度來看,主要有以下兩個結合點. (1)利用數軸、坐標系把幾何問題代數化(在高中我們還將學到用“向量”把幾何問題代數化). (2)利用面積、距離、角度等幾何量來解決幾何問題,例如:利用勾股定理證明直角、利用三角函數研究角的大小、利用線段比例證明相似等. 例5 如圖6,過正方形ABCD的頂點C任作一直線與AB、AD的延長線分別交于E、F.求證:AE+AF≥4AB. 分析:這是“形”的問題,但要直接從“形”入手很棘手.引導學生將結論變為 圖6 從此式形式上看,聯想起一元二次方程根的判別式,從而把“形”的問題轉化成“數”的問題來解決. 證明:設AB=a,AE=m,AF=n.連接AC,則 所以mn=a(m+n).設m+n=p,mn=ap.所以m,n是方程x2-px+ap=0的兩根,而m,n為實數,故△=p2-4ap≥0,又p>0,所以p≥4a,即AE+AF≥4AB. 例6 如圖7,在正△ABC的三邊AB,BC,CA上分別有點D,E,F.若DE⊥BC,EF⊥AC,FD⊥AB同時成立,求點D在AB上的位置. 分析:先假設符合條件的點D,E,F已經作出,再利用已知條件,尋找線段與角之間的數量關系,列出含有待求量的等式(方程),以求其解. 解:設AB=1,AD=x. 因為△ABC為正三角形,且DE⊥BC,EF⊥AC,FD⊥AB, 故 AF=2x,CF=1-2x,CD=2CF=2-4x,BE=1-CE=4x-1,BD=2BE=8x-2. 而AD+BD=1,即x+(8x-2)=1. 小結:幾何中存在著這樣一類問題,即幾何圖形中的某些點的位置或線段的長度或角度的大小不能依題意畫出來,只有根據已知條件求出某一些量時,圖形才能畫出.而求那些量的方法,常常是通過列方程(組),即轉化為代數方程求解. 總之,數形結合思想是數學中基本而又重要的思想,是解決數學試題的一種常用方法與技巧,特別是在解決選擇、填空題中發揮著奇特功效.數學家華羅庚曾指出:“數缺形時少直觀,形少數時難入微;數形結合百般好,隔裂分家萬事非.”可見數形結合的思想可以使某些抽象的數學問題直觀化、生動化,能夠變抽象思維為形象思維,有助于把握數學問題中的本質.在中考復習時,同學們必須隨時注意運用數形結合思想,復習中要以熟練技能、方法為目標,加強這方面的訓練,以提高解題能力和速度. 1.程曠主.巧學初中數學80法.農村讀物出版社 2.九年義務教育初中數學課本.北京:人民教育出版社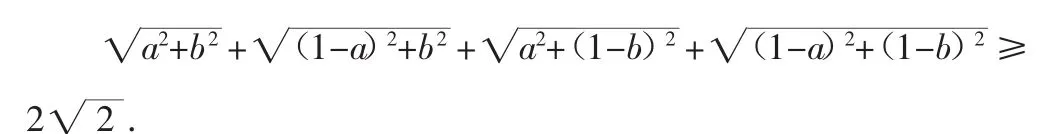


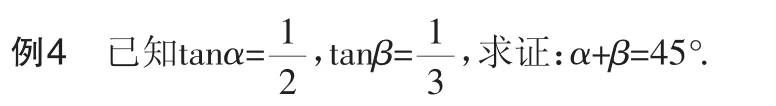
三、以數解形