解析初中數學中分式方程的解法及應用

☉江蘇省揚州市江都區實驗初級中學 姚永華

解析初中數學中分式方程的解法及應用

☉江蘇省揚州市江都區實驗初級中學 姚永華

分式方程的解法及應用是中考考查的重點內容，考查時大多以直接解分式方程和列分式方程解應用題的形式出現.因此，對本部分知識需要進行專項訓練，熟練掌握解分式方程的方法，并通過應用題使學生進一步使用代數中的方程去反映現實世界中的等量關系，體會代數方法的優越性，進一步培養學生化實際問題為數學問題的能力和分析問題解決問題的能力.下面就對分式方程的解法及其應用做具體解析.

一、分式方程的有關概念

分式方程是方程中的一種，且分母里含有未知數的（有理）方程叫做分式方程.

二、分式方程的解法

解分式方程的基本思路是將分式方程化為整式方程，具體做法是“去分母”，即方程兩邊同乘最簡公分母，這也是解分式方程的一般思路和做法.

1.去分母

方程兩邊同時乘以最簡公分母（最簡公分母：①系數取最小公倍數②出現的字母取最高次冪③出現的因式取最高次冪），將分式方程化為整式方程；若遇到互為相反數時.不要忘了改變符號.

2.解整式方程

移項，若有括號應去括號，注意變號，合并同類項，把系數化為1求出未知數的值；

3.驗根

求出未知數的值后必須驗根，因為在把分式方程化為整式方程的過程中，擴大了未知數的取值范圍，可能產生增根.驗根時把整式方程的根代入最簡公分母，如果最簡公分母等于0，這個根就是增根.否則這個根就是原分式方程的根.若解出的根是增根，則原方程無解.如果分式本身約分了，也要帶進去檢驗.一般的，解分式方程時，去分母后所得整式方程的解有可能使原方程中分母為零，因此要將整式方程的解代入最簡公分母，如果最簡公分母的值不為零，則是方程的解.

（1）注意去分母時，不要漏乘整式項.（2）増根是分式方程去分母后化成的整式方程的根，但不是原分式方程的解.（3）増根使最簡分母等于0.

三、分式方程的應用

列分式方程解應用題的一般步驟是：找等量關系—設—列—解—檢驗—答.

例1 玉樹地震后，有一段公路急需搶修，此項工程原計劃由甲工程隊獨立完成，需要20天，在甲工程隊施工4天后，為了加快工程進度，又調來乙工程隊與甲工程隊共同施工，結果比原計劃提前10天，為抗震救災贏得了寶貴時間，求乙工程隊獨立完成這項工程需要多少天？

考點：分式方程的應用．專題：工程問題．分析：等量關系為：甲工作量+乙工作量=1．

解析：設乙工程隊獨立完成這項工程需要x天．

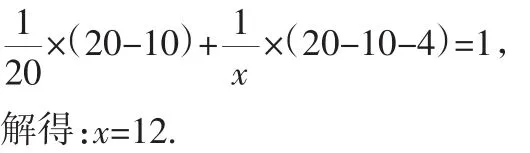
經檢驗x=12是原方程的解．

答：乙工程隊獨立完成這項工程需要12天．

點評：工作量問題常用的等量關系為：工作量之和為1，易錯點是準確找到各個隊的工作時間．

例2 某公司開發生產的1200件新產品需要精加工后才能投放市場，現有甲、乙兩個工廠都想加工這批產品．公司派出相關人員分別到這兩間工廠了解生產情況，獲得如下信息：

信息一：甲工廠單獨加工完成這批產品比乙工廠單獨加工完成這批產品多用10天；

信息二：乙工廠每天比甲工廠多加工20件．

根據以上信息，求甲、乙兩個工廠每天分別能加工多少件新產品.

考點：分式方程的應用．

分析：總工作量除以所用時間即為工效，而乙工廠每天比甲工廠多加工20件的前提下，甲工廠單獨完成比乙工廠單獨完成多用10天，據此可列方程．

解：設甲工廠每天能加工x件新產品，則乙工廠每天能加工（x+20）件新產品．

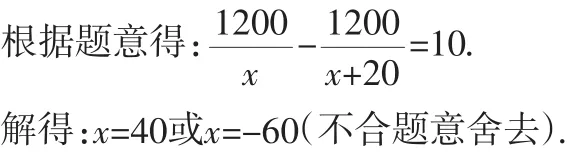
經檢驗：x=40是所列方程的解．

乙工廠每天加工零件為：x+20=60．

答：甲工廠每天能加工40件新產品，乙工廠每天能加工60件新產品．

點評：理解題意找出題中的等量關系，列出方程，注意分式方程一定要驗根．

例3 在某道路拓寬改造工程中，一工程隊承擔了24千米的任務.為了減少施工帶來的影響，在確保工程質量的前提下，實際施工速度是原計劃的1.2倍，結果提前20天完成了任務，求原計劃平均每天改造道路多少千米.

解析：該題目的等量關系是計劃用的天數-實際用的天數=20天

設原計劃平均每天改造道路x千米，根據題意，得：

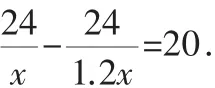
解這個方程，得x=0.2.

經檢驗，x=0.2是原方程的解.

答：原計劃平均每天改造道路0.2千米.

例4 杭州國際動漫節開幕前，某動漫公司預測某種動漫玩具能夠暢銷，就用32 000元購進了一批這種玩具，上市后很快脫銷，動漫公司又用68 000元購進第二批這種玩具，所購數量是第一批購進數量的2倍，但每套進價多了10元.求：

（1）該動漫公司兩次共購進這種玩具多少套？

（2）如果這兩批玩具每套的售價相同，且全部售完后總利潤率不低于20%，那么每套售價至少是多少元？

解：（1）設動漫公司第一次購進x套玩具，由題意得：

經檢驗，x=200是所列方程的根.

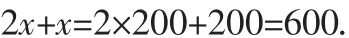
所以動漫公司兩次共購進這種玩具600套.

（2）設每套玩具的售價為y元，由題意得：

解分式方程作為基礎性知識，在中考中以直接考查為主，也經常與數軸等知識綜合考查，解決問題時要注意分式方程根的檢驗是必不可少的步驟.列分式方程解應用題，在中考中多以解答題為主，有時也會出現在選擇題或填空題中，解決此類題目的關鍵是準確理解題意，確定題目中的等量關系，列出分式方程.而在解此時的分式方程時，不僅要檢驗所得解的是否滿足方程式，還要檢驗是否符合題意.