初中數(shù)學(xué)對稱性解題方法探討
☉廣東省深圳市南山區(qū)桃源中學(xué) 譚煒東
1.引言
20世紀(jì)德國著名數(shù)學(xué)家赫爾曼·外爾說過:“對稱是一個廣闊的主題,在藝術(shù)和自然兩方面都意義重大,數(shù)學(xué)則是它的根本.”初中數(shù)學(xué)題目中有不同類型的對稱,像代數(shù)中,有對稱多項式、對稱方程式、對稱恒等式、對稱不等式等;而幾何中,有等腰三角形、正方形、平行四邊形、圓柱、球等軸對稱圖形和中心對稱圖形.不僅如此,在一些數(shù)學(xué)問題中還會潛在涉及到對稱,像數(shù)學(xué)題目中往往存在關(guān)系、邏輯、位置等的對稱.在分析、解決與對稱相關(guān)的數(shù)學(xué)題時,就可以運用對稱思想來解題,不僅可以避免思路、步驟的煩瑣,使解題又快又簡,還能發(fā)散學(xué)生的思維,提高學(xué)生的動腦能力.
2.對稱思想
數(shù)學(xué)中的對稱法,就是依據(jù)對稱原理,應(yīng)用抽象或者形象思維,建立具有對稱特點的數(shù)學(xué)模型、幾何圖形或者代數(shù)表達(dá)式,在代數(shù)和幾何解題中發(fā)揮著重要的作用.古希臘的雕塑家波利克里托斯在公元前五世紀(jì)最早提出了對稱這個名詞,后來畢達(dá)哥拉斯、弗賴、赫爾曼·外爾、徐一鴻等都從不同角度給出了各自的解釋.
數(shù)學(xué)中的對稱一般是指代數(shù)對稱和幾何對稱.偉大的數(shù)學(xué)家泰勒斯在公元前就提出了“圓的直徑將其平分”、“等腰三角形的兩個底角相等”等,這在我們目前的初中數(shù)學(xué)中已經(jīng)是作為定理來使用的,但是在公元前泰勒斯就意識到這種對稱的思想,并且用論證的方法證明這些命題的正確性.我國的張奠宙教授就從對稱的視角出發(fā),列舉了中學(xué)數(shù)學(xué)中關(guān)于對稱的例子,像(a+b)n=a·n+b·n,a+b=b+a等.
3.對稱法在初中數(shù)學(xué)解題中的應(yīng)用
目前,在代數(shù)和幾何的解題過程中,都運用了大量的對稱思想.下面就初中數(shù)學(xué)中比較典型的對稱問題進(jìn)行解釋分析,探討如何在代數(shù)和幾何解題中運用對稱思想的.
3.1 對稱法在代數(shù)中的應(yīng)用
(1)運用對稱求最值
例1 已知a>0,b>0,且z=ab,則當(dāng)a+b=2時,求z的最大值.
分析:首先尋找解題的關(guān)鍵點.本題中的關(guān)鍵就是條件a+b=2,a與b的和是一個定值,那么就會想到當(dāng)a大時,b就小;b大時,a就小;或者a、b是相等的,即a、b在關(guān)系上是對稱的.其次,尋找到解題點后,就開始思考如何能恰當(dāng)?shù)乩胊、b的對稱來解題.因為a、b的和是2,那么讓a=1-r,則b=1+r,這樣就能合理應(yīng)用a、b的對稱性.最后,z=ab=(1-r)(1+r)=1-r2,而r2是永遠(yuǎn)大于等于零的,所以只有r=0的時候,z的值最大,z=1.
解:設(shè)a=1-r,b=1+r,所以z=ab=(1-r)(1+r)=1-r2.
而r2≥0,所以z=1-0=1,可知z的最大值是1.
(2)運用對稱證明不等式
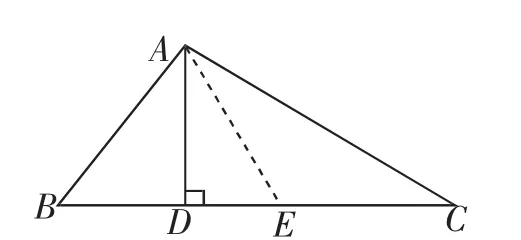
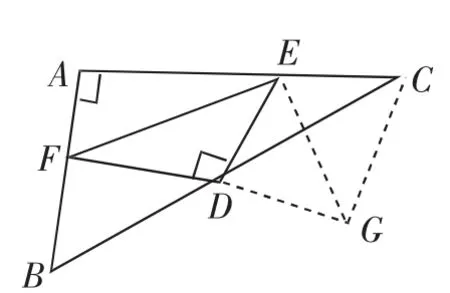
例2 已知0 分析:通過觀察,發(fā)現(xiàn)這個式子有對稱存在,所以要證明整個不等式成立,只需要證明或者即只需要證明其中一個式子成立即可.接下來考慮怎么創(chuàng)設(shè)條件,證明成立. 圖1 (1)運用對稱證明兩個角之間的關(guān)系 例3 如圖1,AD是銳角三角形ABC的高,其中AB+BD=CD,求證∠B=2∠C. 分析:這個證明題中,只有AB+BD=CD和AD是高這兩個條件,那么可以思考是否能根據(jù)對稱創(chuàng)設(shè)另一個關(guān)于線段的關(guān)系,可以相互替代,從而證明角之間的關(guān)系,并且∠B和∠C也能聯(lián)系起來.因此,可以考慮做AB關(guān)于高AD的對稱線AE,創(chuàng)建一個軸對稱圖形,那么AB=AE,則可以知道AE+BD=CD.又因為軸對稱,所以BD=DE,因此,AE+DE=CD,所以AE=EC,進(jìn)而得出∠EAC=∠C,∠AEB=2∠C.最終∠B=2∠C的結(jié)論就可以成立了. 圖2 (2)運用對稱求代數(shù)幾何相結(jié)合的問題 例4 如圖2,在△ABC中∠A=90°,點D為BC中點,點E、F分別在AC、AB上,且∠EDF=90°,試說明:BF2+CE2=EF2. 分析:要求證明三角形中邊的關(guān)系,并且三條邊不在一個三角形中,因此,考慮如何創(chuàng)設(shè)一個三角形,并且利用邊角的關(guān)系來證明.如圖2,延長FD,作FD=DG,又因為BD=CD,可以發(fā)現(xiàn)三角形BDF和三角形CDG全等,所以GE=EF,BF=CG,進(jìn)而再通過直角三角形中角的關(guān)系,證明ECG是個直角三角形,最終就可以證明結(jié)論的成立. 綜上所述,在數(shù)學(xué)解題過程中如果合理的使用對稱法,不僅可以使問題得到簡化,還能發(fā)散學(xué)生的思維,提高學(xué)生的創(chuàng)造力.因此,教師在平時的教學(xué)中,要重視和提高學(xué)生對稱性思維解題的能力.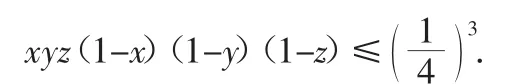

3.2 對稱法在幾何中的應(yīng)用
4.結(jié)論

