基于學生視角的“用形解數”教學

☉浙江省余姚市第四中學 魯建橋

調查發現，“用形解數”因為可以直觀、迅捷地解決某些代數問題，而深受學生的喜歡.但是，喜歡并不等于容易掌握，很多學生認為“用形解數”這種方法技巧性過強、不容易想到，而且一不小心就會犯錯.基于學生對“用形解數”這種方法的認識，筆者認為，在教學過程中應從學生的困惑入手，關注以下兩方面的問題.

一、“數”中思“形”，活用“基本幾何模型”

在高中階段的學習過程中，因為解析幾何學科的開設，“用數解形”相對于“用形解數”使用更為普遍.然而，解析幾何中的一些公式與方程，例如，直線斜率直線截距ax+by、距離公點到直線，還有向量的模長與夾角公式等等都可以作為溝通數形間關系的橋梁，實現“數”向“形”的轉化，在這里我們將它們稱為“基本幾何模型”.學生如果熟練掌握這些“基本幾何模型”，不僅可以豐富代數式的幾何意義，而且可以利用“基本幾何模型”解決一些相對復雜的代數問題.

例1 求證：（a1b1+a2b2）2≤（a12+a22）（b12+b22）.

上述問題的證明并不困難，但我們可以利用“基本幾何模型”，豐富代數式的幾何意義.

上述問題若用代數方法求解，計算較煩，花時較多.但如果充分利用“基本幾何模型”，將表達式適當變形，將問題轉化，我們可以挖掘代數式的幾何意義，簡化求解過程.

在平時的教學過程中，我們應幫助學生掌握“基本幾何模型”，引導學生將復雜代數式進行化歸，從不同角度挖掘代數式所具有的幾何意義，體現數學問題解決的一般過程.同時，在教學過程中，老師也應向學生暴露思維過程，揭開“用數解形”的神秘面紗.

二、“形”來助“數”，把握教學契機

A.1 B.2 C.3 D.4

上述問題“用形解數”并不是最明智的選擇，但是因為是解的個數問題，學生比較容易想到作出函數y=f（x）和函數y=x的圖像判斷交點個數，易錯選B.究其原因，作草圖不好判斷拋物線與斜直線（不垂直于坐標軸的直線）的交點個數.這個時候，老師不應否定學生的做法，而是引導學生將問題轉化為f（x）-x=0，從而考查函數y=f（x）-x和x軸的交點個數問題，學生容易作出正確的選擇，答案為C.

例4 已知方程2x-1+2x2-a=0有兩根，則a的范圍是______.

此題出現在近期高三復習資料中，設計者的意圖是強化函數與方程的聯系，突出數形結合這一重要思想.

面對上述問題，學生容易形成共識：（1）此方程不能用常法判斷；（2）可以轉化為函數f（x）=2x-1和g（x）=-2x2+a的圖像的交點個數判斷.因此作出相應的圖像（如圖1），得到結論.這樣的結果跟資料提供的答案一樣，但事實上是不正確的.

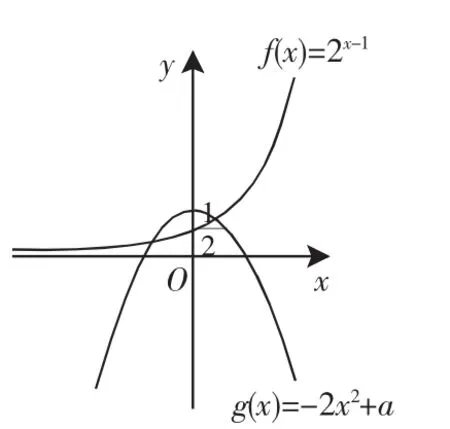
圖1

這個時候，我們面對的是一個沒有確切答案的問題，但卻是幫助學生正確掌握“用形解數”這種方法的一個契機.我們不妨引導學生進行思考、質疑：函數f（x）=2x-1的圖像和函數g（x）=-2x2+a的圖像真的像我們所作的圖1那樣嗎？它們會不會相切于某一點呢？

事實上，兩函數圖像會相切于一點，記為P.那么過P點存在兩函數圖像的公切線l（如圖2）.利用這條切線的斜率可以建立關于x0的方程，從而只需求解x0即可.

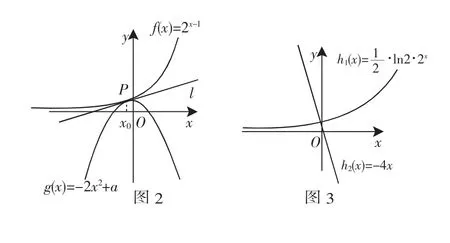
簡解如下：設點P的坐標為（x0，y0），則有注意到此方程不能直接求解，則再作出函數和的草圖（如圖3）.我們不難發現兩函數圖像在第二象限有交點，即存在x0<0滿足方程那么a的范圍應該是a>2x02-4x0.

我想通過這個問題的質疑與探究，學生肯定能夠進一步認識到：畫出函數圖像的確能使問題變得直觀具體，但是我們只有借助對“數”的精確分析才能準確地刻畫“形”的細微變化，從而更好地掌握“用形解數”這種方法.

我們不難發現：很多學生在運用“用形解數”這種方法解決代數問題的過程中，經常表現出用隨意性的草圖來刻畫代數問題，從而導致最后不能準確地解決相關問題.這個現象提醒我們在我們平時的課堂教學應特別注意這一問題.比如在作正弦函數y=sin x和正切函數y=tan x的圖像時，能夠借助直線y=x來畫，體現當時三者所具有的關系：sin x

既然“用形解數”是學生喜歡的數學方法，既然學生在運用這種方法的時候還有困惑與困難，那我們就應該從學生的視角去理解他們所面臨的問題，開展針對性的教學，只有這樣，才能幫助學生做到從“喜歡”到“掌握”，才能讓“形”為“數”插上輕盈的翅膀.