導數在解決函數問題中的應用

☉浙江省上虞市上虞職教中心 陳 軼

導數是解決函數的單調性、極值、最值、切線等問題的有力工具，作為高中數學的新增內容之一，運用導數研究函數的恒成立、最值、方程、不等式的證明等問題是近幾年高考的熱點，也將是命題的新增長點.如果給定函數解析式次數高于二次、形式復雜時，常考慮用導數解決函數問題.

一、利用導數解決函數單調性問題

當函數的表達形式復雜、用初等函數不能求解時，常考慮用導數的方法求解.通常先由導數公式求出f′（x），解關于f′（x）的不等式時注意分類討論的思想.

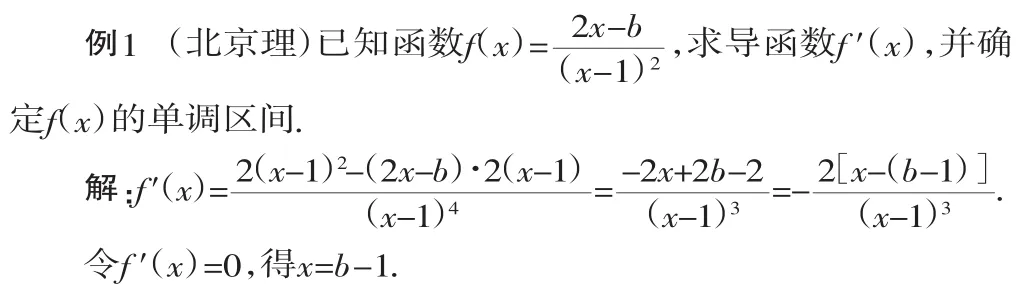
當b-1<1，即b<2時，f′（x）的變化情況如下表：

x （-∞，b-1） b-1 （b-1，1） （1，+∞）f′（x）-0+-

當b-1>1，即b>2時，f′（x）的變化情況如下表：

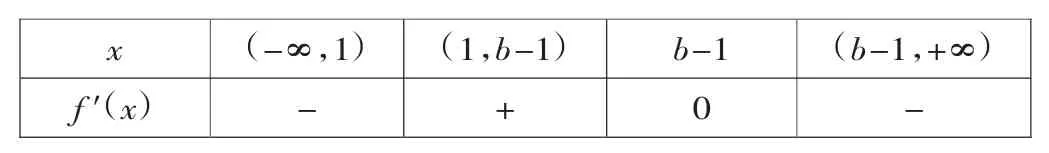
x （-∞，1） （1，b-1） b-1 （b-1，+∞）f′（x）-+0-

當b<2時，函數f（x）在（-∞，b-1）、（1，+∞）上單調遞減，在（b-1，1）上單調遞增；

當b>2時，函數f（x）在（-∞，1）、（b-1，+∞）上單調遞減，在（1，b-1）上單調遞增；

點評：求導后的分類討論問題應注意：一要找分類點（根的大小比較、含x的最高次項系數正負的確定）、列表；二要結合代數方法（如分解因式、配方法、解方程或不等式，處理導函數的正負問題.

二、利用導數解決函數的最值問題

對閉區間的可導函數求其最值時，先求出函數的極值，再比較端點值的函數值與極值的大小，從而確定出函數的最大值、最小值.

（1）求函數f（x）的單調區間.

（2）設g（a）為f（x）在區間［0，2］上的最小值.

（i）寫出g（a）的表達式；

（ii）求a的取值范圍，使得-6≤g（a）≤-2.

若a≤0，則f′（x）>0，f（x）的單調遞增區間是［0，+∞）.

點評：本題主要考查函數的性質、求導、導數的應用等基礎知識，同時考查分類討論思想.立足基礎，解決問題，突出導數的工具性.

三、利用導數解決函數的恒成立問題

恒成立問題是近幾年的熱點，一般有兩種典型結構：“a≤f（x）恒成立”、“a≥f（x）恒成立”.解決的方法是求f（x）的最小值m或最大值M，將問題轉化為“a≤m”或“a≥M”.尤其要注意端點值的取舍問題.

設g（x）=2（1+x）ln（1+x）-x2-2x，則g′（x）=2ln（1+x）-2x.

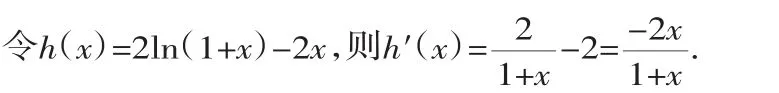
當-10，h（x）在（-1，0）上為增函數.

當x>0時，h′（x）<0，h（x）在（0，+∞）上為減函數.

所以h（x）在x=0處取得極大值.h（0）=0.

所以g′（x）<0（x≠0），函數g（x）在（-1，+∞）上為減函數.

于是當-1g（0）=0，當x>0時，g（x）

所以，當-10，f（x）在（-1，0）上為增函數.

當x>0時，f′（x）<0，f（x）在（0，+∞）上為減函數.

故函數f（x）的單調遞增區間為（-1，0），單調遞減區間為（0，+∞）.

點評：本題尋找恒成立的方法是通過兩邊取對數化指數問題為對數函數問題，分離參數轉化為“a≤f（x）恒成立”的類型，利用第一問中結論證明G′（x）≤0恒成立，進而借助函數單調性尋找其最小值大于a成立，手法新穎，突破了常規 .

四、利用導數解決切線方程問題

利用導數求曲線的切線方程，關鍵是求出切線的切點和斜率，方法是設出切點坐標，由導數公式求出切線斜率.

例4 （湖北文）已知函數f（x）=x3+mx2-m2x+1（m為常數，且m>0）有極大值9.

（1）求m的值；

（2）若斜率為-5的直線是曲線y=f（x）的切線，求此直線方程.

解：（1）由f′（x）=3x2+2mx-m2=（x+m）（3x-m）=0，得：x=-m或

當x變化時，f′（x）與f（x）的變化情況如下表：

x （-∞，-m） -m -m，1 3（ ）m 1 3m 1 3m，+∞（ ）f′（x）+0-0+f（x）↗極大值↘極小值↗

從而可知，當x=-m時，函數f（x）取得極大值9.

即f（-m）=-m3+m3+m3+1=9.解得m=2.

（2）由（1）知，f（x）=x3+2x2-4x+1，依題意知f′（x）=3x2+4x-4=-5.

即5x+y-1=0或135x+27y-23=0.

點評：利用導數求曲線的切線方程幾乎是每年高考必考的內容，關鍵是利用導數求出切線的斜率，確定切點坐標.

總之，利用導數研究函數的單調性、最值、恒成立、方程等問題 ，充分論證了導數的工具作用.導數把圖形中的信息表達為代數信息，實現了數與形的和諧統一，使問題的解決更加簡單清晰.