構造直角三角形巧解一類三角求值問題

☉江西省全南中學 肖秋蓮

已知角的某種三角函數值，求其他三角函數值的問題，是學生學習中的一個難點.同學們在求解這類問題時，往往由于解題方法的選擇不當而一籌莫展.筆者多年的教學實踐表明，在處理一些三角求值問題時，若能充分利用三角問題中所具有的圖形特征，通過構造直角三角形，利用直角三角形的邊角關系，便可簡潔、迅速地使問題得到解決.下面筆者略舉數例并加以分析，供同學們學習參考.

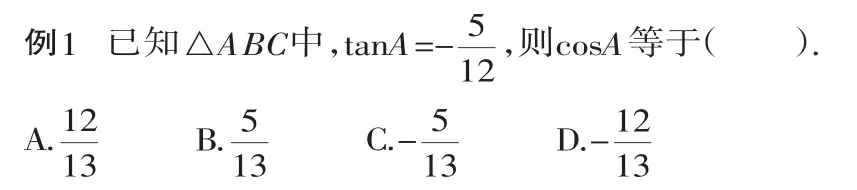
分析：已知正切值求解正、余弦，在同角三角函數的基本關系式中，并沒有現成的公式可以套用，而必須經過一系列的變形，運算量較大.本題若利用構造直角三角形，利用直角三角形的邊角關系進行求解，運算量將大大減小.下面提供兩種求解方法，來加以比較.

解法1：常規法.

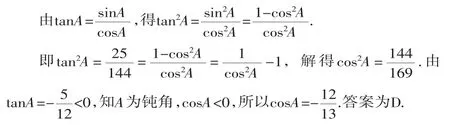
解法2：構造法.

將A看成是銳角，構造直角三角形ABC（如圖1）.

圖1

由已知tanA<0，知A是鈍角.

點評：本題若用常規方法求解，必須利用同角三角函數關系式中的平方關系和倒數關系去進行變形轉化，運算量較大.本題若用構造直角三角形法進行求解，可簡捷、快速地求得結果.

從上題的解法2中不難看出，當我們求解角的三角函數值問題時，無論這個角是不是銳角，我們都視之為銳角，先求出角的三角函數的絕對值，進而由角所在的象限，判斷出函數值的符號，從而求得待求的三角函數值，本過程可簡記為“將任意角視為銳角，絕對值不變，符號看象限”.

例2 （北師大版必修4課本第116頁例3）已知tanα=m（m≠0），求sinα和cosα的值.

分析：本題中不僅含字母參數，解題時要分情況進行討論，而且由正切轉化為正弦、余弦的過程中，公式變形也較復雜.本題若采用構造法解題，可迅速、快捷地得出正確結果，下面給出兩種解法，進行對比.

解法1：常規法（教材中提供的解法）.

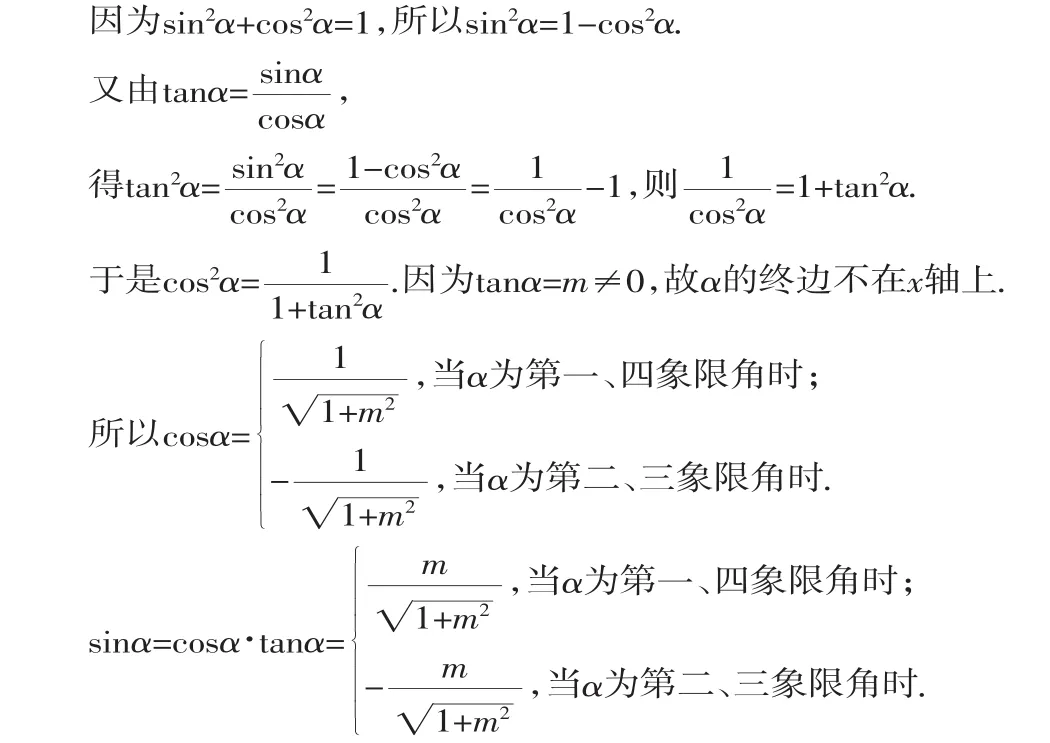
解法2：構造法.

將α看成是銳角A，構造直角三角形ABC（如圖2）.

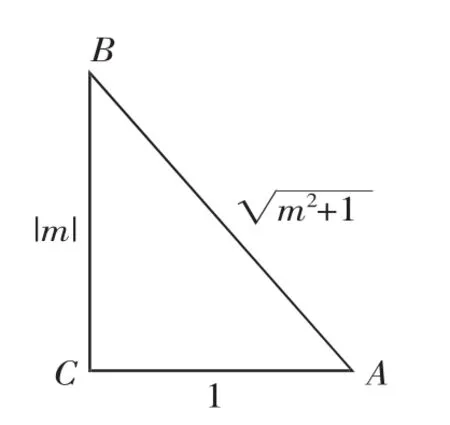
圖2

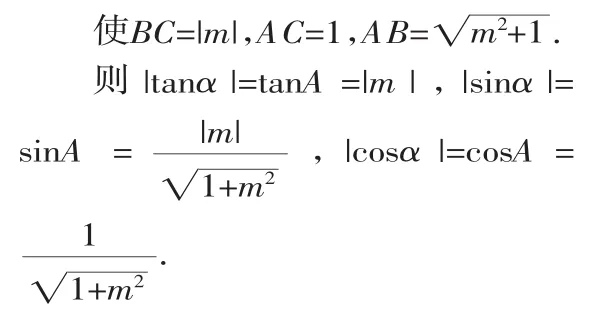
因為tanα=m≠0，α得終邊不在x軸上.

點評：解法2顯然比解法1簡單得多；因此在處理含字母的求值問題時，我們仍然可構造直角三角形，利用直角三角形的邊角關系得出函數值的絕對值，然后分情況進行討論.在討論過程中，一定要注意角的象限和字母表示的數的正負，避免因符號而導致錯解.

分析：本題是一道常規的三角求值題，利用同角三角函數的基本關系式，便可以較快求得結果.本題若用構造法進行求解，也可收到意想不到的效果.

點評：利用構造直角三角形法解題時，正確判斷三角函數值符號是解題的關鍵.

從上述數例可以看出，利用構造直角三角形求解三角函數值，既準確又快捷，尤其是在解決客觀性問題時，能起到事半功倍的效果，同學們在學習中不妨一試.