曲線積分第二中值定理“中間點”漸近性分析

林冬翠

(廣西幼兒師范高等專科學校，廣西南寧530022)

曲線積分第二中值定理“中間點”漸近性分析

林冬翠

(廣西幼兒師范高等專科學校，廣西南寧530022)

通過研究第一型曲線積分第二中值定理“中間點”的漸近性，將結論推廣到積分第二中值定理“中間點”的漸近性。首先給出第一型曲線積分第二中值定理及其證明，得出一個結論，由這個結論推導出定積分第二中值定理相應的結果。所得結論推廣了文獻［1－3］中關于積分第二中值定理的結論。

第一型曲線積分;中值定理;中間點;漸近性

0 引言

關于定積分中值定理“中間點”漸近性研究的文獻和結果有很多，并且取得了不少的成果。文獻［4］研究了在連續區間上一元函數的積分中值定理。文獻［5］研究了積分第一中值定理中間點當區間長度趨向于零時的漸近性，得出的結論對在某點不可微的函數仍然有效。文獻［1］研究了當函數f(x)在區間上連續且存在(n－1)階導數，函數g(x)在區間上存在m階導數時，積分第二中值定理“中間點”的漸近性，并且得到一系列相關的推論。文獻［2］研究了函數g(x)在區間［α，β］上連續且不變號，g(α)≠0，f(x)在區間［α，β］上單調連續，在α點處可微且f'(α)≠0時，積分第二中值定理中間點的漸近性。還研究了函數g(x)在區間［α，β］上連續且不變號，g(α)≠0，f(x)在區間［α，β］上單調連續，且存在n階導數時，積分第二中值定理“中間點”的漸近性。文獻［5］研究了函數g(x)在區間［α，β］上連續且不變號，g(α)≠0，f(x)在區間［α，β］上單調連續，且滿足=A≠0，λ＞0和A是兩個常數時，積分第二中值定理“中間點”的漸近性。文獻［6］則是在文獻［1－3］的基礎上，歸納分析關于積分第一中值定理“中間點”的漸近性的一些結果，再進而推出與之對應的關于積分第二中值定理的結果。文獻［6］中的結論分別是文獻［1－3］的結論的推廣。

然而，對于曲線積分中值定理“中間點”漸近性的研究比較少。文獻［7］利用極限理論對第一型曲線積分中值定理“中間點”的漸近性進行了探討，主要研究函數f(x，y)在光滑曲線上連續，在某點處存在一階導數且不為零時曲線積分第一中值定理“中間點”的漸近性，所得到的結論是積分第一中值定理“中間點”的漸近性的相應推廣。文獻［8－9］研究了函數f(x，y)在光滑曲線上連續，在某點處存在n階連續導數且在某點前(n－1)階導數為零，n階導數不為零時，曲線積分第一中值定理“中間點”的漸近性，所得的結論是積分第一中值定理“中間點”的漸近性的相應推廣。文獻［10］研究了函數f(x，y)在光滑曲線上連續，且滿足給定條件下的曲線積分第一中值定理“中間點”的漸近性，得到的結論是文獻［7－9］的結論的推廣，其結論也是積分第一中值定理“中間點”的漸近性相應的推廣。本文在文獻［7－10］的基礎上，討論第一型曲線積分第二中值定理“中間點”的漸近性，推廣了積分第二中值定理“中間點”的漸近性，得到的結論是文獻［1－3］的結論的推廣，其結論也是積分第二中值定理“中間點”的漸近性相應的推廣。

1 預備知識

本節主要介紹本文用到的主要引理。

引理1［4］(積分第一中值定理)若f在［a，b］上連續，則至少存在一點ζ∈［a，b］，使得

引理2［4］(推廣的積分第一中值定理)若f(x)與g(x)都在［a，b］上連續，且g(x)在［a，b］上不變號，則至少存在一點ζ∈［a，b］，使得

引理3［4］(推廣的積分第二中值定理)設函數f在［a，b］上可積，若g為單調函數，則存在ζ∈［a，b］，使得

引理4［4］如果函數f(x，y)在光滑曲線C(A，B)上連續，則存在一點M(x0，y0)∈C(A，B)，使得，其中s表示曲線C(A，B)的長。

引理5［5］若函數f(x，y)在光滑曲線C(A，B)上連續，則存在一點M(x0，y0)∈C(A，B)(端點A，B除外)，使得，其中s表示曲線C(A，B)的長。

引理6［4］如果曲線C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函數f(x，y)在曲線C(A，B)上連續，那么第一型曲線積分存在，且

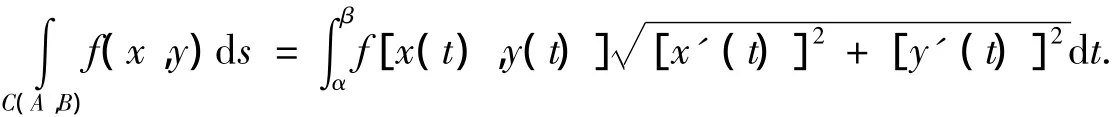
2 曲線積分第二中值定理中間點的漸近性

首先我們給出第一型曲線積分第二中值定理的證明。

定理1設函數g(x，y)在光滑曲線C(A，B):x=x(t)，y=y(t)(α≤t≤β)上可積.若f(x，y)是曲線C(A，B)上的單調函數，則存在一點M［x(ζ)，y(ζ)］∈C(A，B)(端點A，B除外)，使得

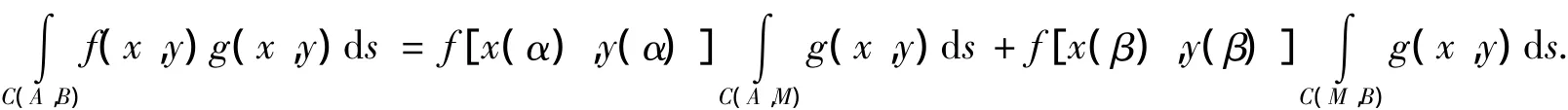
證明:由引理6得

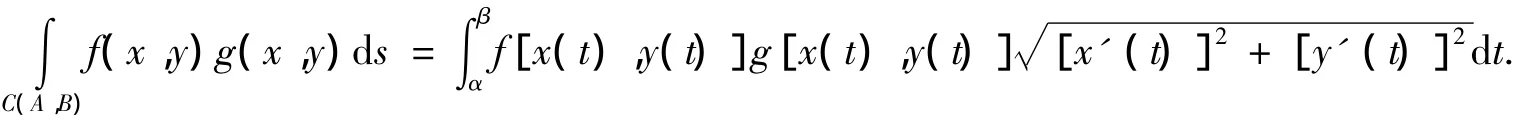
由引理3得

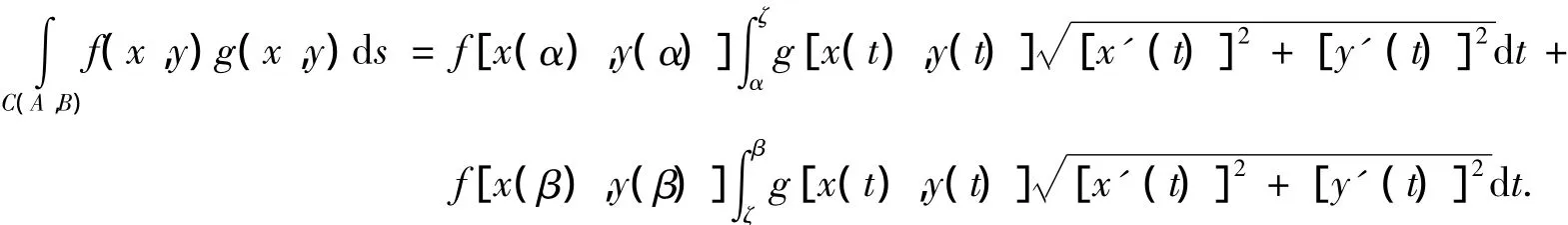
再由引理6得

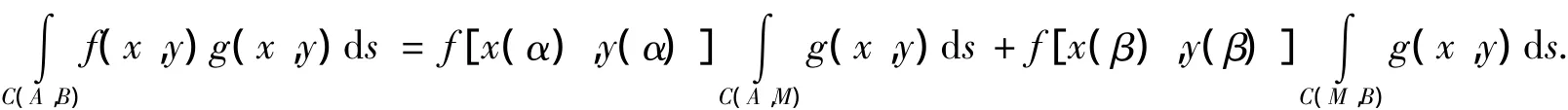
定理1獲證。

關于曲線積分第二中值定理“中間點”的漸近性，我們可得到以下幾個結論。

定理2如果曲線C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函數g(x，y)在曲線C(A，B)上連續，f(x，y)是曲線C(A，B)上關于參數t單調的函數，并且有實數q＞0，，實數p＞－1，這里h(t)=f［x(t)，y(t)］，k(t)=g［x(t)，y(t)］，A，B是兩個常數，那么定理1中的中間點M［x(ζ)，y(ζ)］∈C(A，B)有漸近性，其中s*，s分別是曲線C(A，M)和C(A，B)的長。

證明:設“中間點”M［x(ζ)，y(ζ)］對應參數t=ζ，即x0=x(ζ)，y0=y(ζ)，則有α＜ζ＜β.由引理6得到

構造輔助函數

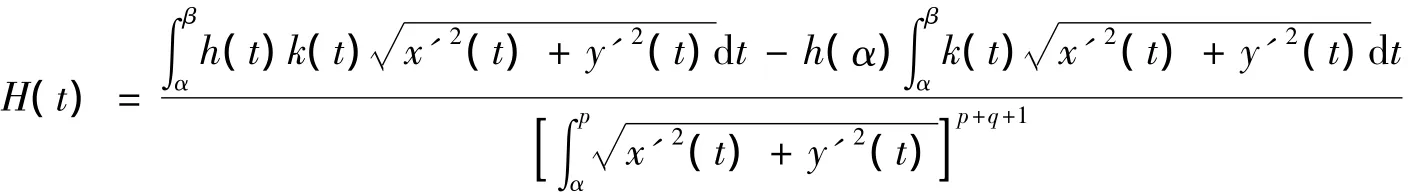
利用L’Hospital法則，我們可得到

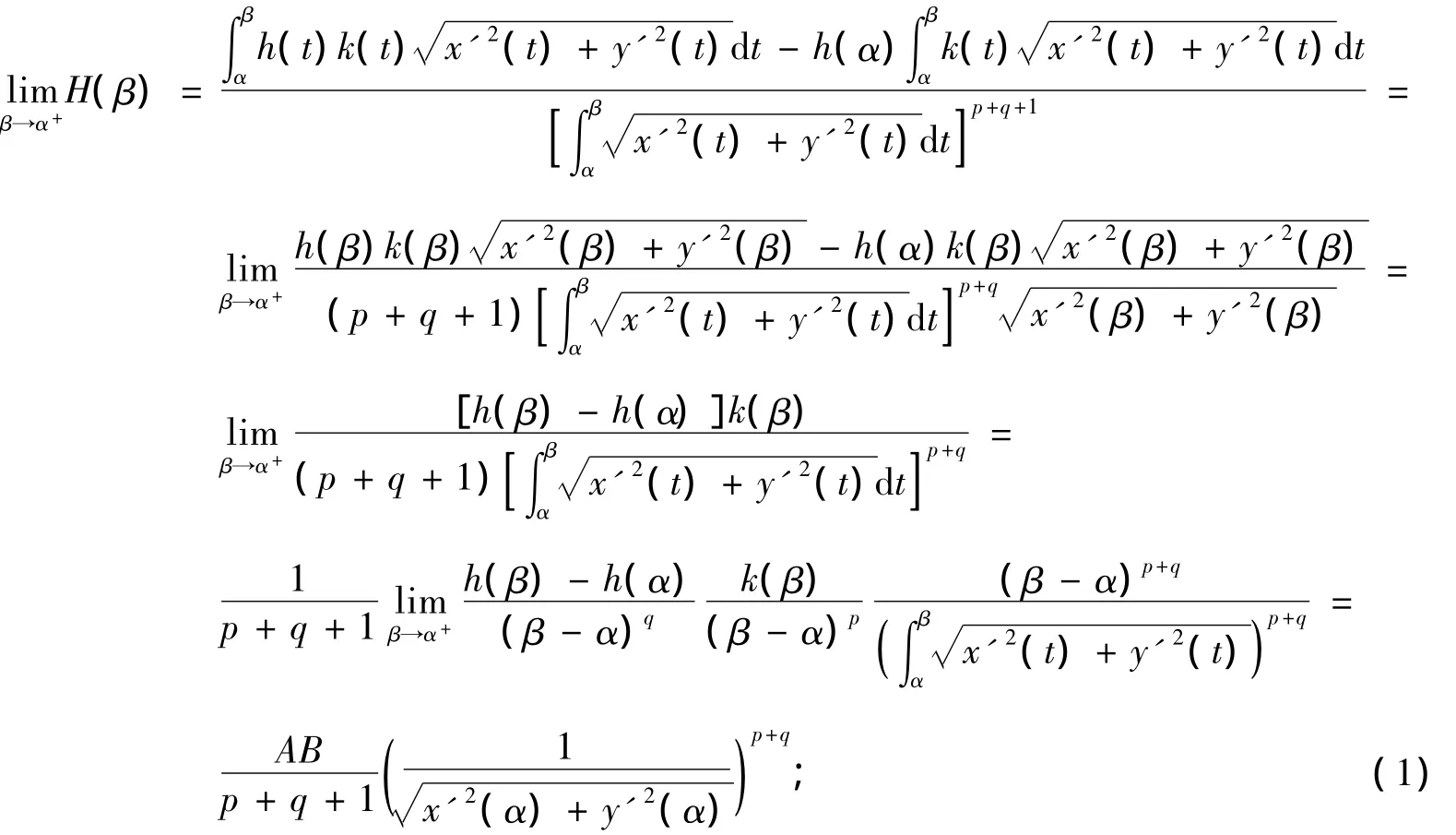
利用第一型曲線積分第二中值定理和L`Hospital法則，又得到

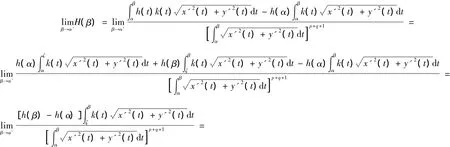
比較(1)式和(2)式，我們有

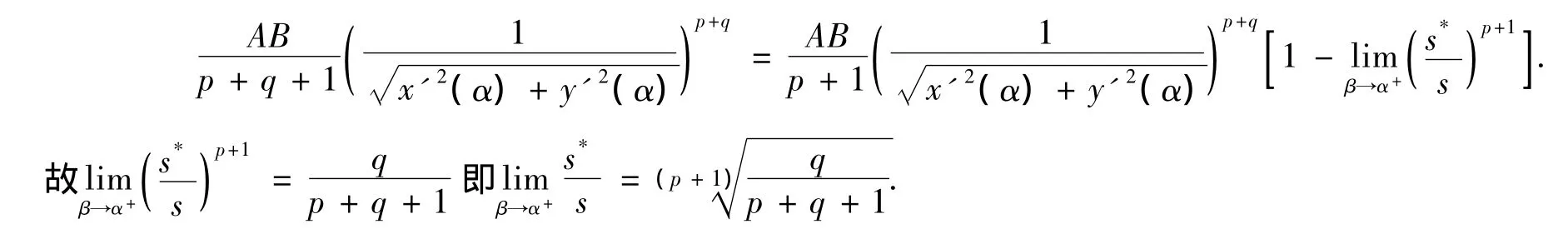
注:定理1中的“中間點”M［x(ζ)，y(ζ)］∈C(A，B)，s*，s分別是曲線C(A，M)和C(A，B)的長.上述的通式為,當時q=1，即其中實數p＞－1，則該通式可表示為，即當k(α)不為0其中q＞0，則通式可表示為;更特別的當q=1時，存在且不為0時，也即f(x，y)在當α的某領域存在一階導，g［x(α)，y(α)］≠0，即

證明:考慮光滑曲線C(A，B):x(t)=t，y(t)=0(α≤t≤β)，在曲線C(A，B)上，g［x(t)，y(t)］=g(t)，f［x(t)，y(t)］=f(t由題意知，g(t)在［α，β］上連續可積，f(t)是［α，β］上單調連續曲線積分化為了區間［α，β］上的積分，即定理2中的

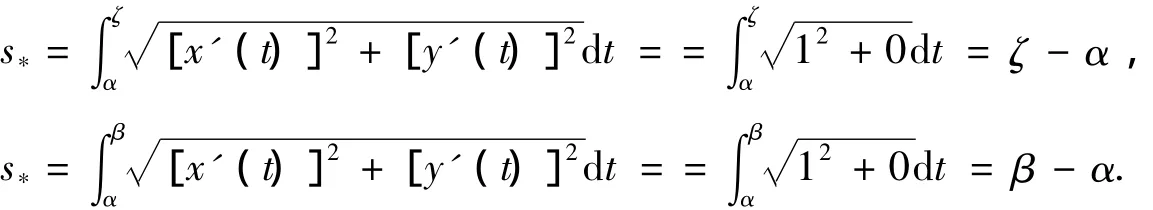
由定理2，可知積分第二中值定理的“中間點”ζ有漸近性

定理3如果曲線C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函數g(x，y)是曲線C(A，B)上的連續函數，f(x，y)是曲線C(A，B)上關于參數t單調的連續函數，并且h(i)(α)=0，(i=1，2，…，n－1)，hn(α)=0，k(m－1)(α)≠0，k(j)(α)=0(j=0，1，…，m－2)這里k(t)=g［x(t)，y(t)］，h(t)=f［x(t)，y(t)］，那么定理1中的“中間點M［x(ζ)，y(ζ)］∈C(A，B)有漸近性*，其中s，s分別是曲線C(A，M)和C(A，B)的長。

證明:由于函數h(t)=f［x(t)，y(t)］在點α處存在n階導數，則函數h(t)在點α處帶有Peano型余項的泰勒展開為

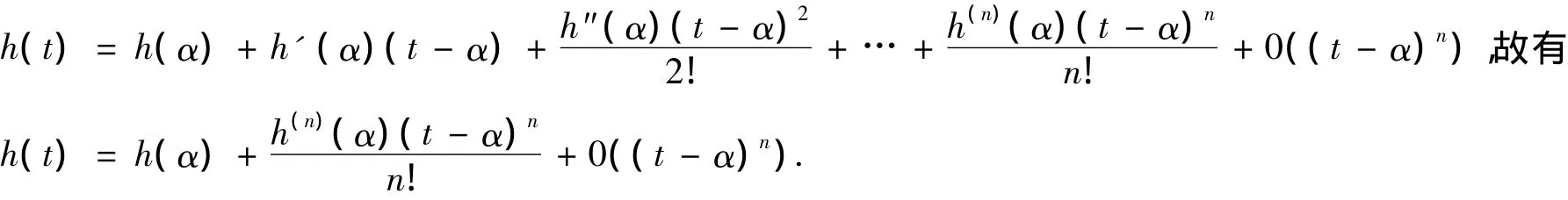
同理，函數k(t)=g［x(t)，y(t)］在點α處存在m－1階導數，則函數k(t)在點α處帶有Peano型余項的泰勒展開得到

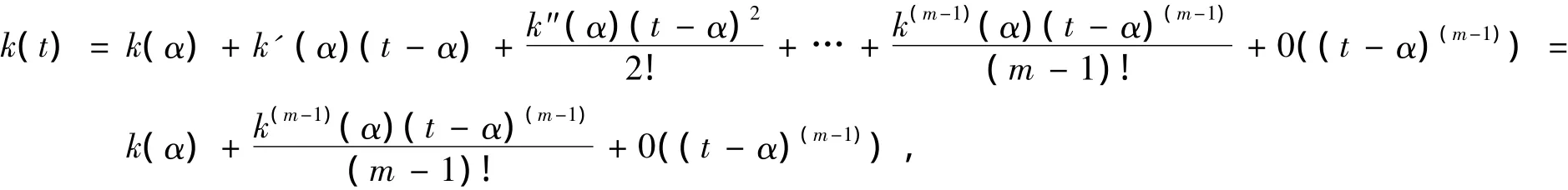
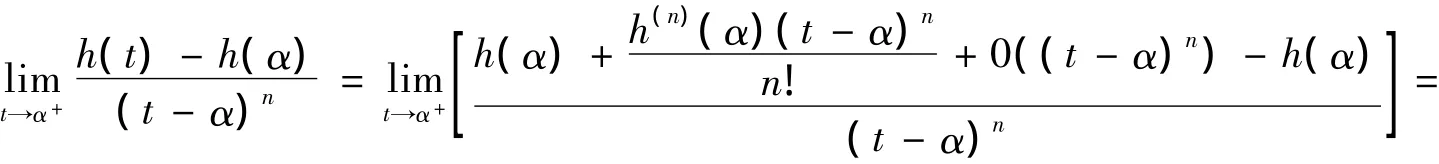
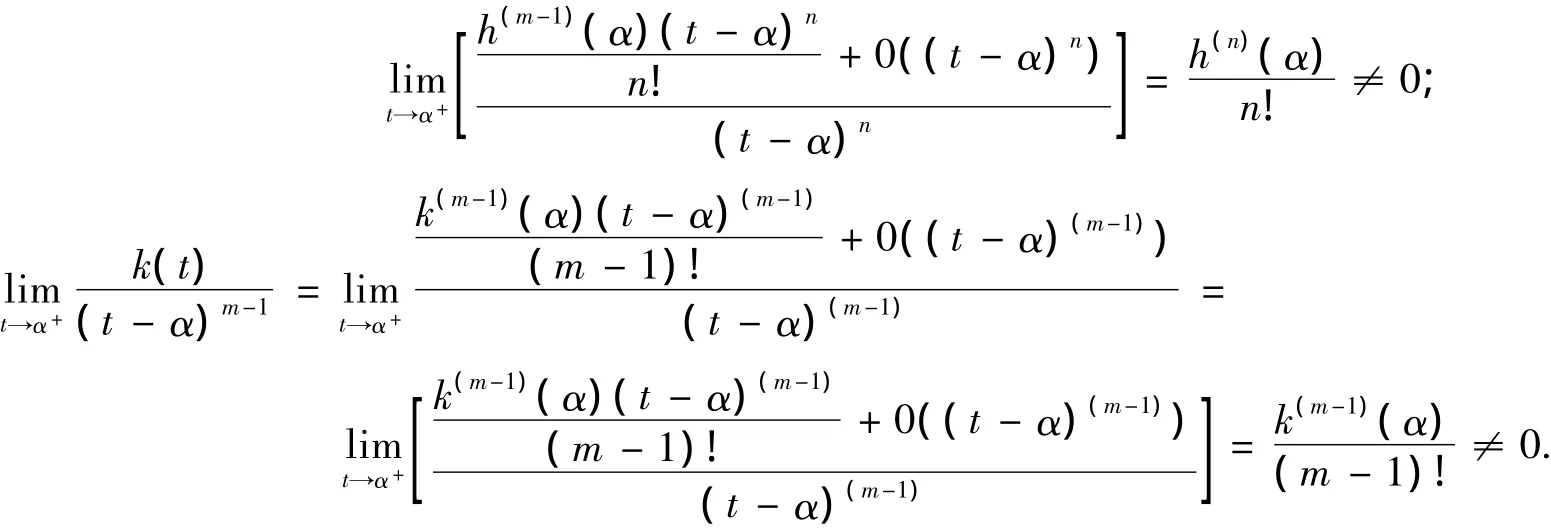
由定理2可知定理1中的“中間點”M［x(ζ)，y(ζ)］∈C(A，B)有漸近性，其中s*，s分別是曲線C(A，M)和C(A，B)的長。

注:定理1中的“中間點”M［x(ζ)，y(ζ)］∈C(A，B)，s*，s分別是曲線C(A，M)和C(A，B)的長.上述的通式，當n=1時，即f(x，y)存在一階可導，g(x，y)存在直到m－1導時，該通式可表示當m=1時，即g(x，y)當β→α時連續不可導，f(x，y)存在直到n導時，即該通式可表示為

推論［1］若函數g(x)在［α，β］上連續且不變號，f(x)在［α，β］上單調且連續，fn(α)存在，且f(i)(α)=0(i=1，2，…，n－1)，f(n)(α)≠0，n≥1，g(m－1)(α)≠0，g(j)(α)=0，(j=0，1，…，m－2)，ζ是積分第二中值定理的“中間點”，則

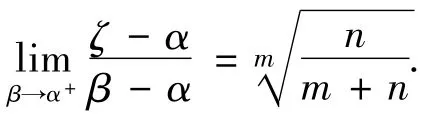
證明:考慮光滑曲線C(A，B):x=x(t)，y(t)=0(α≤t≤β)，在曲線C(A，B)上，g［x(t)，y(t)］=g(t)，f［x(t)，y(t)］=f(t)由題意知，g(t)在［α，β］上連續且不變號，f(t)在［α，β］上單調且連續，f(n)(α)存在，且f(i)(α)=0(i=1，2，…，n－1)，f(n)(α)≠0，n≥1，g(m－1)(α)≠0，g(j)(α)=0(j=0，1，…，m－2)

曲線積分化為了區間［α，β］上的積分，即定理3中的

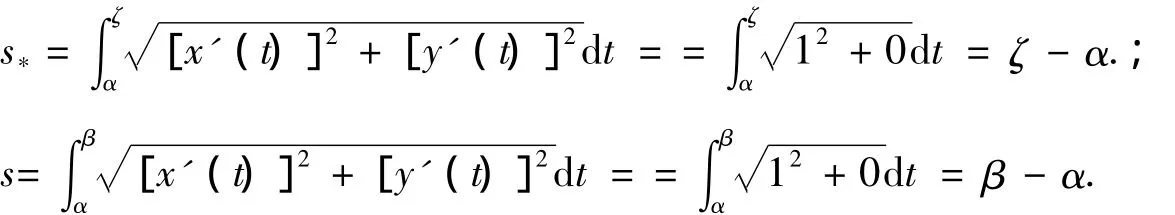
由定理3，可知積分第二中值定理的“中間點”ζ有漸近性

以上的推論是曲線積分第二中值定理“中間點”的漸近性在定積分第二中值定理“中間點”的漸近性的推廣。

［1］吳俊，嚴平.關于第二積分中值定理中的漸近性［J］.安徽師范大學學報(自然科學版)，1999，22(2):111－113.

［2］吳至友，夏雪.積分第二中值定理中間點的漸近性［J］.數學的實踐與認識，2004，34(3):170－176.

［3］劉文武.積分第二中值定理的一個一般性結果［J］.河南科技大學學報(自然科學版)，2005，26(5):90－92.

［4］華東師范大學數學系.數學分析(上冊)(第三版)［M］.北京:人民教育出版社，2001.

［5］楊彩萍，賈云暖.關于積分中值定理的一個一般性結果［J］.數學的實踐與認識，2002，32(4):670－698.

［6］鄭權.積分第二中值定理的中間點的漸近性質［J］.大學數學，2005，21(6):113－115.

［7］張鳳霞.曲線積分中值定理中間點的漸近性［J］.商丘師范學院學報，2001，17(4):107－109.

［8］裴東林.曲線積分中值定理中間點的漸近性的一個注記［J］.甘肅教育學院學報(自然科學版)，2003，17(4):13－15.［9］劉孝書.第一型曲線積分中值定理中間點的漸近性［J］.廣西右江民族師專學報，2005，18(6):1－5.

［10］趙益坤，節存來，王磊.關于曲線積分中值定理中間點的一個一般性質［J］.大學數學，2007，23(1):166－169.

［11］菲赫金哥爾茨，ГМ.微積分學教程［M］.北京:人民教育出版社，1956.

［責任編輯劉景平］

On Asym ptotic Property of the Mid－point of the Second Mean Value Theorem for First Form Curve Integral

LIN Dong－cui
(Guangxi College for Preschool Education，Nanning，Guangxi530022，China)

The asymptotic property of themid－pointof the second mean value theorem for first form curve integral is investigated．Then the result is generalized to the asymptotic estimation for themiddle pointof the second integralmean value．This conclusion is derived from the corresponding results of the definite integral of the second mean value theorem．By using the first curve points，themean pointof the secondmean value theorem for first kind curve integral is discussed．Finally the conclusions in this article extend those in［1］，［2］and［3］．

first form curvilinear integral;mean value theorem;mid－point;asymptotic property;

book=0,ebook=21

O175

A

1672－9021(2012)02－0065－07

林冬翠(1977－)，女(壯族)，廣西南寧人，廣西幼兒師范高等專科學校公共基礎部講師，主要研究方向:理論數學。

2011－10－26