自反矩陣下矩陣方程AXB+CXD=E的最佳逼近解
孫合明,李慶芳,楊家穩
(1.河海大學理學院,南京 210098;2.滁州職業技術學院,江蘇滁州 239000)
首先介紹本文中的一些符號。Rm×n表示m×n階矩陣的集合。I表示單位矩陣。AT表示矩陣A的轉置矩陣。對于矩陣A,B∈Rm×n,A?B表示A與B的Kronecker積,〈A,B〉=trace(BTA)定義為它們的內。‖A‖表示矩陣A的Frobenius范數,即‖A‖2=〈A,A〉。vec(·)是矩陣A=(aij) ∈Rm×n的拉伸算子,定義為
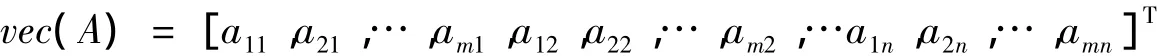
矩陣P若滿足PT=P和P2=I,則稱P是反射矩陣。對反射矩陣P∈Rm×m和Q∈Rn×n,若有A=PAQ,則稱矩陣A∈Rm×n是關于(P,Q)的廣義自反矩陣,并把所有 m×n階(P,Q)廣義自反矩陣的全體表示為(P,Q)。
本文主要考慮如下問題:
問題 1 對于給定的實矩陣 A,C∈Rs×m,B,D∈Rn×t,E∈Rs×t,求 X∈(P,Q),使得

問題2 設問題1的解集合為SE,對于給定(P,Q),求,使得
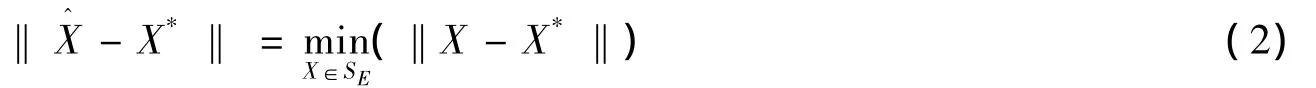
矩陣方程在控制和通信理論有著重要作用,在計算數學方面也是一個非常活躍的研究專題。問題2來源于常見的實驗設計,這里矩陣X*可由實驗獲得,它可能不是矩陣方程AXB+CXD=E的解。
文獻[1-2]提出了幾種解決矩陣方程AX+XB=C的方法。文獻[3]給出了矩陣方程AXAT+BXBT=C的對稱解。在矩陣方程ATXB+BTXTA=D相容的情況下,文獻[4]給出了它的極小范數解。在矩陣方程ATXB+BTXTA=D不相容的情況下,文獻[5]給出了求解給定矩陣最佳逼近解的一種算法,文獻[6-7]分別給出了其最小二乘解和極小范數最小二乘解。文獻[8]給出了求解矩陣方程AXB+CXTD=E極小范數最小二乘解的迭代方法。文獻[9]給出了矩陣方程AXB+CXD=F相容情況下的中心對稱最佳逼進解。關于反射矩陣P的自反(反自反)矩陣在系統和控制理論、工程、科學計算等多個領域都有廣泛的應用[10-11]。目前,已有越來越多的學者致力于研究矩陣方程的自反(反自反)最佳逼近解[12-13],但是還沒有文獻涉及求解矩陣方程AXB+CXD=E的自反(反自反)最佳逼近解。
本文在線性系統解集標準正交基的基礎上,給出了集合SE的表示形式,繼而在集合SE中給出問題2的最佳逼近解的表達式,最后通過2個數值實例驗證該算法的有效性。
1 問題1和問題2的解
本節利用矩陣零空間的標準正交基,給出問題1和問題2解的表達方式。
問題1是一般的約束優化問題,由于給定的目標函數和約束函數的特殊性,可以給出問題1解的表達方式。
定理 1 X=PXQ 等價于 vec(X)=B1x,其中 B1=(ξ1,…,ξr),x=(x1,x2,…,xr)T,ξ1,ξ2,…,ξr是矩陣(QT?P-I)零空間的標準正交基。
證明 由自反矩陣的定義有
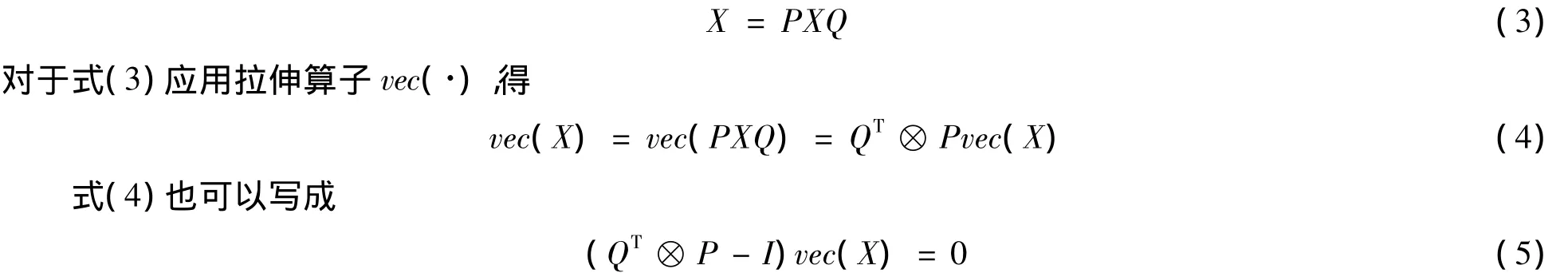
設ξ1,…,ξr是矩陣(QT?P-I)零空間的標準正交基,則式(5)的任意解vec(X)可以表示為故得式(6)。
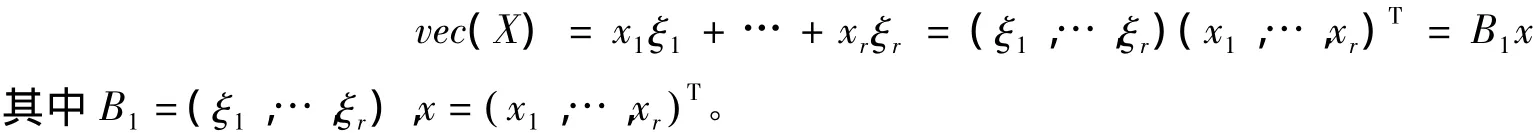

定理 3 問題 1 的最優解可以表述成 vec(X)=B1B2y+t,其中 y=(y1,y2,...,ys)T,B2=(η1,…,ηs),t=B1T,η1,…,ηs是矩陣A'B1零空間的標準正交基,T 是方程A'B1x=b'的一個特解,B1,A',c'如定理1和定理2所述。
證明 將vec(X)=B1x代入ψ(vec(X))=‖AXB+CXD-E‖2,得到
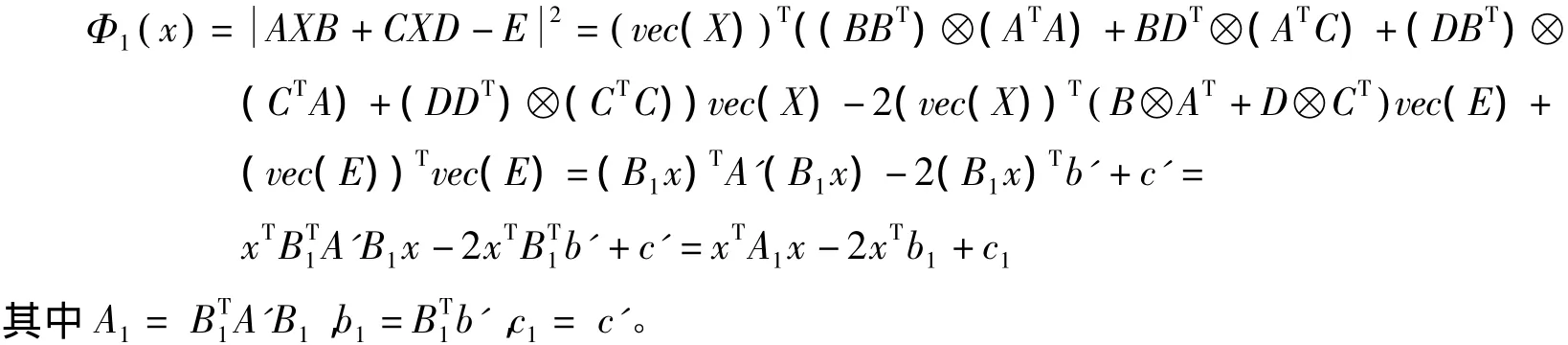
要使Φ1(x)取得極值,必有▽Φ1(x)=2A1x-2b1=0,得A1x=b1。設η1,…,ηs是矩陣A1零空間的標準正交基,T 是 A1x=b1的一個特解,則 x=(η1,…,ηs)(y1,…,ys)T+T=B2y+T,其中 y=(y1,y2,…,ys)T,B2=(η1,…,ηs),則問題1的最優解可以表述為 vec(X)=B1x=B1(B2y+T)=B1B2y+t,其中t=B1T。
定理4 設B1,B2分別是定理1和定理3中的列滿秩矩陣,則B1B2是列滿秩矩陣。
證明 B1是(p2+q2)×r列滿秩矩陣,則必存在一個r×r的滿秩矩陣U和一個r×r的單位矩陣Ir,
使得

定理5 設VX*=vec(X*),其中X*是給定的矩陣,則問題2的解為
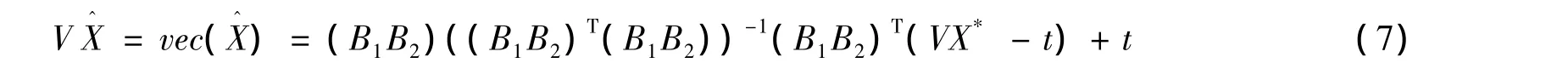
其中B1、B2、t分別如定理1和定理3所述。
證明 根據定理3,問題1的最優解為VX=vec(X)=B1B2y+t。設
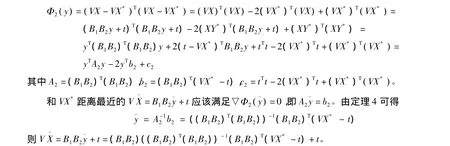
注釋1
2)對于問題1和問題2,如果限制矩陣X和Y屬于反自反矩陣集合,那么通過類似的方法可以求得它的反自反最佳逼近解。
2 數值測試
選取2個實例來驗證本文的算法。試驗均在Matlab 2007R上進行。
例1 考慮方程AXB+CXD=E,其中
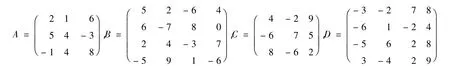

可以證明上述方程是相容的,有唯一自反矩陣解
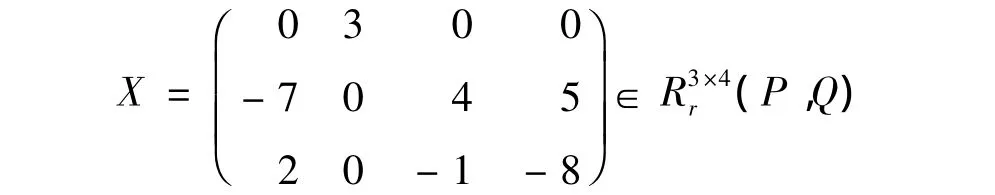
應用式(7),可以直接得到如下解:

相應的誤差R=‖A X^B+C X^D-E‖=5.070248950780553e-012。例1有力地說明了本文所給解的表達式的正確性。


3 結束語
本文借助于矩陣零空間的標準正交基,首先給出約束條件的解的一般表達式,繼而得到問題1的解的表達式。根據函數取得極值的必要條件,最后得出問題2的最佳逼進解的表達式。該表達式簡單明了,無需迭代即可直接計算出結果。對任意給定的矩陣,無論矩陣方程是否相容,運用本文給出的解的表達式都可以求出方程AXB+CXD=E的最佳逼近解。本文給出的2個數值實例有力地證明了該表達式的有效性。
[1]Richard H B,Stewart G W.Solution of the Matrix Equation AX+XB=C(Algorithm 432)[J].Commun ACM,1972,22:820-826.
[2]Golub G H,Nash S,Van Loan C.A Hessenberg-Schur method for the problem AX+XB=C[J].IEEE Trans Automat Control AC,1979,24:909-913.
[3]Chang X W,Wang J S.The symmetric solution of the matrix quations,AXAT+BXBT=C and(ATXA,BTXB )=(C,D)[J].Linear Algebra Appl,2000,311:67-78.
[4]袁永新.兩類矩陣方程的極小范數解[J].高等學校計算數學學報,2006,24(2):127-134.
[5]盛興平,蘇友峰,陳果良.矩陣方程ATXB+BTXTA=D的極小范數最小二乘解的迭代算法[J].高等學校計算數學學報,2008,30(4):352-362.
[6]袁永新.矩陣方程的最小二乘解[J].高等學校計算數學學報,2001,23(4):324-329.
[7]袁永新,戴華.矩陣方程ATXB+BTXTA=D的極小范數最小二乘解[J].高等學校計算數學學報,2005,27(3):232-238.
[8]Minghui Wang,Xuehan Cheng,Musheng Wei.Iterative algorithms for solving the matrix equation AXB+CXTD=E[J].Applied Mathematics and Computation,2007,187:622-629.
[9]劉大瑾,周海林,袁東錦.AXB+CXD=F的中心對稱解及其最佳逼近的迭代算法[J].揚州大學學報,2008,11(3):9-13.
[10]Chen H C.Generalized reflexive matrices:special properties and applications[J].SIAMJ MatrixAnal Appl,1998,19:140-153.
[11]Chen H C,Sameh A.Numerical linear algebra algorithms on the cedar system[C]//Parallel Computations and their Impact on Mechanics,AMD.[S.l.]:The American Society of Mechanical Engineers,1987:101-125.
[12]Xiang-yang Peng,Xi-yan Hu,Lei Zhang.The reflective and anti-reflective solutions of the matrix equations AHXB=C[J].Journal of Computational and Mathematics,2007,200:749-760.
[13]Zhen-yun Peng,Xi-yan Hu.The reflective and anti-reflective solutions of the matrix equation AX=C[J].Linear Algebra and Appl,2003,375:147-155.

