可加模型的序列相關(guān)性檢驗(yàn)

劉 鋒，李 飛，喬靜然

(重慶理工大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，重慶 400054)

可加模型是Ezekiel首先提出來(lái)的一種重要的非參數(shù)模型。Breiman和 Friedman、Bujia、Hastie和 Tibshiran、Ansley和 Kohn以及 Opsomer和 Ruppert等［1－8］諸多學(xué)者研究了向后擬合算法的收斂速度。Stone［9］估計(jì)了可加模型的最優(yōu)收斂速度。Wand［10］證明了局部多項(xiàng)式向后擬合算法估計(jì)量的中心極限定理。近幾年來(lái)，也有許多學(xué)者致力于可加模型的研究，比如Jiang和Li給出了可加模型非參數(shù)部分的2階段局部M－估計(jì)。綜上所述，目前對(duì)于可加模型的研究都集中在模型的估計(jì)和收斂速度方面。在對(duì)模型進(jìn)行估計(jì)之前，對(duì)模型進(jìn)行序列相關(guān)性檢驗(yàn)是十分必要的［11］。

對(duì)于一個(gè)擬合得好的模型，一般要求模型的殘差項(xiàng)是一列獨(dú)立同分布的白噪聲，只有滿足此假定，方可對(duì)模型進(jìn)行估計(jì)。本文正是基于這方面的考慮，引入了VT，P方法對(duì)可加模型中的序列相關(guān)問(wèn)題進(jìn)行檢驗(yàn)，得到了零假設(shè)下VT，P檢驗(yàn)統(tǒng)計(jì)量的漸近分布，并用數(shù)值模擬驗(yàn)證了檢驗(yàn)的功效。

1 方法與主要結(jié)果

考慮如下的部分線性單指標(biāo)模型:

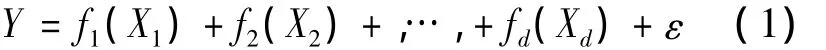
其中(X，Y)是獨(dú)立同分布的隨機(jī)變量。Xj(j=1，…，d)是X的第j個(gè)分量。X∈Rd，fj是未知函數(shù)。為了滿足模型的可識(shí)別要求，令E(fj(Xj))=0，容易看出當(dāng)fj(Xj)=βjXj時(shí)，式(1)其實(shí)就是多元線性回歸模型。

本文用VT，P檢驗(yàn)方法對(duì)模型(1)的序列相關(guān)性進(jìn)行檢驗(yàn)。首先構(gòu)造VT，P檢驗(yàn)統(tǒng)計(jì)量，令

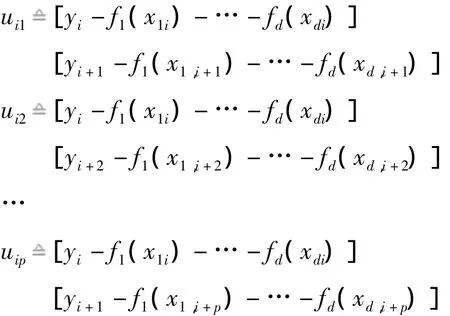
記T=n－p，根據(jù)Hu的研究得到了如下的VT，P檢驗(yàn)統(tǒng)計(jì)量。但該式中含有未知函數(shù)fj(·)，因而不能直接用于統(tǒng)計(jì)推斷。這時(shí)，在零假設(shè)下分別用它們的估計(jì)(·)來(lái)代替。令

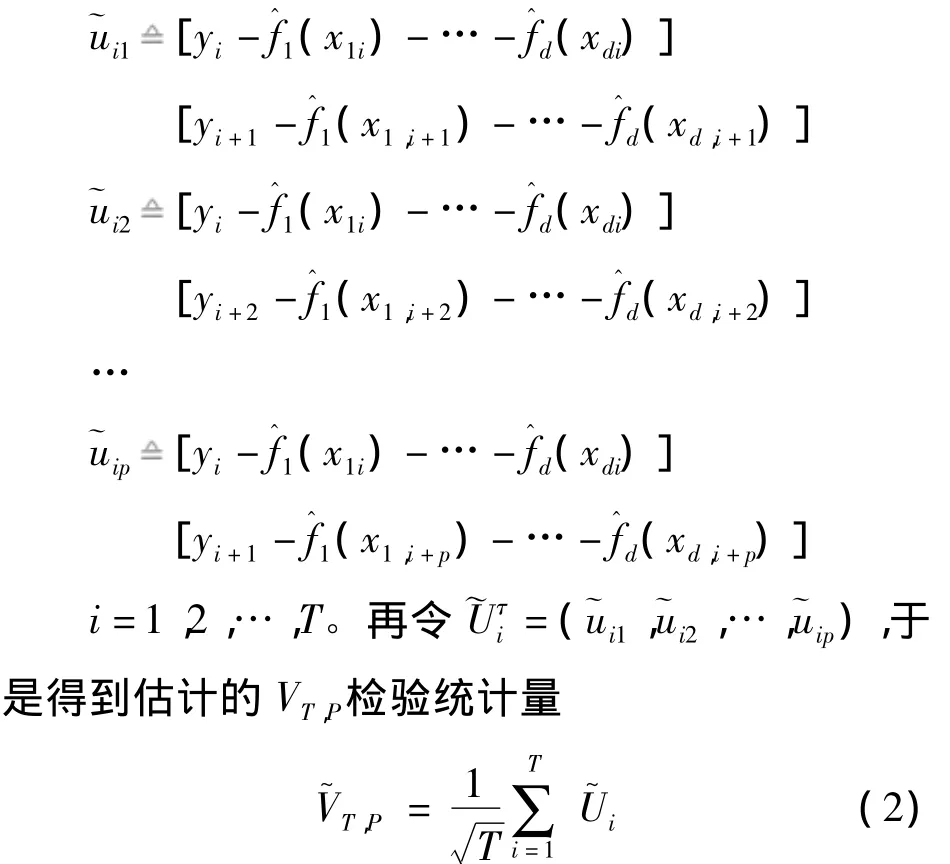
對(duì)于未知函數(shù)fj(·)的估計(jì)，采用局部多項(xiàng)式向后擬合算法來(lái)計(jì)算，其正規(guī)方程為

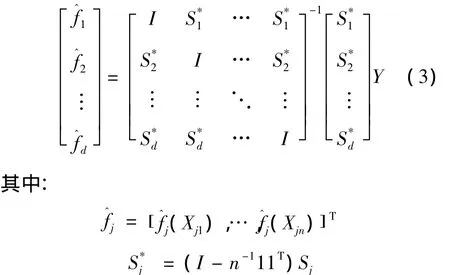
Sj是依賴于Xj1，…，Xjn的n階局部多項(xiàng)式平滑器矩陣。當(dāng)式(3)中的逆矩陣的維數(shù)比較大時(shí)，直接利用正規(guī)方程在普通的計(jì)算機(jī)上難以執(zhí)行，于是本文采用局部多項(xiàng)式向后擬合算法來(lái)實(shí)現(xiàn)，步驟如下:

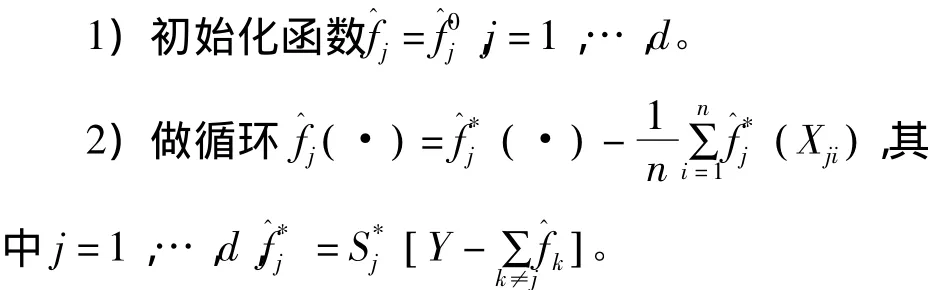
3)重復(fù)步驟2)，直到收斂為止。

本研究為了得到主要結(jié)果，需要如下條件:

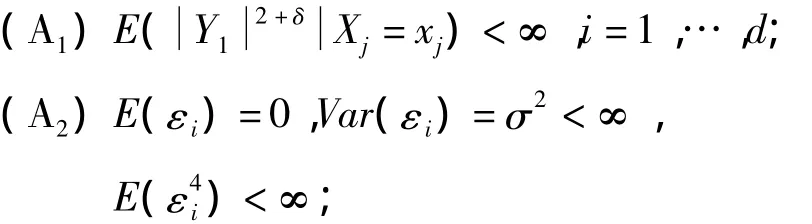
(A3)fj，i=1，…，d 是 p+1 階連續(xù)可導(dǎo)的;

(A4)概率密度函數(shù) fX1，X2，…，Xd和 fX1，fX2，…，fXd都是有界連續(xù)的，有緊支撐，并且

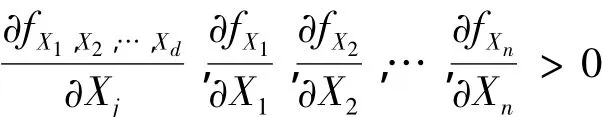
(A5)核函數(shù)K在它的支撐上是有界連續(xù)的，并且一階偏導(dǎo)數(shù)大于0;

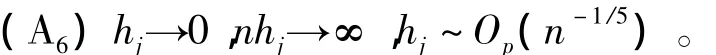
在上述條件下，有如下定理:

定理1 在條件A1～A6及零假設(shè)下，當(dāng)T→∞時(shí)，有(0，σ2Ip)，其中Ip是 p×p的單位矩陣，σ2=

2 數(shù)值模擬

通過(guò)一些數(shù)值模擬來(lái)考慮VT，P檢驗(yàn)的有限樣本性質(zhì)。為了簡(jiǎn)單起見(jiàn)，考慮下面的模型:

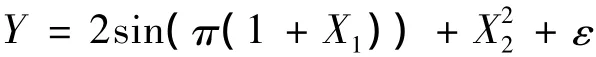
其中:ε與 X1、X2相互獨(dú)立;Z1和 Z2服從U(－1，1);X1=Z1+Z2，X2=Z1－ βZ2;β 為 Z1和Z2的相關(guān)系數(shù)。

假定誤差εi分別服從如下模型:

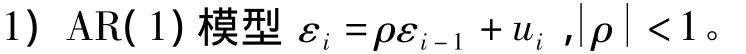
對(duì)于誤差模型1和2，樣本量分別選為50，100，200，顯著性水平選為0.05;對(duì)于誤差模型3和4，樣本量分別選為100，200，400，顯著性水平選為0.05，均做1000次模擬。模擬結(jié)果在表1～4中給出。

表1 檢驗(yàn)size和功效，誤差服從AR(1)模型

表2 檢驗(yàn)size和功效，誤差服從MA(1)模型

表3 檢驗(yàn)size和功效，誤差服從AR(2)模型

表4 檢驗(yàn)size和功效，誤差服從MA(2)模型

從表1～4中可以看出:當(dāng)樣本量小時(shí)，檢驗(yàn)的size有偏大的現(xiàn)象，但是隨著樣本量的增加，檢驗(yàn)的size迅速收斂到給定顯著性水平;而在備擇假設(shè)下，檢驗(yàn)的功效都很好。同時(shí)也可以看出，在樣本容量n相同的情況下，隨著模型誤差相依程度的不斷加大，這2種檢驗(yàn)方法的功效也隨之提高，在各種情況下，都有好的檢驗(yàn)功效。

3 定理1的證明

3.1 引理

在證明過(guò)程中，由于T=n－p，因此本文不區(qū)別Op(n)和Op(T)等。假定C為絕對(duì)常數(shù)，在不同的地方取值不同。為了證明定理1，先給出幾個(gè)引理。

引理1 在條件A1～A6和零假設(shè)下，有

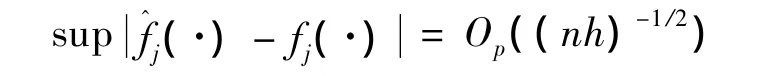
證明見(jiàn)文獻(xiàn)［10］。

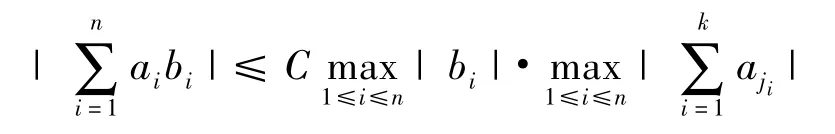
其中(j1，j2，…，jn)是(1，2，…，n)的任意排列。

引理3 設(shè) εi，i=1，2，…，n 是獨(dú)立隨機(jī)變量序列，滿足 Eεi=0＜∞，則有

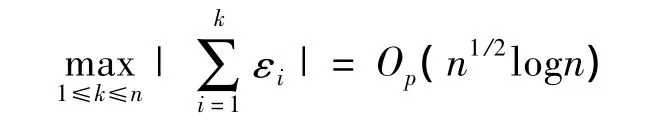
且對(duì)于(1，2，…，n)的任何一個(gè)置換(j1，j2，…，jn)，有

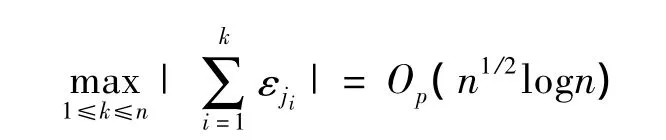
證明見(jiàn)文獻(xiàn)［5］。

3.2 定理1的證明

因?yàn)?/p>

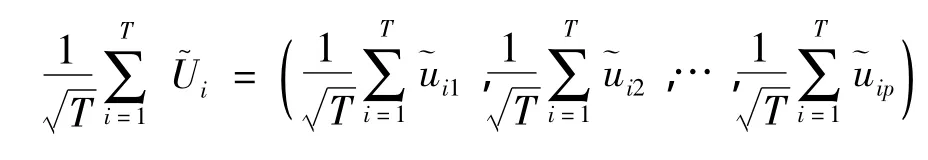
故對(duì)任意的整數(shù)k(1≤k≤p)，有:

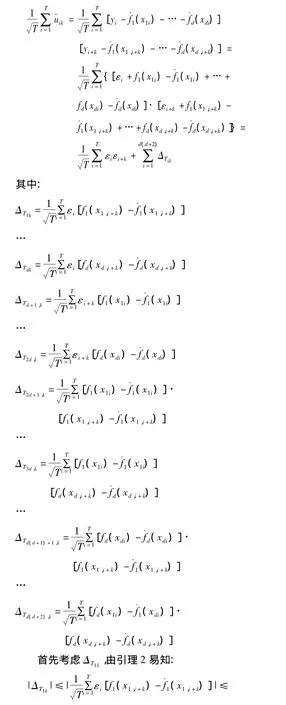
由Gramer-Wold方法，根據(jù)m步相依隨機(jī)變量中心極限定理可得

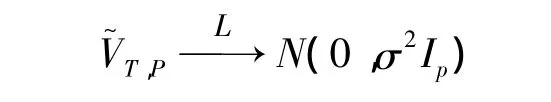
定理1得證。

［1］Ansley C F，Kohn R.Convergence of the backfitting algorithm for additive models［J］.Journal of the Australian Mathematical Society，Series A，1994，57:316-329.

［2］Buja A，Hastie T J，Tibshirani R.Linear smoothers and additive models［J］.The Annals of Statistics，1989，17:453-510.

［3］Ezekiel A.A method of handling curvilinear correlation for any number of variables［J］.Journal of American Statistical Association，1924，19:431-453.

［4］Fan J，Hardle W，Manmen E.Direct estimation of low-dimensional conponents in additive models［J］.The Annals of Statistics，1998，26:943-971.

［5］Gao J T.Asymptotic theory for partly linear models［J］.Communications in Statistic-Theory and Methods，1995，24:1985-2010.

［6］Hu X M，Liu F，Wang Z Z.Testing serial correlation in semiparametric varying coefficient partial linear errors-invariables models［J］.Jrl Syst Sci Complexity，2006，22:483-494.

［7］Jiang J，Li J.Two-stage local M-estimation of additive models［J］.Science in China，Series A:Mathematics，2008，51:1315-1338.

［8］Opsomer J D，Ruppert D.Fitting a bivariate additive model by local polynomialregression［J］.The Annals of Statistics，1997，25:186-211.

［9］Stone C J.Additive regression and other nonparametric models［J］.The Annals of Statistics，1985，13，689-705.

［10］Wand M P.A central limit theorem for local polynomial backfitting estimators［J］.Journal of Multivariate Analysis，2000，70:57-65.

［11］劉鋒，陳敏，鄒捷中.部分線性模型序列相關(guān)的經(jīng)驗(yàn)似然比檢驗(yàn)［J］.應(yīng)用數(shù)學(xué)學(xué)報(bào)，2006，29:577-586.