關于GA-凸函數的Hadamard型不等式的一個注記
時統(tǒng)業(yè),吳 涵
(海軍指揮學院浦口分院,南京 211800)
1 引理
定義 1[1]設 f(x)是定義在區(qū)間 I?(0,+ ∞)上的連續(xù)函數,如果對于任意 a,b∈I和 t∈(0,1),有

則稱f(x)在區(qū)間I是GA-下凸的。如果式(1)的不等號反向,則稱f(x)在區(qū)間I上是GA-上凸的。
文獻[2-4]給出關于GA-凸函數的Hadamard型不等式,見定理1。
定理 1[3-4]設 f(x)是[a,b]上的 GA - 下凸函數,則
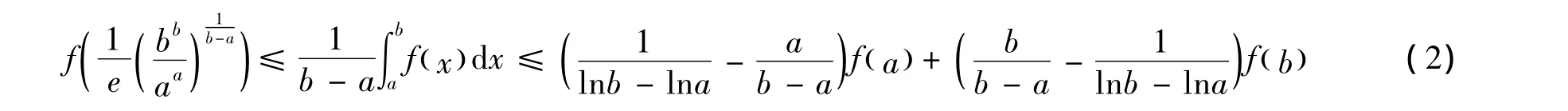
如果f(x)是[a,b]上的GA-上凸函數,則式(2)的不等式反向。當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
注1 由定理1的證明過程易知
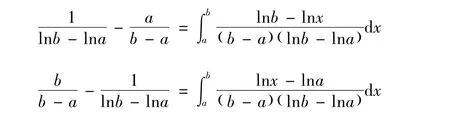
引理1[1]設f(x)是定義在[a,b]?(0,∞)上的函數,則f(x)是[a,b]上的GA -下凸函數的充要條件為f(ex)為[lna,lnb]上的下凸函數。
引理 2[5]設 f(x)是[a,b]上的下凸函數,則對任意 x,y∈[a,b],有
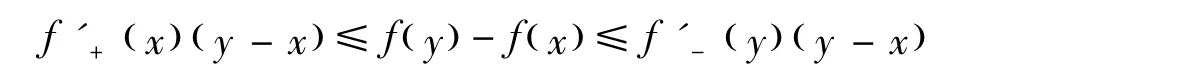
當且僅當f(x)=c+dx時等號成立,c、d是常數。
引理3 設f(x)是定義在[a,b]?(0,∞)上的GA-下凸函數,則
1)x f'-(x)和 x f'+(x)在(a,b)單調不減。
2)對任意 x,y∈[a,b],有
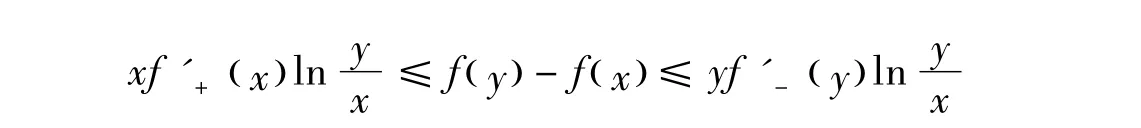
當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
證明 令h(x)=f(ex),那么
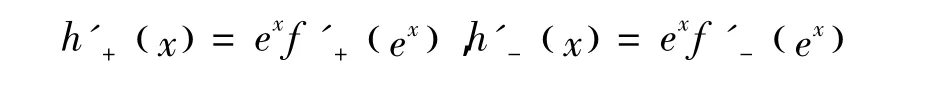
因為 f(x)是[a,b]?(0,∞)上的 GA -下凸函數,由引理1知,h(x)是[lna,lnb]上的下凸函數。根據下凸函數的性質知h'-(x)與h'+(x)在(a,b)單調不減,也即 xf'-(x)和xf'+(x)在(a,b)單調不減。又由引理 2 知,對任意 u,v∈[lna,lnb],有
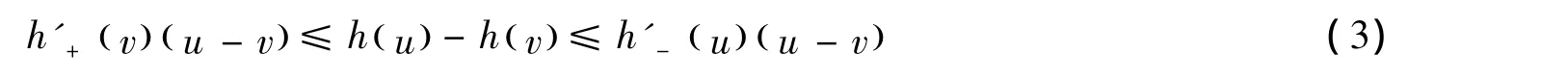
在式(3)中取u=lny,v=lnx,則引理3結論2)得證。
引理4 設f(x)是定義在[a,b]?(0,+∞)上的連續(xù)的GA-下凸函數,則有
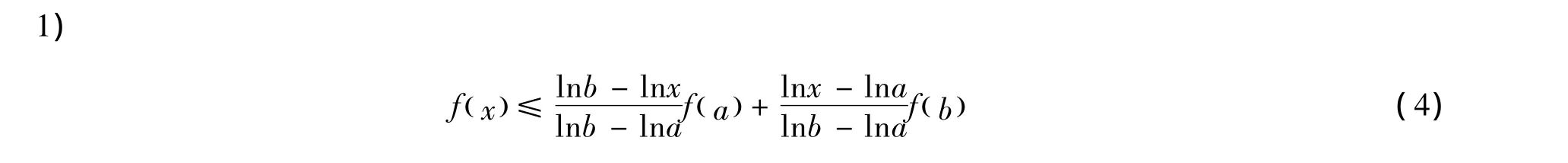
當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
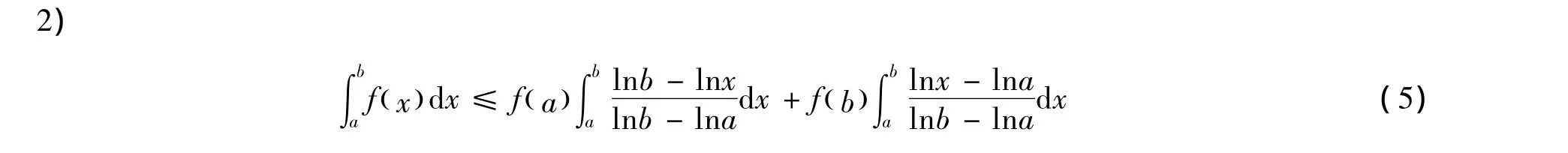
當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
證明 對任意 x∈[a,b],有
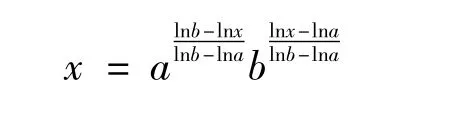
由GA-下凸函數的定義得式(4)。式(4)在[a,b]上取積分得式(5)。
設 f(x)是定義在(a,b)上的可導的下凸函數,對于任意 x1,x2∈[a,b],x1<x2,文獻[6]證明了下面結果:
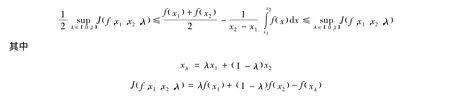
本研究將仿照文獻[6]的方法,將上述結果移植到GA-下凸函數。設0<x1<x2,λ∈(0,1),引入記號
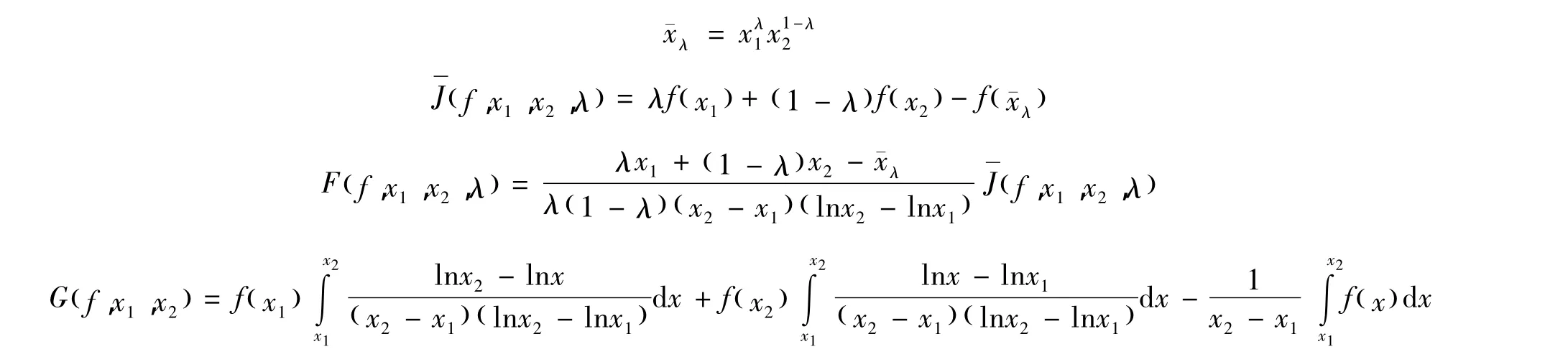
本研究的主要結果:
定理2 設 f(x)是定義在(a,b)上的可導的 GA -下凸函數,對于任意 x1,x2∈(a,b),x1<x2,有
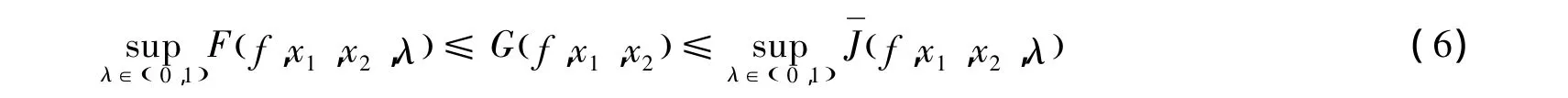
當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
2 定理2的證明
由引理4得
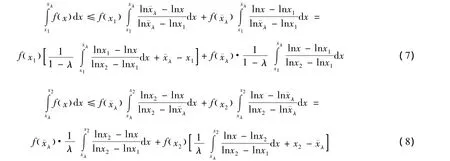
式(7)、(8)兩式相加得:

則式(6)的左端部分得證。
由Cauchy中值定理,存在τ∈(x1,x2),使得

由引理3 知,對于任意 x∈[x1,x2],有

式(13)的兩邊對x在[x1,x2]上積分得

式(6)得證。
當f(x)=c+dlnx(c、d是常數)時,經簡單計算可知式(6)中的3項都為零,所以等號成立。反之,若式(6)的等號成立,則由上面的證明過程可知,必有式(14)等號成立,由引理4知,f(x)=c+dlnx(c、d是常數)。
推論1 設 f(x)是定義在(a,b)上的可導的 GA -下凸函數,對于任意 x1,x2∈(a,b),x1<x2,有
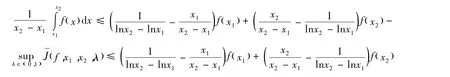
當且僅當f(x)=c+dlnx時等號成立,c、d是常數。
[1]吳善和.GA-凸函數與琴生不等式[J].貴州師范大學學報:自然科學版 ,2004,22(2):52-55.
[2]ZHANG X M,CHU Y M.A Double Inequality for the Gamma and Psi Functions[J].International Journal of Modern Mathematics,2008,3(1):23-27.
[3]華云.關于 GA-凸函數的Hadamard型不等式[J].大學數學,2008,24(2):147-149.
[4]張小明,褚玉明.解析不等式新論[M].哈爾濱:哈爾濱工業(yè)大學出版社,2009:198-203.
[5]匡繼昌.常用不等式[M].3版.濟南:山東科學技術出版社,2004:375-376.
[6]Zoran D.Mitrovi.A Remark on Hadamard’s Inequality[J].Applied Mathematical Sciences,2008,2(43):2127-2130.

