關于q-gamma函數及對數導數的性質

趙教練

(渭南師范學院數學與信息科學學院，陜西渭南714000)

經典分析中的Gamma函數是一類特殊的函數，是由L.Euler在18世紀推廣自然數的階乘時給出的，常被稱為第二類Euler積分，定義如下：

關于Gamma和q-gamma函數研究成果很多也很重要，它們在分析、數論、特殊函數論、數學物理方法等領域中都起著關鍵的作用［6-7］.本文在此基礎上，將給出q-gamma的一些新的性質.

1 主要引理

為了證明所給的結論，需要以下兩個引理：

引理1 對于給定的x＞0，有以下恒等式

證明 以上各恒等式很容易從定義中直接推出.

引理2 給定x∈［0，1］，q∈(0，1)并且0 ＜s＜1，我們有以下不等式成立

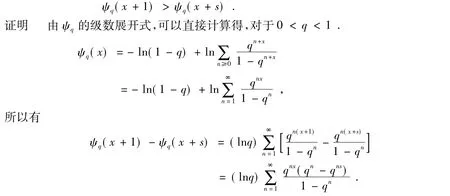
當0 ＜q＜1，x∈［0，1］，0 ＜s＜1，我們可以得到 ψq(x+1)－ ψq(x+s) ＞0.

2 定理及其證明

定理1 給定x∈［0，1］，q∈(0，1)并且0 ＜s＜1，我們有以下恒等式成立

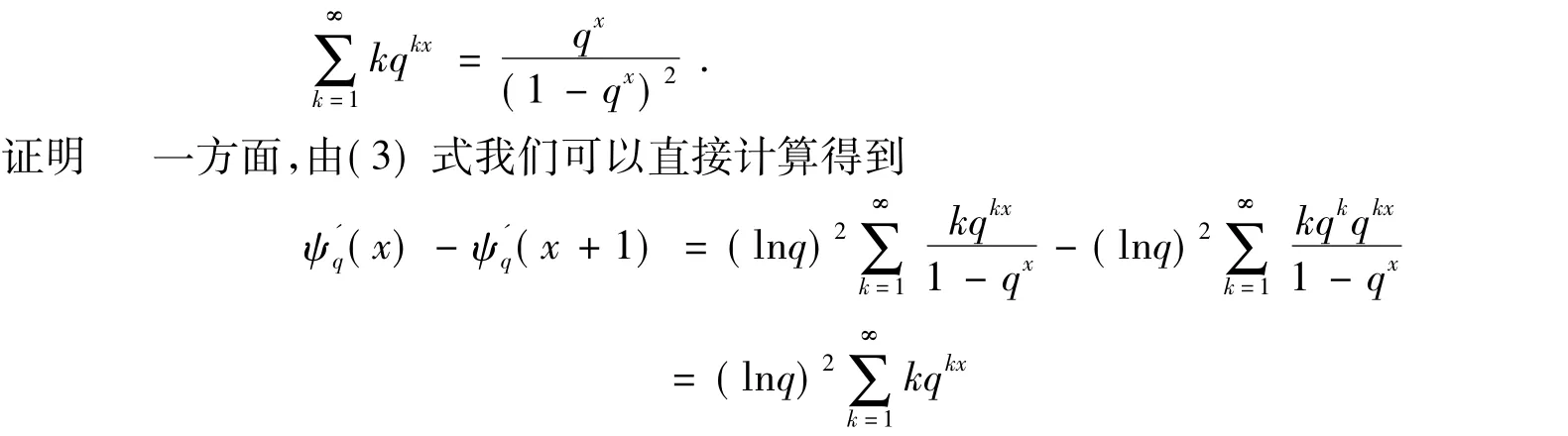
另一方面，由引理中第四式兩邊求導，比較上式可以證明所要的結論.

定理2 對于0＜q＜1，我們可以給出Gamma之商的一個不等式的q模擬，即

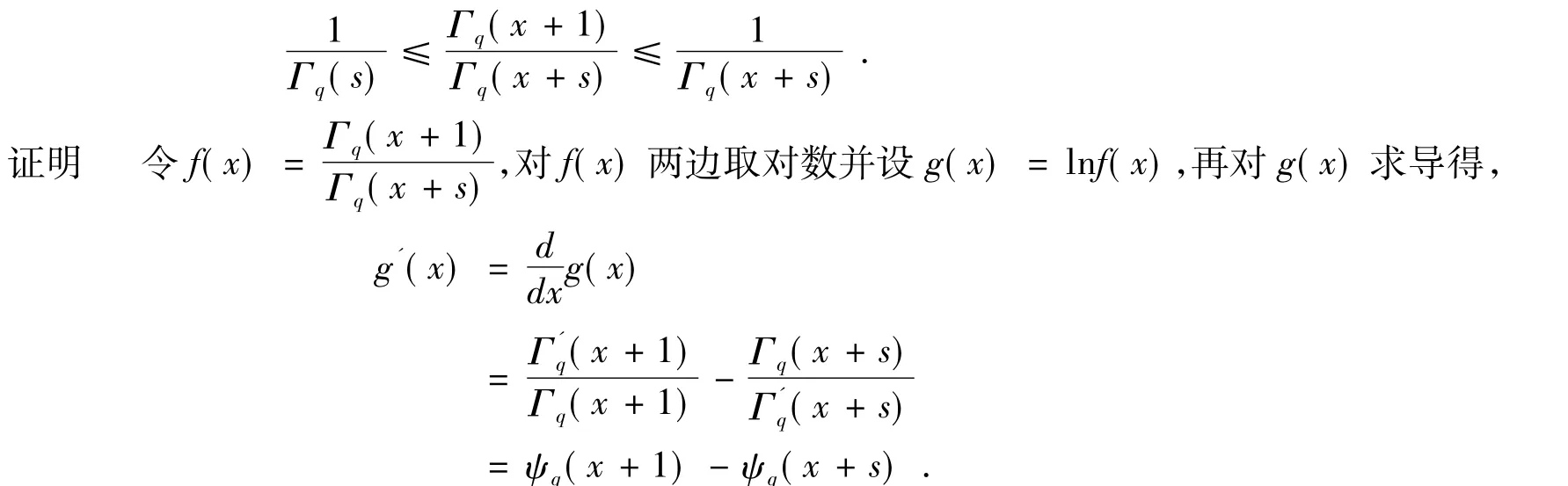
由上式計算的結果，根據引理1的結論，我們可以判斷g'(x)＞0，也就是得到g(x)是區間［0，1］上的單調遞增函數.所以f(x)也是區間［0，1］上的單調遞增函數，那么對于f(x)就有f(0)＜f(x)＜f(1)，也就是

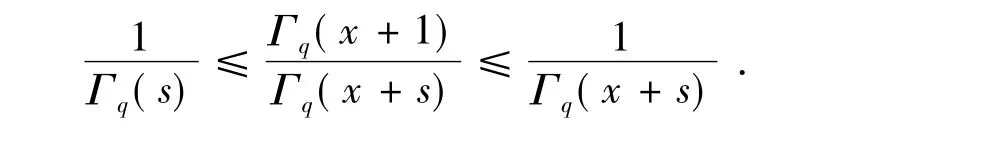
［1］Artin E.The Gamma function［M］.New York：Toronto，1964.

［2］Jensen J，Gronwall T.An elementary exposition of the theory of gamma function The Ann［J］.1916，17(3)：124 －166.

［3］Jackson F.H.A Generalization of the Functionsand Γ(n)and xn［J］.Proc.Roy.Soc.London，1904，74(1)：64 －72.

［4］Koornwinder T.H.Jacobi functions as limit cases of q-ultraspherical polynomials［J］.Math.Anal.Appl，1990，148：44 － 54.

［5］Krattenthaler C，Srivastava H.M.Summations for basic hypergeometric series involving a q-analogue of the digamma function［J］.Comput.Math.Appl，1996，32(3)：73 －91.

［6］Askey R.The q-gamma and q-beta functions［J］.Applicable Analysis，1978，8(2)：125 －141.

［7］Andrews G，Askey R，Roy R.Special Functions［M］.New York：Cambridge University Press，1999.

［8］王竹溪，郭敦仁.特殊函數概論［M］.北京：北京大學出版社，2000.