半E-預不變凸模糊數值函數及其刻劃

白玉娟

(隴東學院數學與統計學院，甘肅慶陽745000)

自從美國加州大學控制論專家Zadeh教授提出模糊集的概念以來，模糊數學作為一門新的數學學科得到了迅速的發展.經典凸分析理論與數學規劃等應用模型的研究是息息相關的.然而，正象許多系統中含有參數的不確定性，從而模糊優化問題已有很多討論，并促使了模糊凸分析理論的研究.關于模糊映射的凸性、擬凸性及B-凸性，文獻［1-3］已有討論，1994年，Noor［4］提出預不變凸模糊數值函數的概念，并討論了模糊數值函數的預不變凸性.1999年，Youness［5］提出了E-凸集和E-凸函數的概念，并討論了實值函數在E-凸集上的廣義凸性問題.但對預不變凸模糊數值函數的本質研究還需進一步深入，本文給出了半E-預不變凸模糊數值函數的定義，并討論了模糊數值函數在廣義凸集上的半E-預不變凸性.

1 預備知識

若模糊集u：R1→［0，1］是正規的，凸的，上半連續的且支撐集緊，則u稱為模糊數［6］.記F為R1上所有模糊數組成的集合.

設模糊數u，其水平截集是有界閉區間［u］α= ［u－(α)，u+(α)］，由文獻［6］知，u－(α)是［0，1］上非減的函數;u+(α)是［0，1］上非增的函數;u－(α)和u+(α)是有界的，在(0，1］上左連續，在α =0右連續且u－(1)≤u+(1).

反之，若函數u－(α)和u+(α)在［0，1］上滿足上述條件，則存在一個模糊數u∈F，使得［u］α=［u－(α)，u+(α)］(α ∈［0，1］).

記

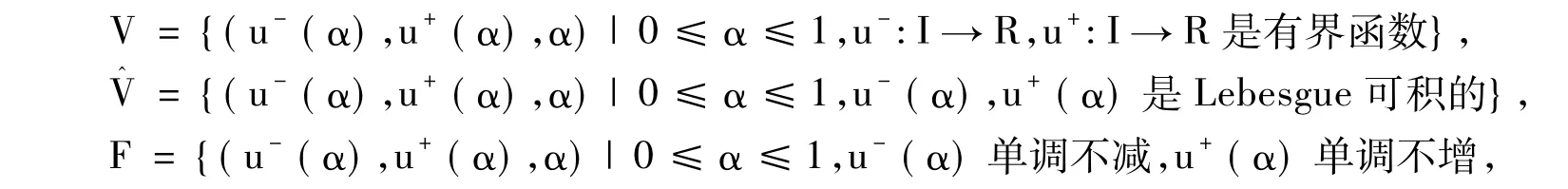
均左連續且在α=0處右連續}.

在V中定義和與數乘運算為［6］：

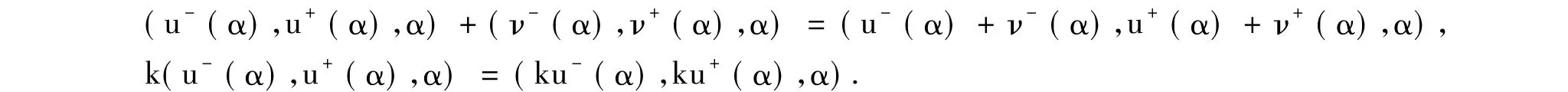
對于ui∈V^，ui={(u－i(α)，u+i(α))|α∈［0，1］}(i=1，2，…，n).稱模糊數(u1，u2，…，un)為n維模糊向量，記所有n維模糊向量的集合為V^n且定義Rn×V^n的直積為：

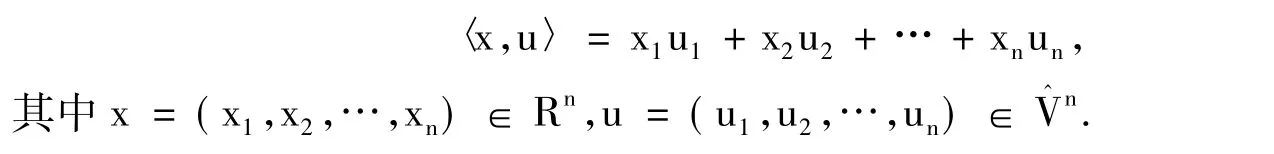
設 u，ν ∈ V^，u={(u－(α)，u+(α)，α)|0 ≤ α ≤1}，ν ={(ν－(α)，ν+(α)，α)|0 ≤ α ≤1}.稱u ≤ ν，如果α)(u-(α)+u+(α))dα ≤α)(ν-(α)+ ν+(α))dα .

對于模糊數值函數 F(x)={(F-(α，x)，F+(α，x)，α)|0 ≤ α ≤1}，記 TF(x)=α)［F-(α，x)+F+(α，x)］dα，其中f為［0，1］上單調不減的非負函數，滿足f(0)=1，且α)dα.f可以理解為權重函數，單調不減保證了越是接近模糊數的核的水平截集，在序關系的確定中作用越大.特別地，當f(α)=α時，退化為文獻［7］中的序關系.

2 半E-預不變凸模糊數值函數

定義1 設S(?Rn)是關于η：S×S→Rn的不變凸集，若存在映射E：Rn→Rn對任意的x，y∈S及λ ∈［0，1］，有

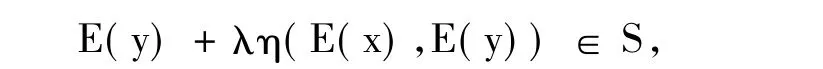
則稱S為E-不凸集.

定義2 設F：S→F為模糊數值函數，S(?Rn)是關于η：S×S→Rn的不變凸集，若存在映射E：Rn→ Rn對任意的 x，y∈ S 及 λ ∈［0，1］，有

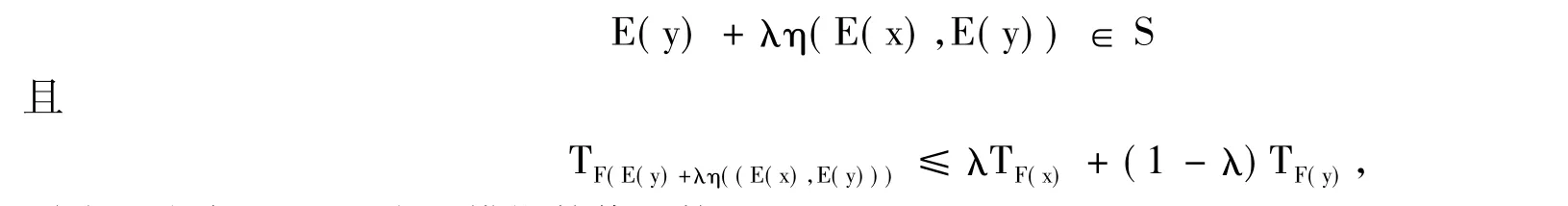
則稱F為半E-預不變凸模糊數值函數.

定理1 設F：S→F是E-不變凸集S上的半E-預不變凸模糊數值函數，則對任意的y∈S有TF(E(y))≤TF(y).

證明 由于F：S→F是E-不變凸集S上的半E-預不變凸模糊數值函數，則對任意的x，y∈S及λ∈［0，1］，有

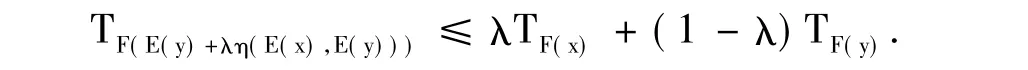
令λ =0，則對任意的y∈S有TF(E(y))≤TF(y).

定理2 設F：S→F是E-不變凸集S上的模糊值數值函數，則F是半E-預不變凸模糊數值函數當且僅當對任意的 x，y∈ S 及 λ ∈［0，1］和 u，ν ∈ F，當 TF(x)≤ Tu，TF(y)≤ Tν時，有

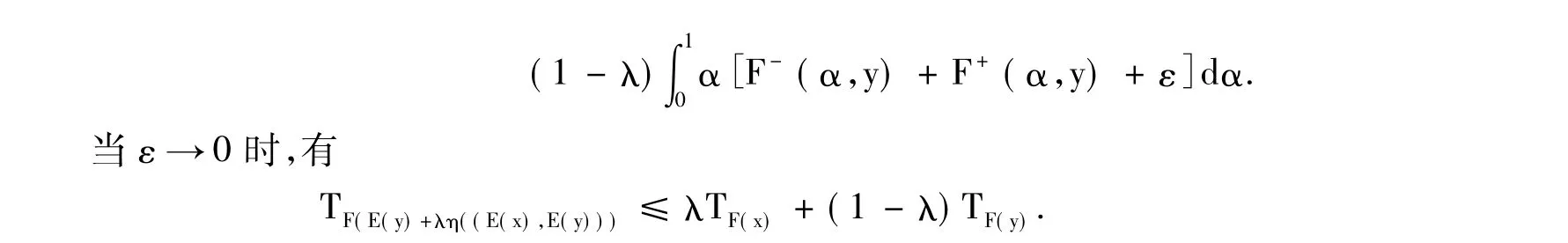
從而F是半E-預不變凸模糊數值函數.

定理3 設F：S→F是E-不變凸集S上的半E-預不變凸模糊數值函數，則對任意的u∈F，

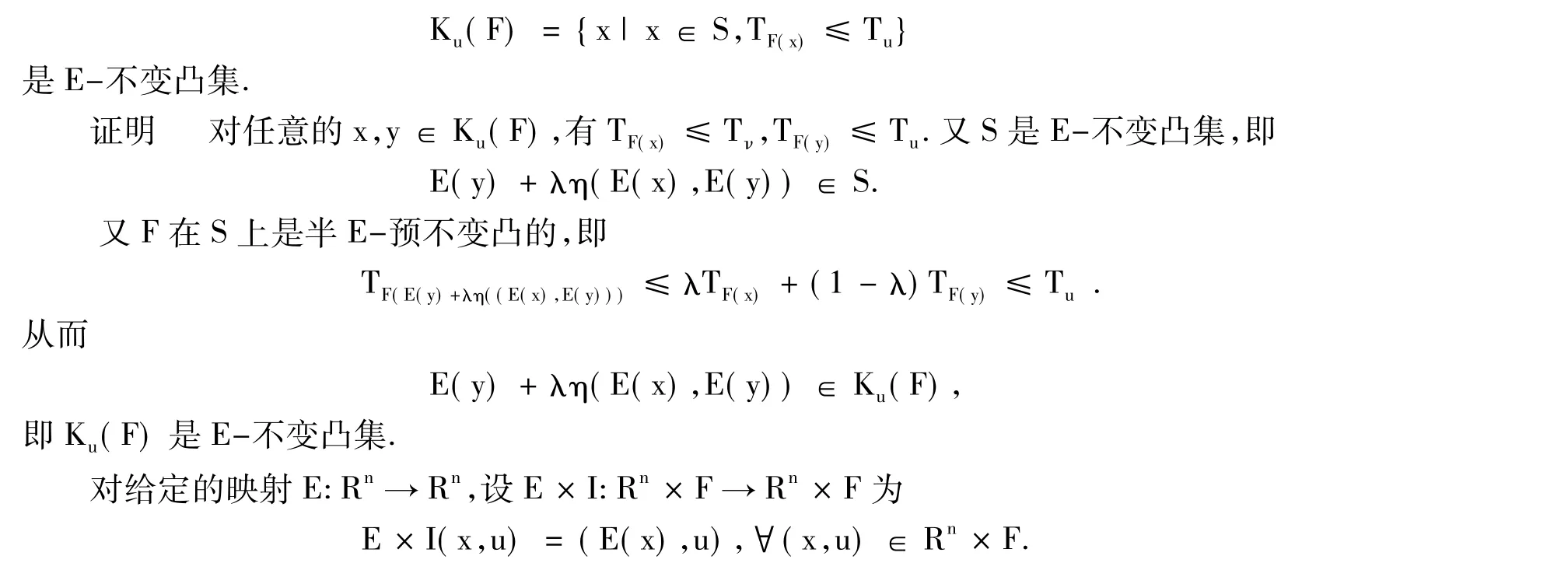
定義3 設S?Rn× F，若存在映射 E：Rn→Rn使得對任意的(x，u)(y，ν)∈S(x，y∈Rn，u，ν∈F)及 λ ∈［0，1］，有

E × I(y，ν)+ λη［E × I(x，y)，E × I(y，ν)］ = ［E(y)+ λη(E(x)，E(y))，λu+(1- λ)ν］∈ S，則稱S為Rn×F中的E×I-不變凸集.

定理4 設{Si}i∈J是Rn×F中的E×I-不變凸集，則∩i∈JSi也是Rn×F中的E×I-不變凸集.

證明 設(x，u)，(y，ν) ∈∩i∈JSi，λ ∈［0，1］，則對任意 i∈ J有

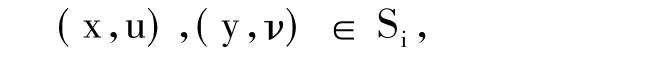
又因為每個Si是Rn×F中的E×I-不變凸集，即存在映射E：Rn→Rn使得對任意的(x，u)，(y，ν)∈Si及 λ ∈［0，1］，有

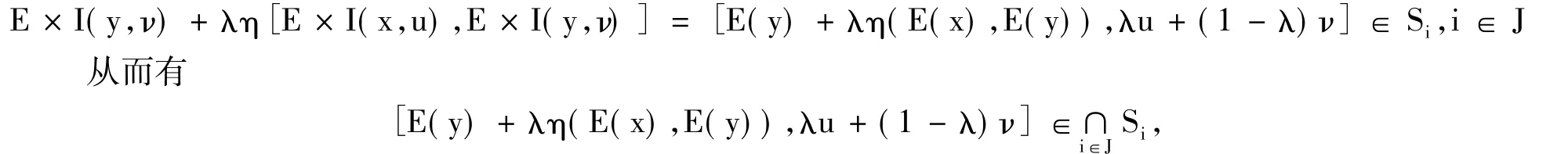
即∩i∈JSi是Rn×F中的E×I-不變凸集.

定理5 設S為E-不變凸集，則F為S上的半E-預不變凸模糊數值函數當且僅當

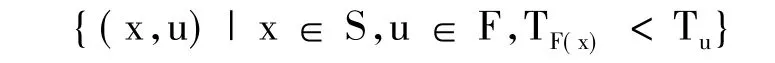
是Rn×F中的E×I-不變凸集.

于是由定理2有，F為S上的半E-預不變凸模糊數值函數當且僅當S(F)是Rn×F中的E×I-不變凸集.

現在定義F在S上的epigraph為：

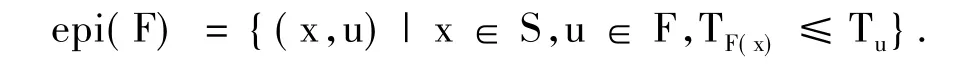
定理6 設S為E-不變凸集，則F為S上的半E-預不變凸模糊數值函數當且僅當epi(F)是Rn×F中的E×F-不變凸集.

證明 設F為S上的半E-預不變凸模糊數值函數，對任意的(x，u)，(y，ν)∈epi(F)及λ∈［0，1］，有

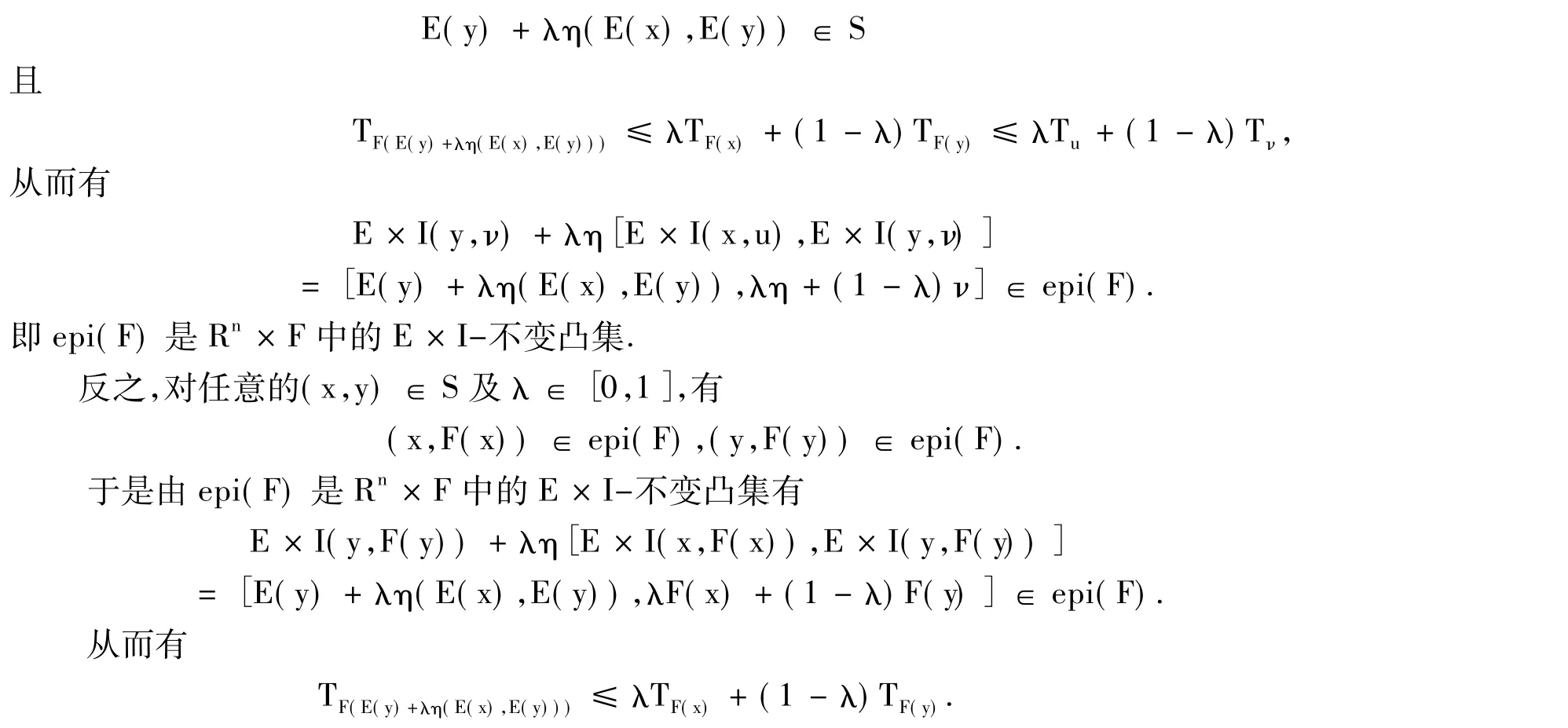
即F是S上的半E-預不變凸模糊數值函數.

定理7 設{Fi|i∈J}是一族S上的半E-預不變凸模糊數值函數，若對任意的x∈S，sup{Fi(x)|i∈J}在F中都存在，則F(x)=sup{Fi(x)|i∈J}是S上的半E-預不變凸模糊數值函數.

證明 對任意i∈J，{Fi}都是S上的半E-預不變凸模糊數值函數，從而由定理6有

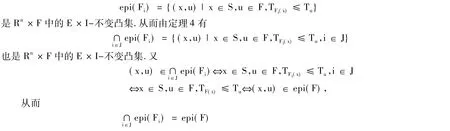
也是Rn×F中的E×I-不變凸集.由定理6有，F是S上的半E-預不變凸模糊數值函數.

定理8 設Fi∶S→F(i=1，2，…，k)對同一個映射E∶Rn→Rn在S上都是半E-預不變凸模糊數值函數，則

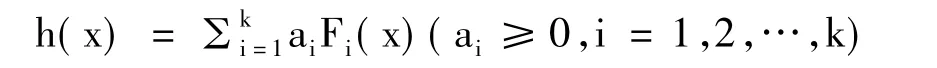
也是S上的半E-預不變凸模糊數值函數.

證明 因為Fi∶S→F(i=1，2，…，k)對同一個映射E∶Rn→Rn在S上都是半E-預不變凸模糊數值函數，即對任意的x，y∈S及λ∈［0，1］有

即h是S上的半E-預不變凸模糊數值函數.

定理9 設F∶S→F為S上的半E-預不變凸模糊數值函數，則

(1)當?∶F→F為非降凸映射時，復合函數?oF∶S→F是S上的半E-預不變凸模糊數值函數;

(2)當?∶F→F為正齊非降次可加映射時，復合函數?oF∶S→F是S上的半E-預不變凸模糊數值函數.

證明 對任意的x，y∈S及 λ∈［0，1］，有

即?oF∶S→F是S上的半E-預不變凸模糊數值的函數.

［1］Nanda S，Kar K.Convex fuzzy mappings［J］.Fuzzy Sets adnd Systems，1992，48：129-132.

［2］Syau Y.R.Generalzation of preinvex and B-vex fuzzy mappings［J］.Fuzzy Sets and Systems，2001，120：533-542.

［3］Panigrahi M.Convex fuzzy mapping with differentiability and its application in fuzzy optimization［J］.European Journal of Operational Research，2007，185：47-62.

［4］Noor M.A.Fuzzy preinvex functions［J］.Fuzzy Sets and Systems，1994，64：95-104.

［5］Youness E.A.E-convex sets，E-convex functions，and E-convex programming［J］.Journal of Optimization Theory and Applications，1999，102：439-450.

［6］吳從，馬明.模糊分析學基礎［M］.北京：國防工業出版社，1991.

［7］R.Goetschel Jr.W Voxman.Elementary fuzzy calculus［J］.Fuzzy Sets and Systems，1986，18：31-43.

［8］Syau Y.R，Lee E.S.Some Properties of E-convex Functions［J］.Applied Mathematics Letters，2005，18：1074-1080.

［9］Syau Y.R，Lee E.S.Stanley Generalizations of E-conves amd B-vex functions［J］.Computers and Mathematics with Applications，2009，58：711-716.

［10］YANG Xinin.On E-convex sets，E-convex functions and E-convex programming［J］.J.Optimi.Thory.Appl，2001，109：699-704.

［11］Fulga C，Preda V.Nonlinear programming with E-preinvex and local E-preinvex functions［J］.European Journal of Operational Research，2009，192：737-743.

［12］李紅霞，鞏增秦.模糊數值函數的凸性與可導性［J］.西北師范大學學報(自然科學版)，2007，43(5)：1-7.

［13］鞏增泰，白玉娟.預不變凸模糊數值函數及其應用［J］.西北師范大學學報(自然科學版)，2010，46(1)：1-5.