玻色—愛因斯坦凝聚現象中幾個問題的探討

潘營利

(渭南師范學院物理與電氣工程學院，陜西渭南714000)

玻色—愛因斯坦凝聚現象是玻色統計中的一種重要現象，許多文獻［1－4］都從不同角度對此做了闡述，但對其量子相變過程則討論得較少.本文以理想玻色—愛因斯坦氣體為例，從量子統計出發，對量子相變過程中的幾個問題作以全面探討，旨在使人們對此有一個全面的認識.

1 相變點方程及相變點曲線

對于理想玻色—愛因斯坦氣體，由玻色統計有［5］：

此即為用P，V表示的相變點方程，由該方程可得相變點曲線如圖1所示.

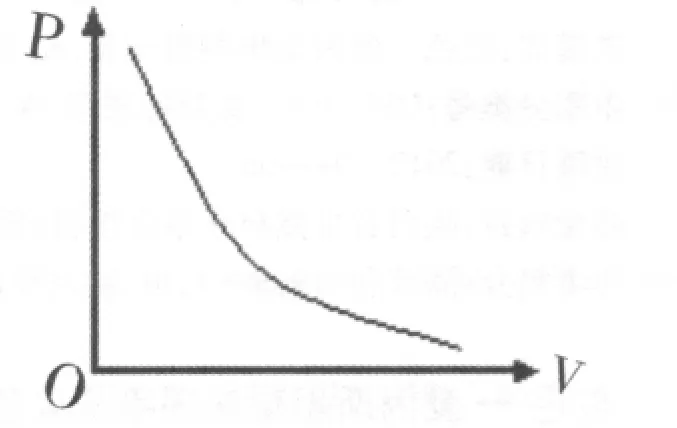
圖1 玻色—愛因斯坦氣體相變點曲線

應該注意，玻色—愛因斯坦氣體出現凝聚相意味著不穩定發生，這一點利用穩定性判據即可看出［6］.在T＞TC時，凝聚相的粒子數為零，故

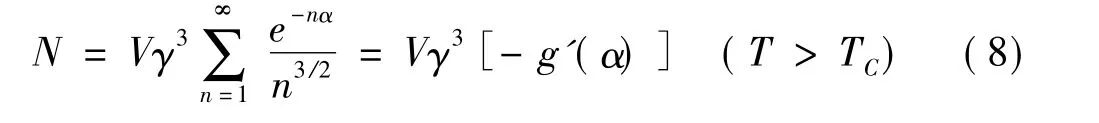
在T，V不變的條件下把(8)式對化學勢μ求導數，注意到μ=－ kTα，則有

這是臨界態的條件.由穩定性判據知，若這個態是穩定的，還要求=0.由于求導是在V不變下進行的，故求可換為求.同理(9) 式可寫為

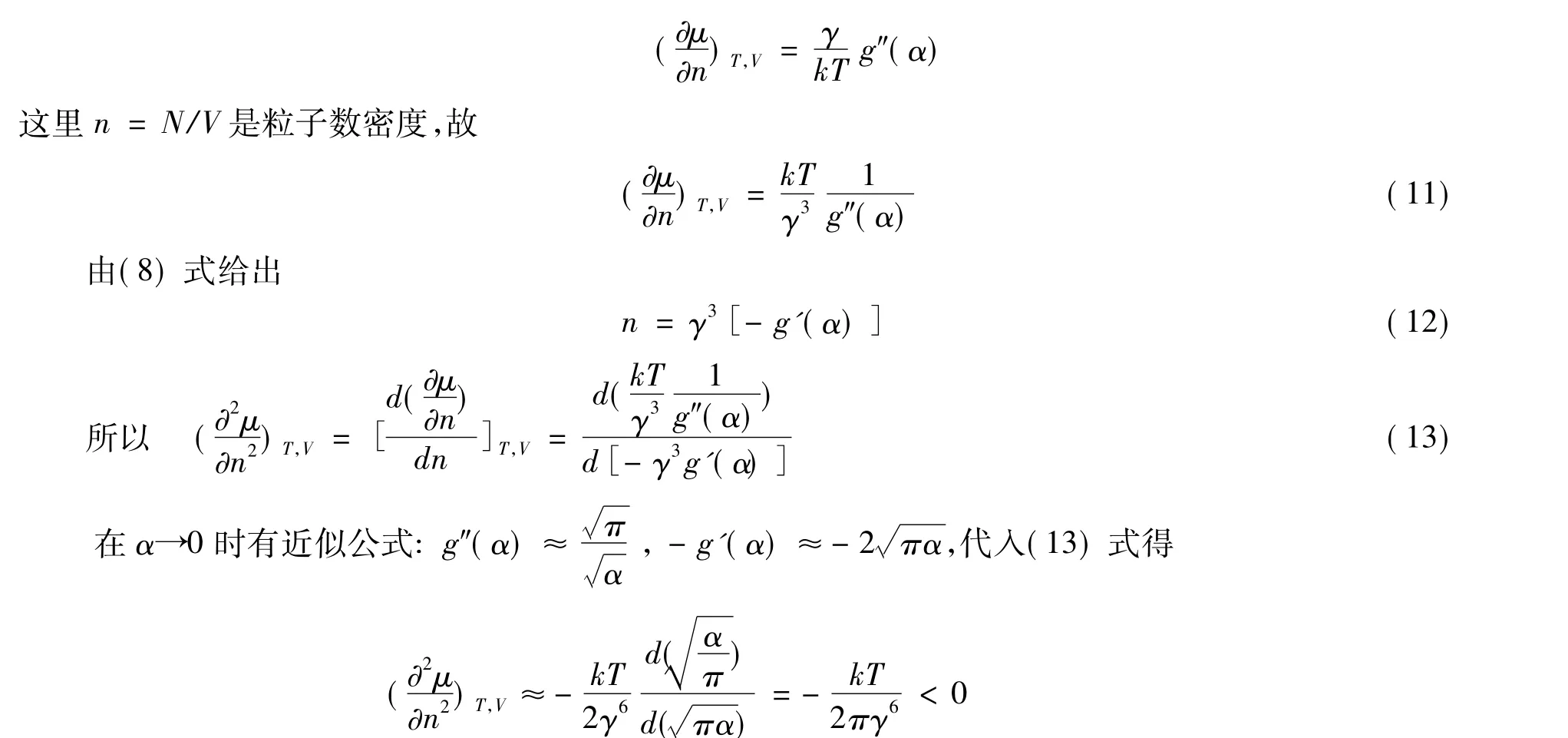
因此，這個臨界態是不穩定的，要發生相的分離.

2 等溫線方程及等溫線

對于玻色—愛因斯坦氣體，當T ＞TC時，μ≠0，α≠0;當T ＜TC時，μ=0，α=0，所以，其等溫線方程在T＞TC和T＜TC時會表現出不同的形式.

2.1 T ＞ TC時

此時壓強和粒子數滿足關系式(2)和(3)，(3)/(2)得：

(14)式即為T＞TC時玻色—愛因斯坦氣體的物態方程，當T一定時，即為T＞TC時的等溫線方程，其α值可由(2)確定，且α僅依賴于溫度T.

2.2 T ＜ TC時

此時，α→0，由于凝聚現象的發生，(2)式不再成立，其(3)式變為：

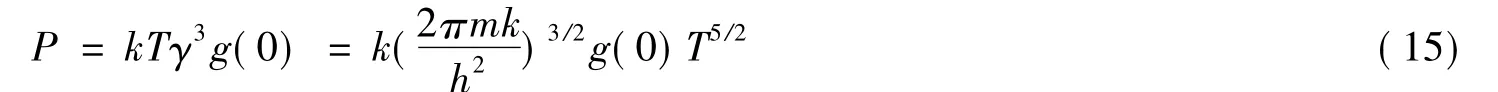
(15)式即為T＜TC時玻色—愛因斯坦氣體的物態方程，可以看出，此壓強只依賴于溫度，與體積無關，并隨T→0而趨于零.當T一定時，即為T＜TC時的等溫線方程.可以證明，當T=TC時，(14)式和(15)式趨于一致.

綜合以上討論可得玻色—愛因斯坦氣體的等溫線方程為：

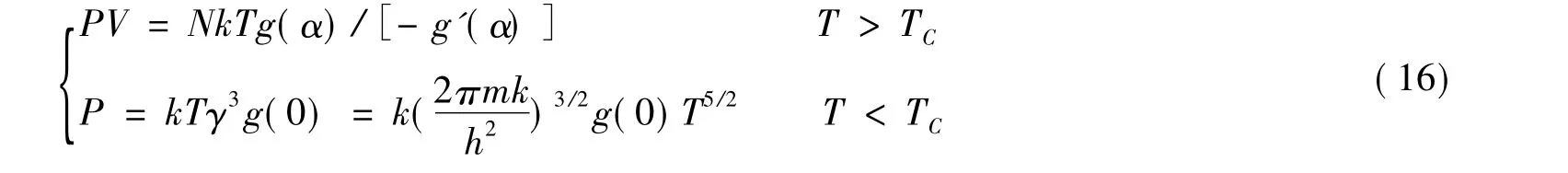
其等溫線如圖2所示.可見，等溫線在T=TC處是連續的，是一條連續的曲線.

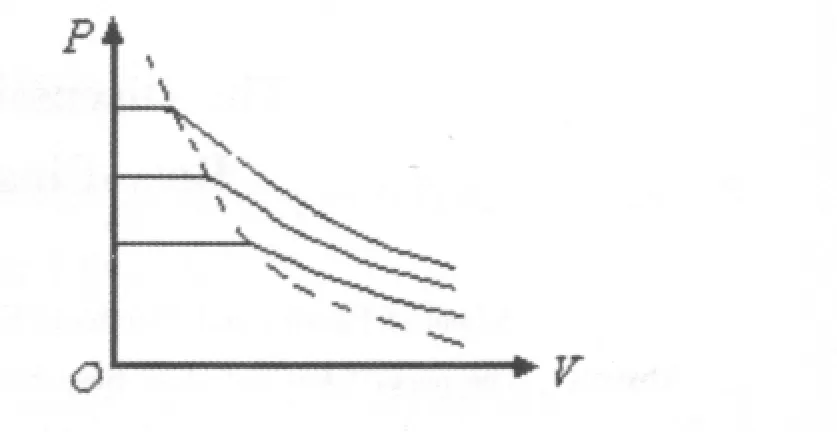
圖2 玻色—愛因斯坦氣體等溫線(實線為等溫線，虛線為相變點曲線)

3 兩相平衡共存曲線方程和兩相平衡共存曲線

兩相平衡共存時，有μ1(T，P)= μ2(T，P)，從理論上講，由 μ1(T，P)= μ2(T，P) 可給出兩相平衡共存曲線.由于凝聚相的μ2(T，P)=0，故由兩相平衡共存條件得：

同理，由 S=k(lnΞ + αN+ βU) 及(1)、(2)、(17)、(18)式可得摩爾熵為：

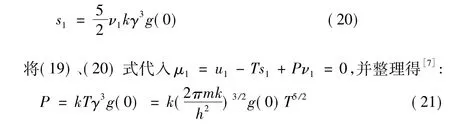
(21)式即為兩相平衡共存曲線方程，由于兩相共存時T≤TC，所以，兩相平衡共存曲線有一個終點;同時可以看出，利用量子統計理論可以給出兩相平衡共存曲線所滿足的方程.由兩相平衡共存曲線方程可給出兩相平衡共存曲線如圖3所示.

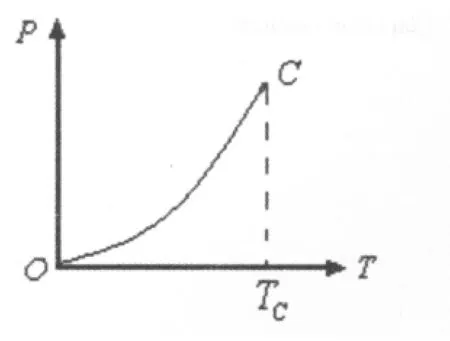
圖3 兩相平衡共存曲線

4 克勞修斯—克拉伯龍方程

克勞修斯—克拉伯龍方程描述的是兩相平衡共存曲線的斜率所滿足的方程.由(21)式可得：

(22)式即為玻色—愛因斯坦氣體的克勞修斯—克拉伯龍方程.對于該方程，也可由兩相平衡共存條件來得到.由(17) 式得：dμ1=0，而 dμ1= － s1dT+ ν1dP，所以

將(20)式代入(23)式即可得(22)式.

值得注意的是，這里所說的相變是在推廣的意義上來理解的，因為這里的相變不是發生在真實空間，而是發生在動量空間里，因此，有些概念的理解不能完全和真實空間的相變過程一樣理解.

以上我們對玻色—愛因斯坦凝聚現象中的幾個問題作了全面的說明，了解這些對于全面掌握玻色—愛因斯坦凝聚現象是非常有用的.

［1］余學才，莫影.勢場中玻色—愛因斯坦凝聚的臨界溫度［J］.物理學報，2004，53(12)：4075－4080.

［2］李紅，林振權.重力場中相對論玻色氣體的凝聚［J］.曲阜師范大學學報(自然科學版)，2011，37(3)：58－61.

［3］余學才，葉玉堂，程琳.勢阱中玻色—愛因斯坦凝聚氣體的勢場有效性和粒子數極限判據［J］.物理學報，2006，55(2)：551－554.

［4］劉澤專，楊志安.噪聲對雙勢阱玻色—愛因斯坦凝聚體系自俘獲現象的影響［J］.物理學報，2007，56(3)：1245－1251.

［5］汪志誠.熱力學統計物理［M］.第3版.北京：高等教育出版社，2003.293.

［6］龔昌德.熱力學統計物理學［M］.北京：人民教育出版社，1982.241，243.

［7］［美］L.E.雷克.統計物理現代教程［M］.北京：北京大學出版社，1983.291，338.