中國國債利率期限結構動態估計及預測

賀暢達，齊佩金，王志強

(東北財經大學 a.應用金融研究中心;b.金融學院，遼寧 大連 116025)

一、引 言

傳統的利率期限結構估計主要從兩個方面進行:一方面是依據經濟理論推導得出，包括均衡模型(或稱為仿射模型)和無套利模型;另一方面是利用統計方法對利率曲線進行擬合，再通過參數的變化過程來預測未來的利率期限結構。均衡模型以不同到期期限的利率基于短期瞬時利率為條件，假設風險溢價服從某種形式隨機過程(一般采用仿射函數形式)，求解債券價格滿足的隨機微分方程的參數，得到利率期限結構模型。主要包括Merton模型［1］、Vasicek模型［2］和一般均衡 CIR 模型［3］等。Duffie等(1996)［4］則證明了上述均衡模型都屬于一類仿射模型。無套利模型假設不同到期期限的利率之間不存在套利機會，通過風險中性求解債券價格校準利率期限結構模型。HJM模型［5］是無套利模型的一般框架。均衡模型可以用來為債券及其衍生物進行定價，屬于傳統的動態模型，但是Duffee(2002)［6］的研究認為仿射模型的樣本外預測能力甚至不如隨機游走過程對利率期限結構動態的預測。無套利模型則更關注利率期限結構的橫截面的擬合，而非縱列的時間序列對利率的預測。

統計模型包括靜態模型和混合動態模型。靜態估計主要是構建貼現函數，而后通過貼現率與即期利率關系擬合利率期限結構。McCulloch(1971)［7］、Vasicek等(1982)［8］分別利用多項式樣條法和指數樣條法來估計利率期限結構。Nelson等(1987)［9］構建三因子的簡約模型，NS模型對利率曲線的擬合能力強，因而在實務中得到了廣泛的應用。Svensson(1994)［10］推導出四因子的NS模型的擴展形式，提高了NS模型的擬合精度。然而，這些靜態模型只能擬合某一時點的利率曲線，不能描述利率曲線的動態變化，也不能對未來進行預測。Diebold等(2006)［11］結合靜態的NS模型，利用NS模型三因子的動態變化規律來動態估計和預測利率期限結構，因此被稱為動態Nelson-Siegel模型(DNS)或DL模型，屬于混合動態模型。隨后學者利用DNS模型對不同國家的利率期限結構進行估計和預測，發現模型的預測能力遠超過傳統的動態模型，但是DNS模型仍然屬于在統計意義上的建模，缺乏經濟理論的支持。

考慮到均衡模型和無套利模型缺乏對利率期限結構的預測能力，而統計模型又缺乏經濟理論基礎，Christensen 等(2009，2011)［12－13］將屬于統計模型的NS模型與具有經濟理論基礎的無套利和仿射模型相結合，提出了無套利NS模型，包括無套利DNS模型(簡稱AFDNS模型)和廣義無套利NS模型(簡稱AFGNS模型)。這類模型假設短期瞬時利率服從仿射形式，利用無套利約束推導出來具有NS因子形式的模型。經驗結果顯示，AFDNS模型的樣本內估計與樣本外預測能力都較強，AFGNS模型對樣本內利率期限結構的動態擬合度高。

近幾年，國內學者也采用多種方法來估計以及預測中國的利率期限結構。姚長輝等(1998)［14］用回歸插補法和三次樣條插值法構造國債到期收益率曲線。朱世武等(2003)［15］運用 Nelson-Siegel模型和Nelson-Siegel-Svensson模型對我國利率期限結構進行估計，他們認為Nelson-Siegel-Svensson模型的近端擬合效果好，但遠端擬合不夠靈活。范龍振等(2005)［16］利用卡爾曼濾波法，以及仿射模型和廣義高斯仿射模型對上交所利率期限結構進行估計和預測，實證研究結果表明，廣義高斯仿射模型的樣本內估計與樣本外預測效果更好。宋福鐵等(2006)［17］利用CIR模型，采用卡爾曼濾波法估計和預測上交所的國債期限結構。葉振軍等(2009)［18］構建時變參數的NS模型，利用主微分方法對滬市國債利率期限結構進行估計和預測等分析。康書隆等(2010)［19］以及康書隆(2010)［20］利用面板數據兩步法對DNS模型進行估計，并且與樣條法的擬合精度進行對比，發現DNS模型具有較大優勢。余文龍等(2010)［21］利用銀行間國債數據，考察卡爾曼濾波法對DNS模型的樣本內估計能力，并比較DNS模型與隨機游走、主成分預測等方法對利率期限結構的預測能力，研究發現DNS模型的樣本內估計和樣本外預測能力都較強。

但是，到目前還沒有學者利用AFGNS模型對中國利率期限結構進行估計，不知道與傳統動態模型相比該模型的解釋能力和預測能力是否具有優勢。有鑒于此，本文利用AFGNS模型對我國的國債利率期限結構進行估計，與其他學者利用傳統模型對利率期限結構的估計結果進行比較，考察該模型對我國利率期限結構動態變化的樣本內解釋能力和樣本外預測能力。

二、模型構建

Christensen等(2009)［12］的研究證明在無套利約束下，在風險中性Q-測度下，從仿射形式短期瞬時利率，可以推導出具有NS模型的五因子擴展形式的AFGNS模型。對美國國債利率期限結構的動態估計經驗結果表明:AFGNS模型對樣本內的動態估計能力強于DNS等模型，說明AFGNS模型能夠較好地刻畫利率期限結構動態變化特征，但是他們的研究并沒有對AFGNS模型的樣本外預測能力進行檢驗。本文采用AFGNS來估計和預測我國國債的利率期限結構。AFGNS模型可以表示為信號方程

(1)式和狀態方程(2)式組成的狀態空間形式:

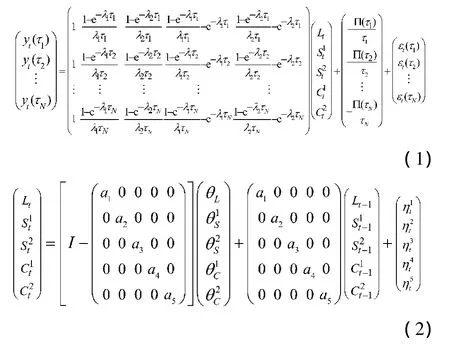
式中，yt(τ)表示t時刻到期期限為τ的零息債券利率，五個因子的狀態變量分別表示水平、兩個斜率和兩個曲度因子。在風險中性Q-測度下五因子的動態變化過程服從式(2)，－Π(τ)/τ是模型的無套利調整項，λ1和 λ2分別代表不同的指數衰減率。五因子模型可以擬合出駝峰、雙峰等有兩極值點的曲線，這都是三因子模型所不能的。因此，這個模型會大大增加利率曲線擬合時的靈活性，更接近實際利率曲線的形態，而且這種形式在理論的推導及證明時易于引入無套利條件。

三、實證分析

1.數據

本文選用2002年1月至2012年6月銀行間債券市場的國債交易月度數據(剔除異常價格的債券)作為本文的樣本數據，所有數據都來自Wind資訊和中債信息網。首先，用Fama-Bliss方法［22］從國債價格中剝離得到離散的即期利率作為模型估計的先驗數據［19］，得到 Fama-Bliss樣本數據后，再將數據分為兩部分:第一個子樣本從2002年1月至2009年12月，用來估計參數做樣本內擬合;第二個子樣本區間為2010年1月至2012年6月，作為利用第一個子樣本得到的參數進行模型的樣本外預測的基準數據。

2.模型參數估計與樣本內誤差

利用Kalman濾波法對表示成狀態空間形式的AFGNS模型進行參數估計，得到模型參數估計值(見表1)。AFGNS模型有兩對斜率與曲率因子，也有對應的兩個指數衰減率λ1和λ2，估計值分別是1.8796和0.2343，分別對應曲率極值出現的位置0.9年和 7.9 年。

表1 AFGNS模型參數估計結果

利用估計AFGNS模型得到的參數進行Kalman平滑，確定狀態因子的動態過程，用來考察AFGNS模型對到期期限從1年到10年的利率期限結構樣本內擬合能力。利用平均誤差、平均絕對誤差MAE、均方根誤差RMSE等三個指標判斷模型的擬合優度。表2為AFGNS模型樣本內擬合度判別的誤差統計。

表2 AFGNS模型樣本內擬合度判別的誤差統計 BP

表2中數據顯示，AFGNS模型樣本內擬合的平均誤差均不到1 BP，平均絕對誤差也都小于26 BP，均方根誤差都在40 BP以內。康書隆等(2010)［19－20］的研究顯示，三次樣條法的平均誤差都在20 BP以上，非線性方法估計NS的平均誤差基本大于100 BP，利用面板數據兩步法估計動態NS模型的平均誤差除了短期外都在10 BP以下。通過比較可以看出，統計模型和DNS模型的擬合優度較三次樣條的擬合優度高，但都低于本文采用的AFGNS模型。另外，范龍振等(2005)［16］采用的仿射模型(均衡模型)及其擴展形式對樣本內擬合的平均誤差多在20 BP左右;宋福鐵等(2006)［17］采用Kalman濾波估計多因素(從1因素到5因素)的CIR模型，所有模型在不同期限的均方根誤差RMSE均在50 BP以上，這都表明AFGNS模型較傳統的理論模型的樣本內擬合也具有優勢。

3.利率期限結構預測

利用第一個子樣本的數據進行參數估計，再利用Kalman預測法對AFGNS模型進行樣本外預測，以第二個子樣本的數據作為樣本外預測的參照數據，判斷模型的預測能力。由于數據為月數據，因此選取向前1，6，12步的預測，即是對未來1個月、6個月和12個月的到期期限為1到10年的利率期限結構的預測。通過預測的平均絕對誤差FMAE和預測的均方根誤差FRMSE等指標來評價AFGNS模型的樣本外預測能力。

表3列出利用AFGNS模型進行樣本外數據預測的誤差指標。

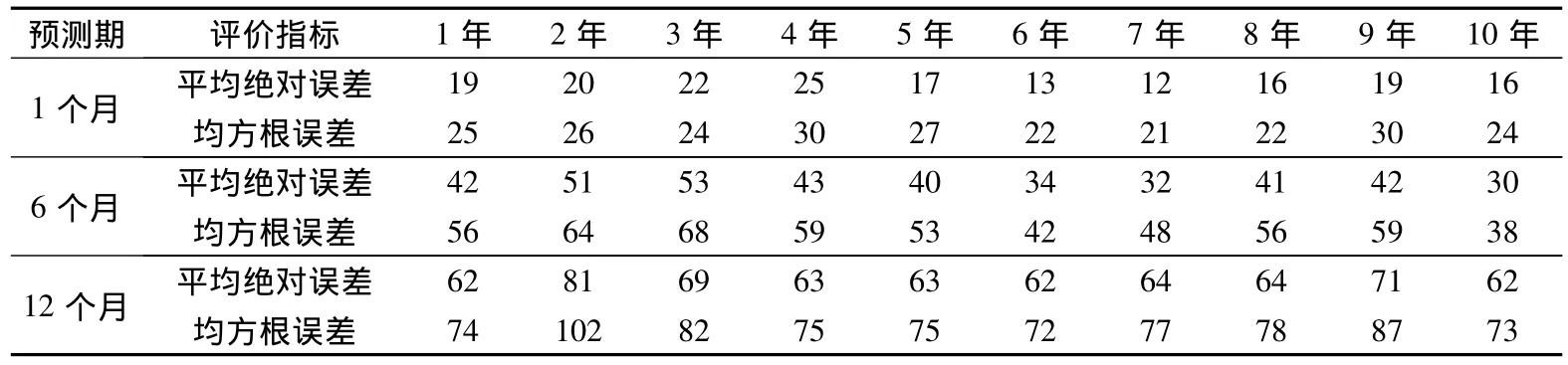
表3 AFGNS模型樣本外預測的誤差統計 BP

通過與其他研究中對利率期限結構的預測來判斷模型的預測效力。國內學者利用傳統模型對未來我國的國債利率期限結構進行預測的研究較少，因為傳統的仿射模型的預測能力較差，如 Duffee(2002)［6］的研究證實均衡模型的預測能力甚至弱于隨機游走模型，而且靜態模型和無套利模型又不具備時間序列上的預測能力。因此，近年來利用DNS模型對利率期限結構進行預測成為利率預測的主要方法。余文龍等(2010)［21］比較了隨機游走模型(比照隨機游走模型的預測能力就可以判斷相應的模型與仿射模型的預測能力)、斜率預測、遠期利率預測和主成分預測方法與DNS模型的樣本外預測能力，經驗研究結果表明DNS模型短期預測效果與其他模型差別不大，但DNS模型表現出較強的長期預測能力。其中，對于1個月的預測，各模型的均方根誤差均在20 BP到30 BP之間，各模型的預測能力相當，與本文采用的AFGNS模型的預測能力基本持平;對于6個月的預測，DNS模型的均方根誤差在70 BP以上，其他模型都在80 BP以上，本文的AFGNS模型的預測誤差則都小于70 BP;對未來12個月的預測中，DNS的預測均方根誤差位于80 BP到110 BP之間，其他模型都在100 BP以上，而本文的AFGNS模型的預測均方根誤差基本位于70 BP到100 BP之間。類似地，利用預測的平均絕對誤差FMAE的比較也可以得到AFGNS模型在較長期預測方面優于其他傳統模型。

綜上，可以看出AFGNS模型的預測能力在短期的優勢不明顯，但對于多步較長期預測的能力較強，優于傳統模型以及DNS模型。

四、結 論

本文利用結合無套利理論基礎與NS模型數據擬合優勢的AFGNS模型，對我國銀行間債券市場的國債利率期限結構進行動態估計和預測。對比康書隆等(2010)［19－20］、范龍振等(2005)［16］以及宋福鐵等(2006)［17］利用靜態模型(三次樣條法)、傳統動態模型(多因子CIR仿射模型)和混合動態模型(DNS模型)對我國的國債利率期限結構曲線的擬合能力和樣本內動態估計能力，AFGNS模型由于加入兩對斜率與曲率因子，可以描述利率曲線變化的多峰形態，因此可以更好地擬合利率期限結構。還利用AFGNS模型進行樣本外預測，并與余文龍等(2010)［21］得出的隨機游走模型、斜率預測和 DNS模型等方法的樣本外預測能力進行對比，結果發現AFGNS模型的短期預測能力與其他模型相近，但對于長期預測，AFGNS模型則顯示出較大的優勢。這一方面是由于五因子的加入使得模型可以對利率曲線進行更精確的擬合，另一方面無套利約束的加入也提高了模型的預測能力。因此，通過實證研究以及與其他模型的比較，本文所采用的廣義無套利NS模型的動態估計效率優于傳統模型以及被廣泛使用的DNS模型，可以為進一步的微觀金融及宏觀金融的研究提供基礎參考模型。

［1］MERTON R.An intertemporal capital asset pricing model［J］.Econometrica，1973，41(5):867－887.

［2］VASICEK O.An equilibrium characterization of the term structure［J］.Journal of Financial Economics，1975，5(2):177－188.

［3］COX J，INGERSOLL J，ROSS S.A theory of the term structure of interest rates［J］.Econometrica，1985，53(2):85－407.

［4］DUFFIE D，KAN R.A yield-factor model of interest rates［J］.Mathematical Finance，1996，6(4):379－406.

［5］HEATH D，JARROW R，MORTON A.Bond pricing and the term structure of interest rates:a new methodology for contingent claims valuation［J］.Econometrica，1992，60(1):77－105.

［6］DUFFEE GR.Term premia and interest rate forecasts in affine models［J］.Journal of Finance，2002，57(1):405 －443.

［7］MCCULLOCH H.Measuring the term structure of interest rates［J］.Journal of Business，1971，44(1):19 －31.

［8］VASICEK A，FONG G.Term structure modeling using exponential splines［J］.Journal of Finance，1982，37(2):339－348.

［9］NELSON R，SIEGEL F.Parsimonious modeling of yield curves［J］.Journal of Business，1987，60(4):473 －489.

［10］SVENSSON O.Estimating and interpreting forward interest rates:Sweden 1992 －1994［J］.IMF Working Papers 94/114，International Monetary Fund，1994.

［11］DIEBOLD X，LI C.Forecasting the term structure of government bond yields［J］.Journal of Econometrics，2006，130(2):337－364.

［12］CHRISTENSEN H，DIEBOLD X，RUDEBUSCH D.An arbitrage-free generalized Nelson-Siegel term structure model［J］.The Econometrics Journal，2009，12(3):33 －64.

［13］CHRISTENSEN H，DIEBOLD X，RUDEBUSCH D.The affine arbitrage-free class of Nelson-Siegel term structure models［J］.Journal of Econometrics，2011，164(1):4 －20.

［14］姚長輝，梁躍軍.我國國債收益率曲線的實證研究［J］.金融研究，1998(8):12－18.

［15］朱世武，陳健恒.交易所國債利率期限結構實證研究［J］.金融研究，2003(10):63 －73.

［16］范龍振，張國慶.仿射模型、廣義仿射模型與上交所利率期限結構［J］.管理工程學報，2005(3):97－101.

［17］宋福鐵，陳浪南.卡爾曼濾波法模擬和預測滬市國債期限結構［J］.管理科學，2006(6):81－88.

［18］葉振軍，張慶翠，王春峰.時變參數NS期限結構模型的主微分分析及其實證研究［J］.預測，2009(4):62－65.

［19］康書隆，王志強.中國國債利率期限結構的風險特征及其內含信息研究［J］.世界經濟，2010(7):121－143.

［20］康書隆.中國國債利率期限結構估計——基于面板數據的兩步法［J］.財經問題研究，2010(6):62－67.

［21］余文龍，王安興.基于動態Nelson-Siegel模型的國債管理策略分析［J］.經濟學(季刊)，2010(4):1403 －1426.

［22］FAMA F，BLISSR.The information in long-maturity forward rates［J］.American Economic Review，1987，77(4):680－692.