形變分析中的模型精化研究

胡杰

(廣東省電力設計研究院，廣東廣州 510663)

1 前言

現代測量數據處理中，影響觀測值取值的因素很多，大概分為兩部分:一部分為已知函數部分，作為參數分量;另一部分為某些干擾因素，同觀測量的關系是完全未知的，可以將其看作非參數分量，即用非參數分量表達參數模型表達不完善的部分。

在我們建立數學模型時往往無法考慮到所有因素。為處理方便，常選擇較為簡單的函數來代替。因此，平差建立的函數模型只是實際的近似描述，即存在模型誤差。當模型誤差與偶然誤差相比是一個微小量時，可以忽略模型誤差。而當模型誤差較大時，就會對參數估值產生較大影響，甚至會產生錯誤結論［2］。

本文詳細分析兩種將參數和非參數模型進行組合的混合模型算法，即“基于時間序列的半參數回歸分析法”和“基于線性回歸的神經網絡精化法”。

2 參數模型和非參數模型

參數回歸模型對回歸函數提供大量信息，當假設的模型成立時，未知數解具有較高精度。但由于回歸函數的形式假設是已知的，只是參數待定，所以回歸形式一旦固定就相對呆板，往往回歸效果差。非參數回歸與參數回歸則正好相反，它的回歸函數形式是任意的，不拘束于觀測量的分布限制，具有很強的適應性。但實際上對擬合函數不作任何限制是不可能的，在非參數回歸方法中，無論最近鄰法、核函數法、樣條函數法都存在參數選擇的問題，這也是非參數回歸模型的難點。

2.1 參數回歸模型

假設對(L，X)作 n 次等精度觀測(Li，Xi)，i=1，2，…，n，則有:

式中:B為列滿秩矩陣;X為參數向量;△為隨機誤差項。

2.2 非參數回歸模型

參數模型中，觀測值是未知參數的線性函數，從而要求數據處理中提供大量額外信息，由于參數模型的局限性，數學界提出了非參數模型，如下所示。

假設(Yi，Xi)，i=1，2，…，n，滿足:

{εi}服從 E(εi)=0獨立同分布，{Xi}可以是隨機的或非隨機。一般情況下，只考慮非隨機的情況，也就是說，回歸函數g(X)的估計n(X)總可以表示為如下形式:

在一般實際問題中，權函數滿足下述條件:

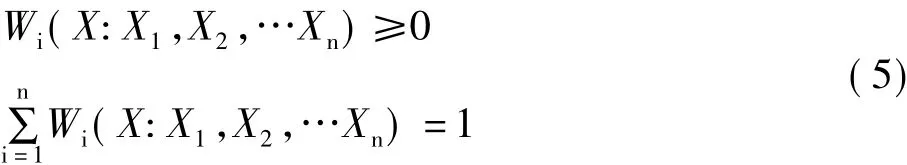
滿足上述條件的權函數為概率權。不同的權函數形式產生了不同的估計方法。由于對y=g(x)的具體形式沒有作任何假設，這個模型比參數模型具有更大的適應性。然而非參數模型無法利用經驗或試驗資料提供的這些信息，明顯降低了模型的解釋能力。

3 組合模型

通過以上分析，我們考慮如何兼顧參數模型和非參數模型的優點，對現有數據分析模型進一步精化，從而較單純的參數模型或非參數模型有更大的適應性，并具有更強的解釋力，更接近于真實。接下來就詳細介紹兩種精化模型，即“基于時間序列的半參數回歸分析法”和“基于線性回歸的神經網絡精化法”。

3.1 基于時間序列的半參數回歸分析法

半參數回歸模型由參數部分和非參數部分共同組成，在測量中的應用處于探索的階段，目前主要是通過構造正規化矩陣和平滑參數，利用補償最小二乘法獲取參數和非參數解。

在半參數模型中，平滑參數主要利用交叉核實法確定。由于變形觀測值是以一定的時間序列為基礎，若假設相鄰時刻的模型誤差si與si+1的差別不應太大。因此可令，此時可以選擇如下形式的正則化矩陣:

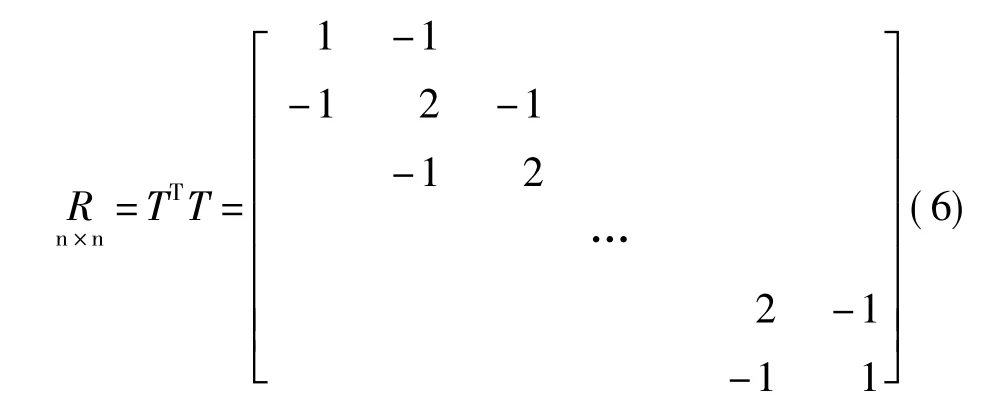
這時因rank(R)=n－1＜n，即R秩虧，還需再增加一個約束條件。若進一步假設S呈周期性變化，觀測值分布均勻，個數足夠，則可令，增加這一約束條件可以解決秩虧的問題。利用時間序列法由上式選擇的正則化矩陣R，在實踐中得到了較為廣泛的應用。

于是平差問題歸結為下述條件極值問題:

同樣來構造拉格朗日函數:

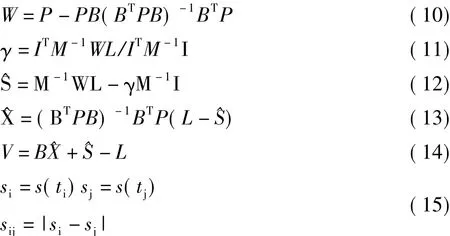
3.2 基于線性回歸的神經網絡精化法

在形變分析中，我們可以把變形序列看成由趨勢項、周期項和觀測誤差三部分組成。趨勢項利用經典最小二乘法求解。其他部分可以利用神經網絡去映射。神經網絡算法強大的自學習功能，在模型精化過程中，既彌補前述精化模型的不足，又沒有人為假設所產生的誤差，在理論上這樣能得到較好的效果［7］。

3.2.1 基于神經網絡的精化模型

變形觀測的每期數據屬于獨立觀測值，所以可以看作等精度觀測值來討論函數模型的精化方法。精化模型為:

式中:A為列滿秩矩陣;X為參數向量;G為模型的精化部分;△為隨機誤差項。

在此模型中參數X起解釋模型物理意義的作用，而G起對趨勢模型修正的作用。實質上G也是參數X和觀測值L的函數，即

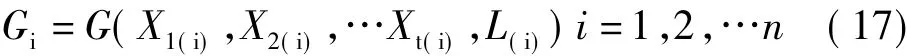
只是它們之間的關系是隱含的，通過神經網絡得到它的顯式數值表示。這樣利用神經網絡使得式(16)的模型既具有物理意義，又達到比較理想的精度。

3.2.2 參數X的估計

利用變形觀測的n次觀測數據，選定根據實際問題所采用的線性回歸模型，在最小二乘準則下，可得X最優無偏估計^X為

3.2.3 參數G的估計

基于線性擬合的回歸殘差，利用改進的神經網絡BP算法求解參數G。具體過程為

(1)計算n期變形觀測數據的回歸殘差vi

(2)利用n期變形觀測數據的所有信息構成神經網絡模型:①選定輸入層:由變形觀測值產生影響的因素，設為(X1(i)，X2(i)，…Xt(i))和回歸殘差 vi組合構成;②選定輸出層:參數G;③ 構造迭代模型:在對BP算法進行深入研究的基礎上，提出了誤差分級迭代的改進BP算法，它能有效地提高BP網絡的穩定性。其基本思路為:先將設定的學習誤差ε0進行分級，若將ε0分為n級，則分級公式為:

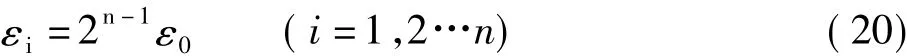
然后依次取εi為收斂控制參數對學習樣本集進行學習訓練，當第n級誤差ε0迭代收斂后，網絡的學習過程結束［6］。

4 工程實例

以某混凝土大壩5#104點2003年1月～2006年12月的垂直位移作為實驗數據，根據原始的觀測資料的水位和溫度數據，共選出48組子樣，其中2003年1月～2005年12月的共36組樣本用來建模，2006年1月～2006年12月的共12組進行預測。為了分析出該大壩的形變規律，分別建立多項式回歸分析模型、基于時間序列的半參數回歸模型和基于線性回歸的神經網絡精化模型，用3個模型進行預報，對預報的結果進行比較。

4.1 回歸模型

回歸模型采用二次多項式模型，其中，xi表示壩前水位，yi表示溫度，利用最小二乘法求解出回歸方程:

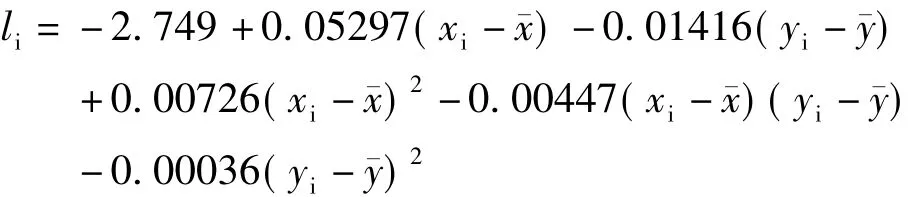
通過計算得二次多項式模型的內符合精度為±0.322 mm，外符合精度為±0.305 mm。

4.2 基于時間序列的半參數回歸分析模型

建立半參數模型的關鍵是構造平滑參數和正規化矩陣。平滑參數利用交叉核實法確定為α=0.21，因為變形分析的觀測數據具有時序性，所以選取基于時間序列的正規化矩陣，建立時間序列半參數回歸分析模型。

為了分析平滑參數的選取對半參數擬合結果的影響，選取不同參數進行實驗計算，計算結果如表1所示。

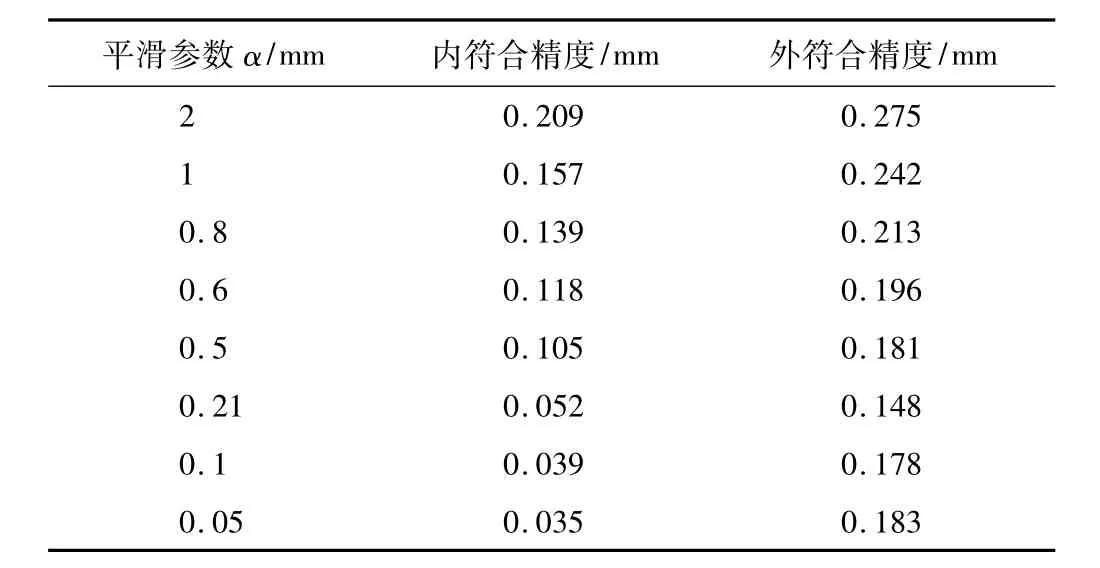
不同平滑參數實驗結果比較 表1

分析結果我們可以看出，對于該工程實例，隨著平滑參數逐漸變小，內符合精度不斷提高，說明該模型的學習能力在不斷提高。同時，根據交叉核實法計算的平滑參數為0.21，外符合精度達到0.148 mm，說明平滑參數的選取基本符合實驗要求，利用交叉核實法確定平滑參數就有一定的可靠性。

4.3 基于線性回歸的神經網絡精化法

采用二次多項式模型為基礎模型，計算二次多項式的回歸殘差。以影響大壩垂直位移的溫度、水位以及回歸殘差vi作為輸入層，設精化值為輸出層，建立基于線性擬合殘差的神經網絡模型。為了分析神經元數目對模型精度的影響，選取不同的神經元數目進行實驗，計算結果如表2所示。

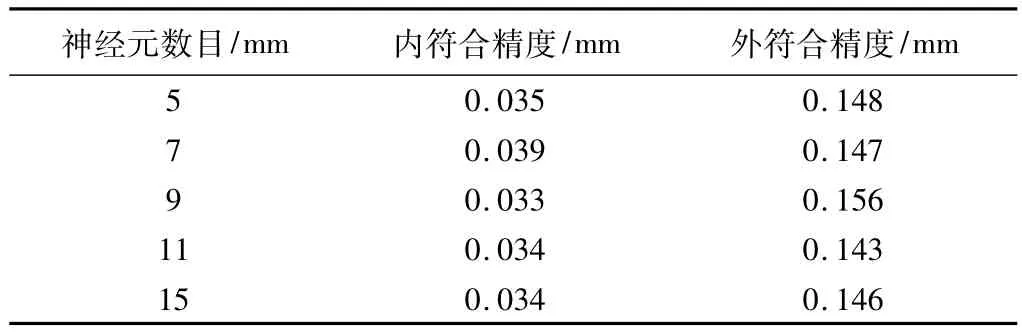
不同神經元實驗結果比較 表2

通過對不同的神經元數目進行實驗分析，我們發現，外符合精度和內符合精度基本保持不變。對于該工程實例，模型具有較高的穩定性。

4.4 不同模型比較

通過以上3個模型的實驗計算，我們選取平滑因子0.21的半參數模型，神經元數目11的神經網絡精化模型以及二次多項式模型與實測值進行比較分析，數據結果如表3所示。

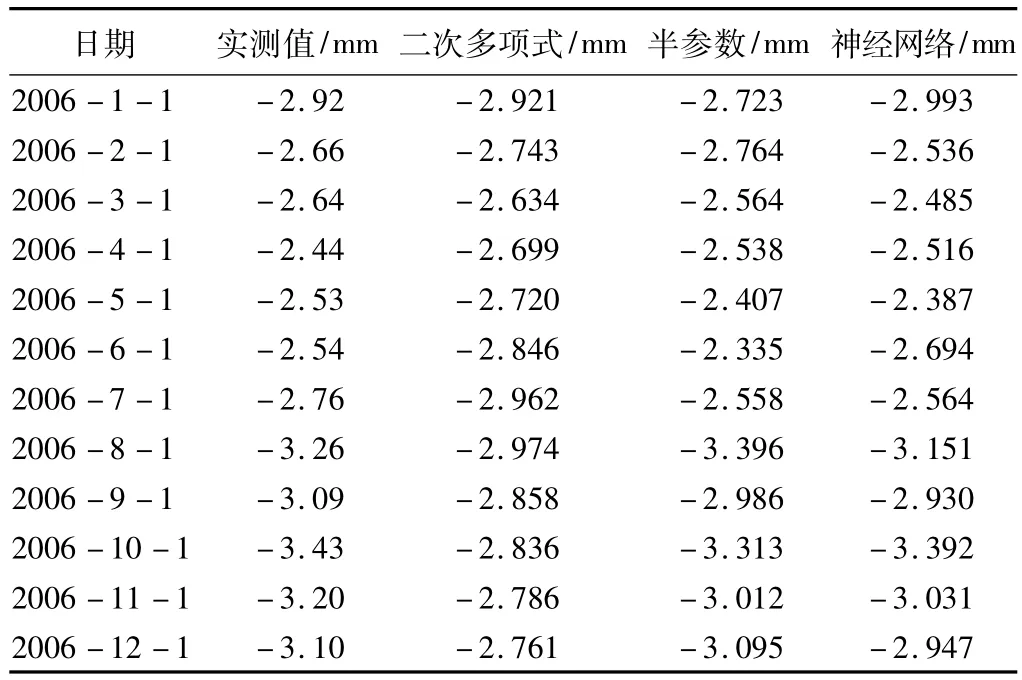
不同模型實驗結果比較 表3

通過實驗，我們可以得到二次多項式的內、外符合精度分別為 ±0.322 mm和 ±0.305 mm，時間序列半參數模型的內、外符合精度分別為 ±0.052 mm和±0.148 mm，基于線性回歸的神經網絡模型的內、外符合精度分別為 ±0.034 mm和 ±0.143 mm。比較發現，相對于簡單的二次多項式模型，后兩種混合體模型無論是在內符合精度，還是在外符合精度上都有很大的提高。而兩種混合體模型相比，神經網絡模型的內符合精度更高，說明其學習能力更強，而在外符合精度上。兩個模型基本相同，說明兩者的預測能力基本相當，都具有很強的預測能力。

5 結論

(1)形變分析的過程中，在利用回歸模型進行擬合時，存在一定的模型誤差，在模型誤差比較大時，會對參數估值產生較大的影響，甚至會導致錯誤的結論。

(2)基于參數和非參數模型優點所構造的混合模型，可以很好的減少常規模型帶來的模型誤差，從而提高計算精度。

(3)形變觀測數據具有時序性，所以選取半參數模型的正規化矩陣時，采用時間序列法，實驗證明取得不錯的效果。通過實驗，我們可以發現平滑參數的選取對半參數的擬合效果也有很大的影響。

(4)采用基于線性回歸的神經網絡精化模型時，以常規模型作為基礎模型，并利用神經網絡算法對回歸殘差進行重新擬合，來修正基礎模型誤差，既克服了單純的神經網絡模型算法所帶來的“黑箱性”，使模型具有相應的物理意義，又提高了模型的計算精度。通過實驗證明，與常規回歸模型相比，效果改善比較明顯。

(5)采用誤差分級迭代模式的改進BP算法，通過實驗，可以發現在保障具有較高預測精度的同時，神經網絡模型學習的效率也有著顯著的提高。

［1］胡伍生.神經網絡理論及其工程應用［M］.北京:測繪出版社，2006.

［2］梁武韜.試驗數據與回歸分析［J］.土木工程學報，2005，38(8):1～5.

［3］丁士俊，陶本藻.半參數模型及其在形變分析中的應用［J］.測繪科學，2004，29(5):38～40.

［4］胡伍生，張志偉.模型誤差補償的神經網絡方法研究［J］.測繪科學，2010，35(S1):47 ～49.

［5］陶本藻.測量數據處理的統計理論和方法［M］.北京:測繪出版社，2007，134 ～192.

［6］胡伍生，沙月進.神經網絡BP算法的誤差分級迭代法［J］.東南大學學報·自然科學版，2003，33(3):376～378.

［7］張志偉，胡伍生，黃曉明.線性回歸模型精化方法［J］.東南大學學報·自然科學版，2009，39(6):1279～1282.

［8］陶本藻，施闖，姚宜斌.顧及系統誤差的平差模型研究［J］.測繪學院學報，2002，19(2):79 ～81.

［9］丁士俊，陶本藻.自然樣條半參數模型與系統誤差估計［J］.武漢大學學報·信息科學版，2004，29(11):964～967.

［10］丁士俊.測量數據的建模與半參數估計［D］.武漢:武漢大學測繪學院，2005.