基于MD－ANP方法的工程項目管理模式評價

胡笑旋， 華 娟

（1.合肥工業大學 管理學院，安徽 合肥 230009；2.合肥工業大學 過程優化與智能決策教育部重點實驗室，安徽 合肥 230009）

0 引 言

工程項目管理模式是為實現工程項目目標而采取的組織和管理方式，是提高項目管理水平的關鍵。事實表明，一個項目靠采用先進的技術方法或設備只能使工程利潤提高3%～5%，而依靠良好的管理方式卻能使工程利潤增加10%～20%［1］。如何科學地評價和正確地選擇工程項目管理模式，對項目的成功至關重要。而工程項目管理模式評價的指標很多，定義的難度大且各指標之間的關系復雜，屬于典型的復雜多準則決策問題（Complex Multiple Criteria Decision Making，簡稱CMCDM）。

文獻［2］提出從組合元素與合同元素2方面對建筑工程項目管理模式進行選擇。

文獻［3］從項目特點、業主需求和業主喜好等3個方面分析，并選擇合適的工程項目管理模式，運用層次分析法（AHP）輔助業主進行決策。

文獻［4］運用區間AHP和粗糙集方法建立了工程項目管理模式的數學評價模式，為業主決策提供依據。

文獻［5］對工程項目管理模式的評價指標進行了Logistics回歸分析。

文獻［6］討論了工程項目管理模式選擇的評價指標，運用模糊AHP方法建立了決策模型，方便業主評價和選擇合適的工程項目管理模式。

文獻 ［7］提出了基于熵權模糊集的建設工程發包模式選擇模型。

文獻［8］針對軍隊建設工程項目，建立了管理模式評價指標體系，并使用模糊層次分析法進行評價。

在評價指標的選取上，以上研究只考慮了內部核心的幾個指標，如項目規模與復雜性特點、項目質量、工期和成本目標等，卻忽略了國家和地方政策的支持度、建筑市場上承包商或咨詢商的能力等外部指標，而這些指標都一定程度上影響工程項目管理模式的選擇。同時，以往多采用AHP方法對工程項目管理模式進行評價，該方法的一個重要前提是評價指標體系必須是內部獨立的遞階層次結構，但是工程項目管理模式的評價指標體系并不滿足這個條件，各指標之間存在一定的相互影響和相互支配關系。

本文使用改進的德爾菲法（Modified Delphi，簡稱 MD）［9－12］確立工程項目管理模式的內外部評價指標，在充分征求和提煉專家意見的基礎上設計評價指標體系。采用網絡分析法（Analytic Network Process，簡稱 ANP）［13－17］構建評價模型，對指標之間的相互支配、相互影響和反饋等關系進行量化描述，并通過對模型的求解實現對多種管理模式的綜合排序。

1 工程項目管理模式評價流程

（1）指標體系的初步構建。對影響工程項目管理模式選擇的元素進行分析，得到指標體系的初步框架。

（2）使用MD方法對指標體系進行確定。MD法的基本思想［12］是針對初步確定出的評價指標，以調查征詢的方式向選定的專家提出一系列問題，然后進行統計處理，并反饋咨詢結果。每完成一次提問和回答為一輪，經2～3輪咨詢后，如果專家意見趨于集中，則由最后一輪咨詢確定出具體的評價指標體系。MD方法中專家選擇是關鍵，所選專家必須滿足以下幾點［9］：① 具備決策問題所需的知識和經驗；② 有能力和意愿參與；③ 充足的時間投身該問題研究；④ 有效的溝通技巧等。

（3）分析各指標之間的關聯性，構建ANP網絡結構模型。指標體系中的所有指標組成ANP模型中的元素，這些元素被分為2個部分，第1部分稱為控制層，包括問題目標及決策準則，是一個遞階層次結構；第2部分為網絡層，它是由所有受控制層支配的元素組成，元素之間相互依存、相互支配，形成一個相互依存、有反饋的網絡結構。

（4）求解ANP模型，獲取備選項綜合效用值。首先根據ANP網絡結構模型構造判斷矩陣；再將判斷矩陣組成初始超矩陣；然后對初始超矩陣的元素進行加權處理，得到加權超矩陣；再通過計算極限超矩陣，得到所有元素的權重，即指標體系中各指標的權重；最后結合各備選項的指標值得到其綜合效用值。

2 工程項目管理模式評價模型設計

2.1 建立評價指標步驟

根據本文工程項目實際情況，成立協調小組。協調小組共4名成員，其中高級職稱1名，博士研究生1名，碩士研究生2名。主要任務是擬定研究主題，確定專家咨詢組人員，編制專家咨詢表，組織咨詢并對數據進行統計處理［11］。

2.1.1 確定專家咨詢組人員

根據實際情況聘請了來自政府部門、業主方、咨詢方、施工方、使用／運營單位、學術界等共18名專家，所選專家參加工作年限均超過20a，其中從事建筑或建筑相關行業工作或學術研究的年限超過10a。

2.1.2 構建評價指標體系

通過對與工程項目管理模式評估相關文獻［1－8］進行研究和分析，確保建立的指標體系全面、簡明科學和易于操作，經過2輪調查分析，確立了包含2個層次的評價指標體系。表1所列給出了各指標的統計參數結果，、σ、V、p33和GCR分別表示專家群體意見的集中程度、離散程度、協調程度、一致性以及專家自信度，各參數的計算方法參考文獻［11］的研究。

由表1可知，第2輪所有指標的標準差和變異系數都比第1輪小，即第2輪咨詢中專家給出的判斷分散程度較小，協調程度較高。

文獻［16］將專家的一致意見定義為不少于2／3的專家判斷等級為“大”以上的判斷結果，根據該定義，2輪之后專家形成了一致意見。所構建的評價指標體系包含工程項目目標、工程項目特點、外部環境支持、業主自身能力和業主偏好等5個一級指標，并分別下設若干二級指標。

表1 2輪調查結果統計參數

（1）工程項目目標。傳統意義上的建設工程項目目標是在絕對安全和確保質量的前提下，實現低成本和短工期，所以，必須加強對工程質量、工期和成本的管理和控制。不同項目管理模式有其不同的組織機構［1］，對質量、工期和成本的貢獻程度有較大差異，需根據具體工程要求，選擇合適的項目管理模式。

（2）工程項目特點。我國建設項目呈現大型化、復雜化趨勢，如規模巨大、項目復雜、技術要求高、項目范圍不確定等，選擇的項目管理模式應能與項目的實際情況匹配。因此，從項目規模、項目復雜程度、項目范圍及項目不確定性等二級指標來界定工程項目的實際情況。

（3）外部環境支持。我國工程項目管理水平與國際先進水平還存在一定差距，先進工程項目管理模式應根據當前我國政策和建筑業市場現狀逐步引進 。本文選擇政策支持度、承包商／咨詢方的能力和信息化程度為外部環境支持的下級指標，驗證備選的工程項目管理模式在我國建筑市場的發展態勢。

（4）業主能力。業主方在選擇或者優化現存模式時，應考慮到自身的情況，如經濟保障、技術管理能力和風險處理能力，這里的風險可能來自選擇不當導致的與現存模式之間的沖突，造成資源浪費，也可能帶來內部動蕩和與外部單位合作的不愉快等。

（5）業主偏好。業主方推崇什么樣的合同方式、對設計方案的控制欲望和價值工程的研究熱情都會影響工程項目管理模式的選擇，這里選擇合同方式、對設計的控制和價值工程研究作為業主偏好的二級指標。

2.2 確定指標權重

2.2.1 構建ANP 模型

根據表1所列的工程項目管理模式綜合評價指標體系，分析比較各個指標，得到評價指標之間的相互關聯性。

例如，對于一級指標“工程項目目標”而言，業主希望所選的管理模式能夠最大程度上完成質量、降低成本和縮短工期，但三者的關系是對立統一的，一般情況下不能同時達到“最優”，換句話說，高質量就可能需要延長工期和增大資金投入來實現，壓縮工期可能無法保證工程質量等，因此，C1、C2和C3三者之間存在依賴關系。表2所列展示了各指標間的關聯性。根據指標間的關聯性，構建了工程項目管理模式評價的ANP決策模型，如圖1所示，該模型中各指標之間存在內、外部的依賴關系。

表2 指標間的關聯性

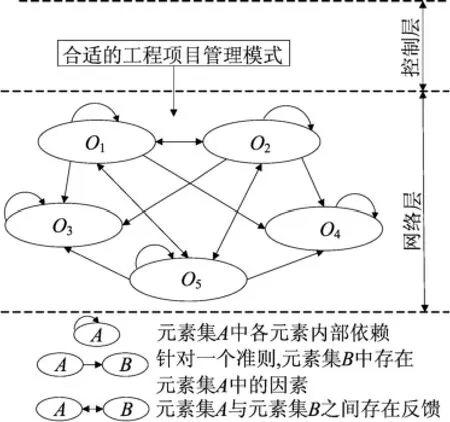
圖1 工程項目管理模式評價的ANP決策模型

2.2.2 計算超矩陣獲取指標權重

設ANP的控制層中有準則或子準則R＝｛R1，…，Ri，…，Rn｝，其中i＝｛1，2，…，n｝，每一個Ri對應一個子網絡圖，運用經典AHP方法求解，得到子網絡圖的權重WR，記WR＝｛WR1，WR2，…，WRn｝。Ri對應的子網絡圖中有元素集，其中，…，｝，k＝｛1，2，…，N｝，mk＝｛1，2，…，mN｝，選擇控制層Ri為準則，進行網絡層相關超矩陣計算。

標度1為針對一個準則（或次準則），兩者的影響程度相同；

標度3為針對一個準則（或次準則），一個比另一個稍微影響大；

標度5為針對一個準則（或次準則），一個比另一個明顯影響大；

標度7為針對一個準則（或次準則），一個比另一個強烈影響大；

標度9為針對一個準則（或次準則），一個比另一個極端影響大；

標度2，4，6，8為上述相鄰判斷的中間過渡含義。

構造判斷矩陣如下：

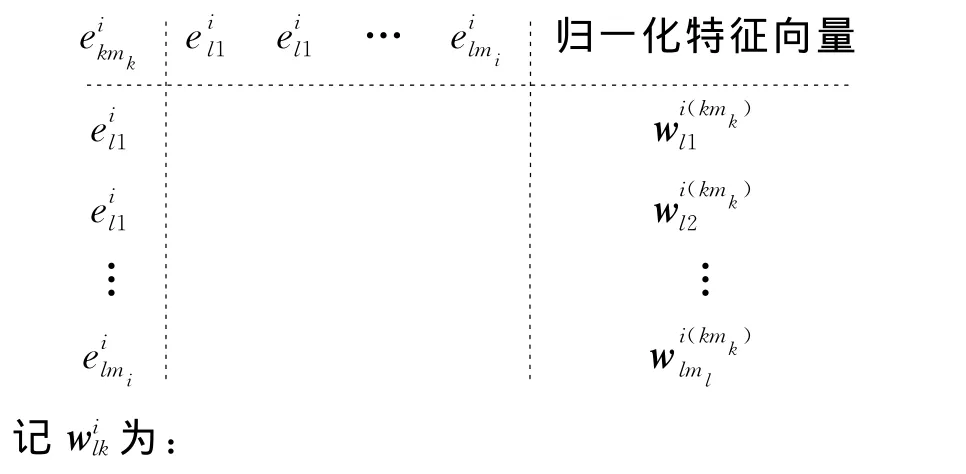
在Ri為準則下，（m1＋m2＋…＋mN）階未加權超矩陣Wi＝（），這樣的超矩陣共有n個，最終可獲得Ri準則下的超矩陣，參見文獻［11］。

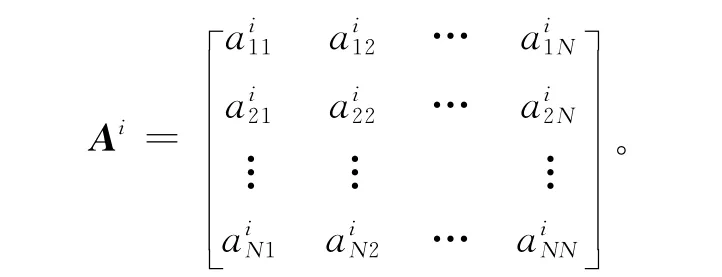
2.3 評價指標值的確定

該模型中各指標均為定性指標，設該決策問題的指標C＝｛C1，…Ci…，Cn｝，備選管理模式M＝｛M1，…，Mj，…，MN｝，其中i＝｛1，2，…，n｝，j＝｛1，2，…，N｝，構造備選模式對指標Ci的貢獻度矩陣如下：

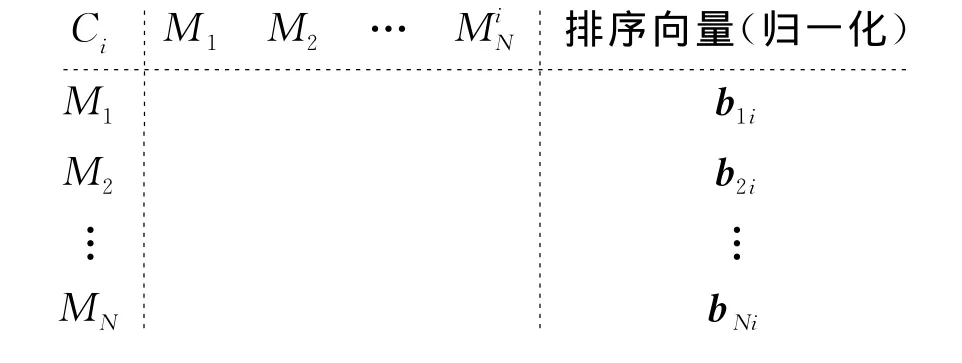
記B為：

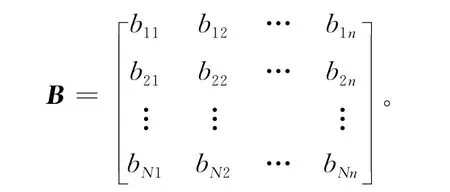
B中的列向量表示各備選模式對指標的優勢度或貢獻度，該值越大，說明針對該指標，選擇該模式更加有效，最后計算備選管理模式的綜合效用值U＝BW。

在實際應用中，應對構造的任何一個判斷矩陣進行一致性檢驗。同時，在指標權重計算和備選模式貢獻度計算中，應對多個專家進行調查，收集較多的信息，通過數值匯總并取其平均值，以減小取值的不確定性。

3 實證研究

某中外合資石化項目建設占地約3km2，總投資額48億美元，工程規模巨大、工藝復雜，為了提高工程項目管理水平，必須選擇合適的工程項目管理模式。

現決策者擬定4種備選的工程項目管理模式，即業主方自行管理的DBB模式、業主方聘請總承包商的EPC模式、業主方參與管理的CM模式及業主方委托的PMC模式。工程項目管理模式綜合評價指標中各指標的重要性各不相同，運用ANP方法確定其權重值。

通過元素集相對于總目標的兩兩比較，得到元素集的加權矩陣，見表3所列。

權重計算過程由Super Decisions軟件完成，根據各指標間的關聯性，構建判斷矩陣，通過多專家打分并計算，組成未加權超矩陣，見表4所列。

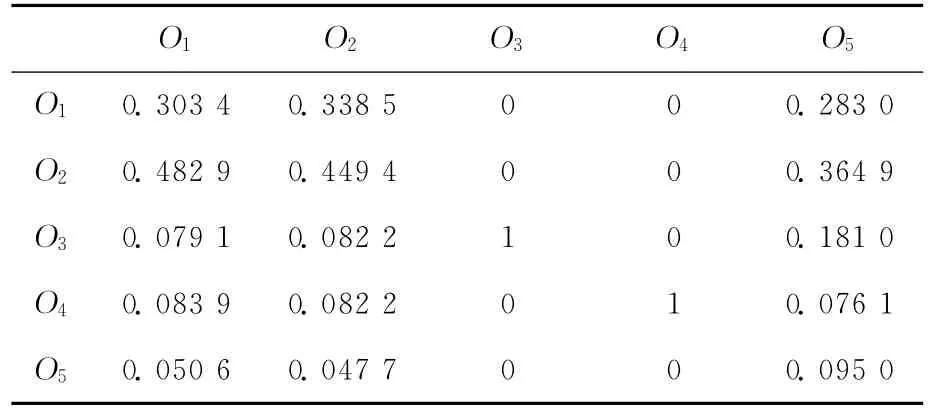
表3 元素組加權矩陣

通過加權矩陣進行加權，得到加權超矩陣，見表5所列。接著計算極限超矩陣，獲得所有指標的最終權重值，見表6所列。由專家打分得到各備選模式對指標的貢獻度即評價指標值，并合成排序，結果見表7所列。

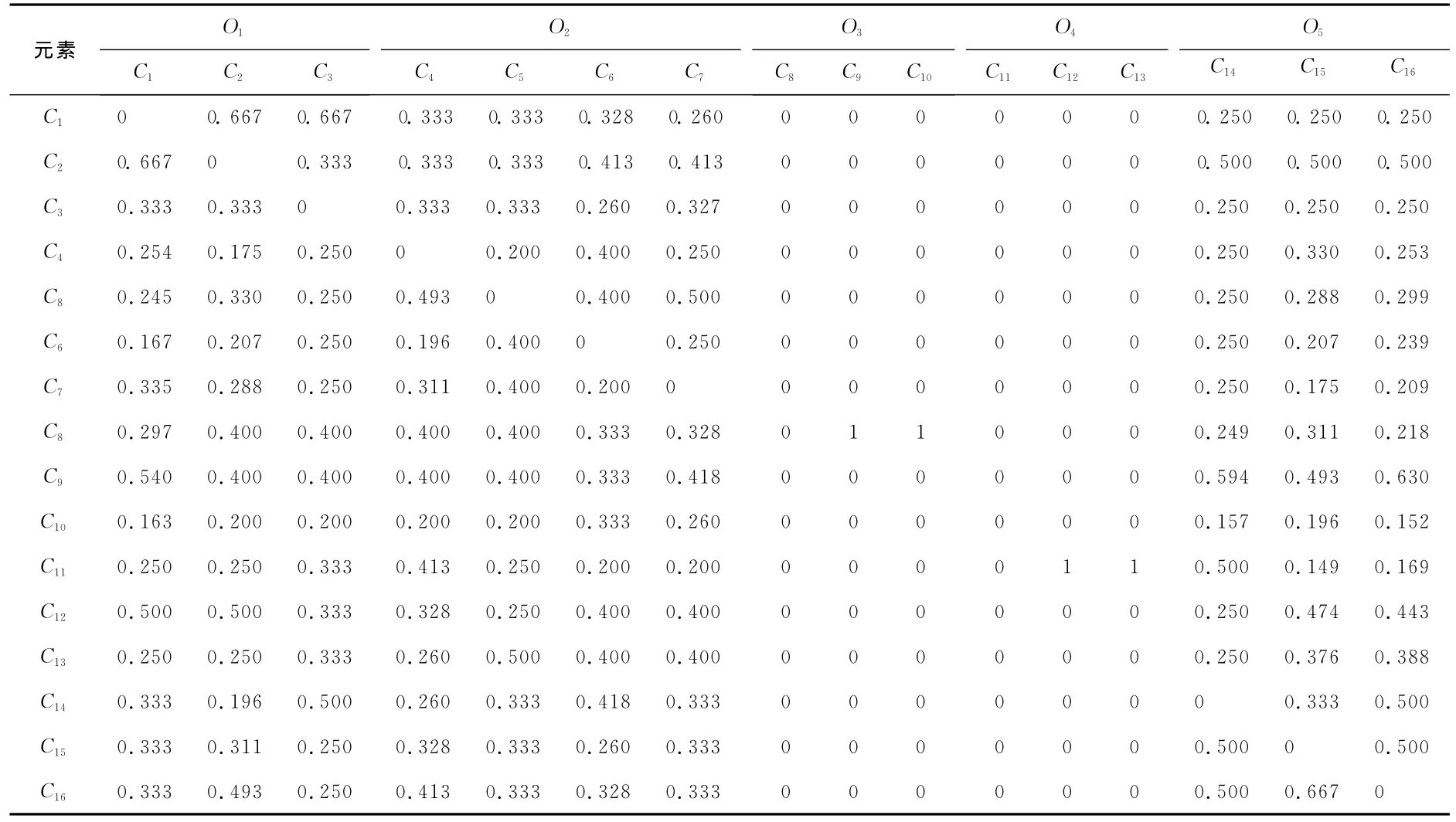
表4 未加權超矩陣

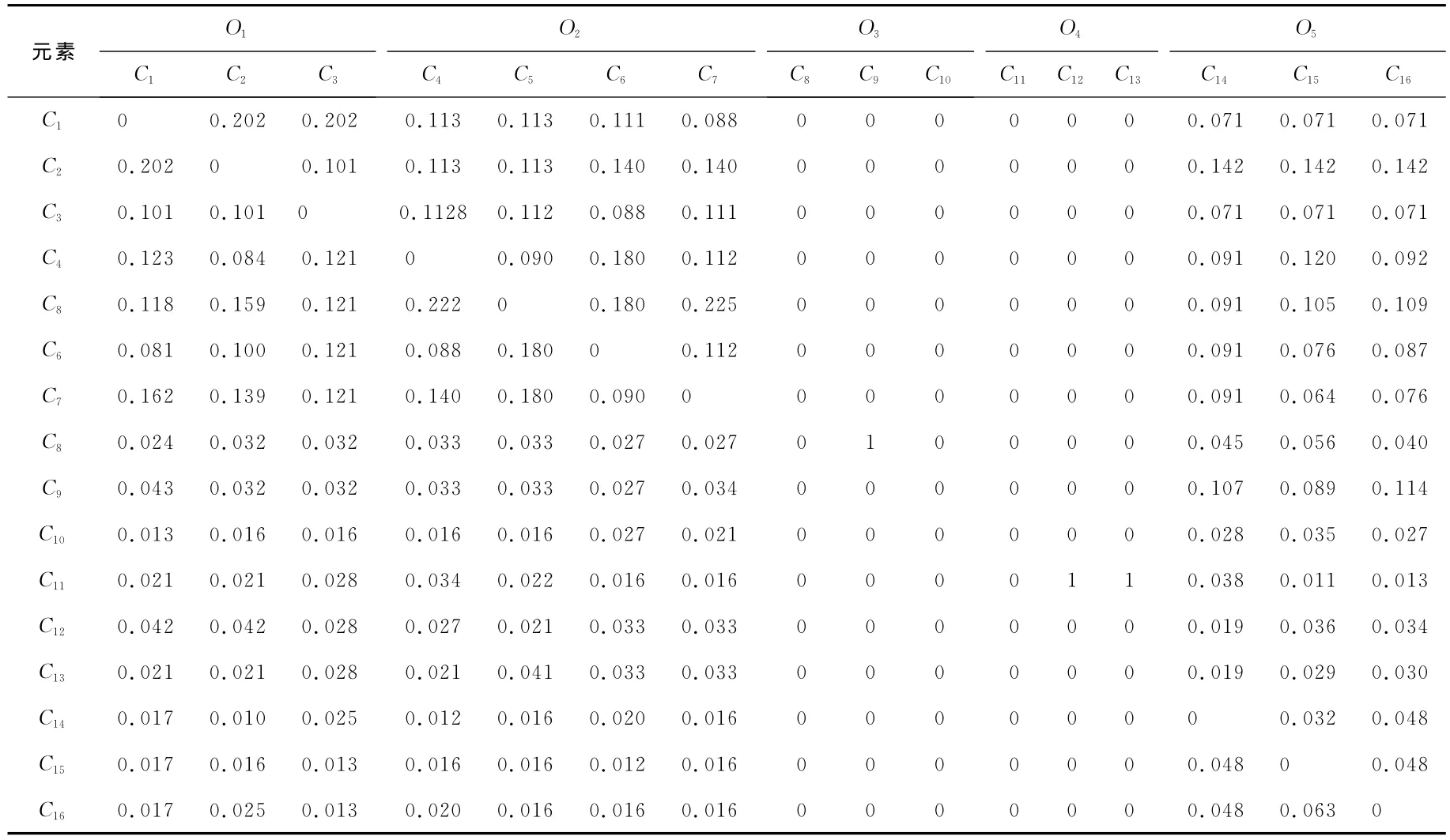
表5 加權超矩陣

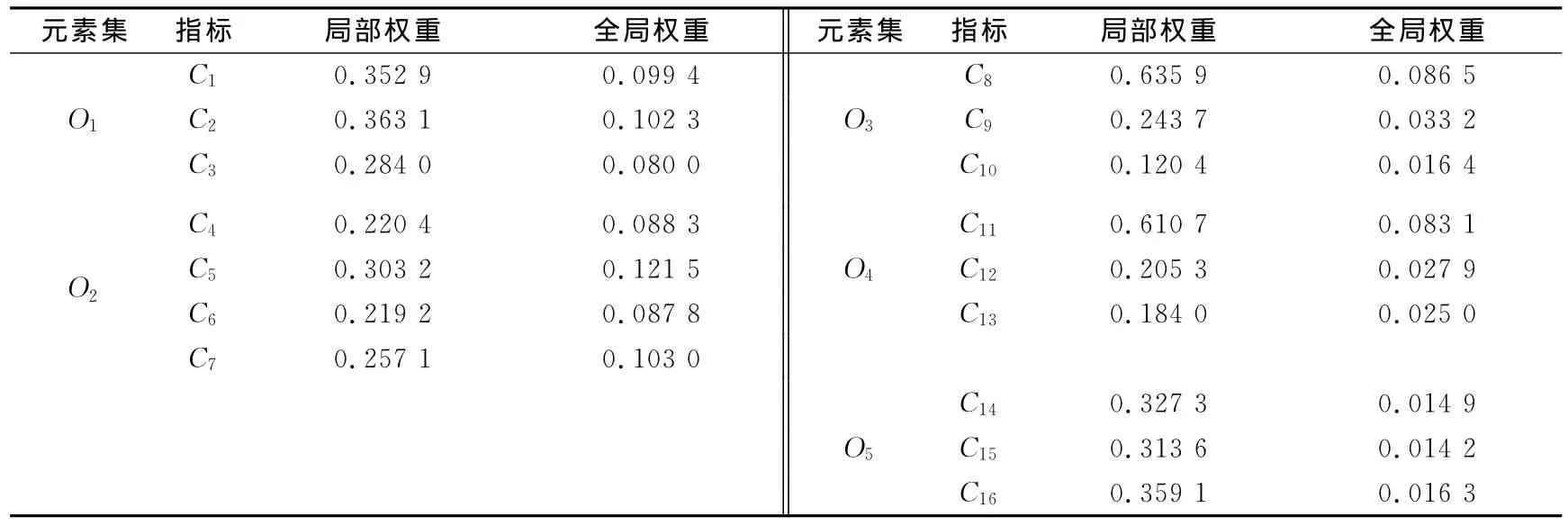
表6 指標權重值

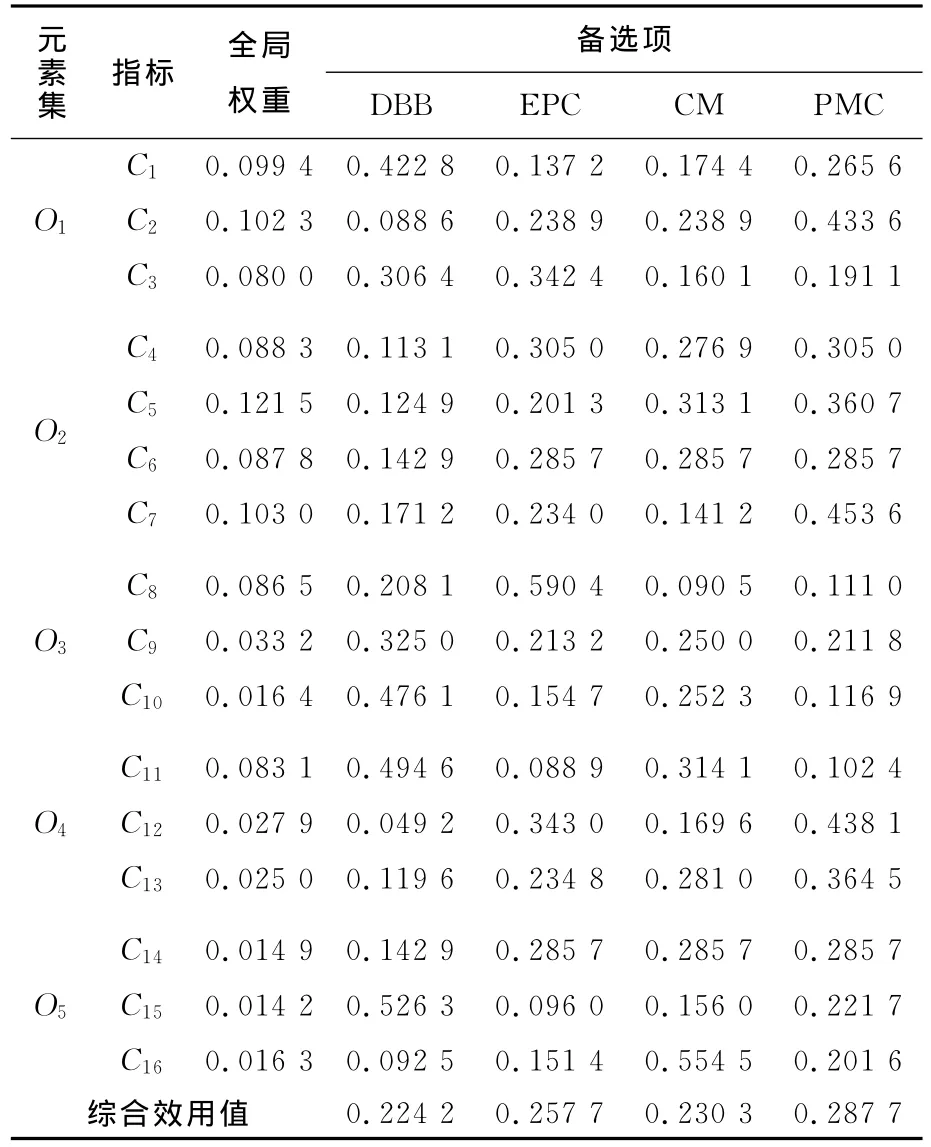
表7 合成排序結果

4個備選工程項目管理模式的綜合效用值是PMC＞EPC＞CM＞DBB，本例中應該選擇業主委托的PMC模式。針對投資額大、工藝復雜的合營工程項目，PMC管理模式在業主融資、資源整合、目標完成等方面都能體現優勢。

4 結束語

本文提出用MD方法建立工程項目管理模式評價指標體系，通過2輪咨詢，確立了5個一級指標和16個二級指標，該方法充分發揮專家的智慧、經驗和知識，具有科學性和可操作性。根據ANP原理構建了指標之間的關聯性模型，并說明了指標權重的定量化計算方法，得到了所有指標的重要性排序。

ANP方法確定指標權重體現了指標體系之間的非遞階層次結構關系，更貼近現實。通過綜合效用值的計算，得到各備選項的優先級排序。本文提出的 MD－ANP方法使評價結果更加科學、穩定，為業主方的決策提供有效的依據。

［1］夏立明，李亞林.國外建設項目管理模式淺析［J］.鐵路工程造價管理，2002（3）：7－10.

［2］Gordon C M.Choosing appropriate construction contracting method［J］.Journal of Construction Engineering and Management，1994，120（1）：196－210.

［3］Al Khalil M I.Selecting the appropriate project delivery method using AHP［J］.Project Manage，2002，20（6）：469－474.

［4］Mafakheri F，Dai L，Slezak D，et al.Project delivery system selection under uncertainty：a multi－criteria multi－level decision aid model［J］.Journal of Management in Engineering，2007，23（4）：200－206.

［5］Moon H S，Cho K M，Hong T H，et al.Selection model for delivery methods for multifamily－housing construction projects［J］.Journal of Management in Engineering，2011（27）：106－115.

［6］惠靜薇.運用模糊層次分析法選擇合適的工程項目管理模式［J］.工業技術經濟，2004（4）：73－75.

［7］曾 陽.基于熵權模糊集的建設工程項目發包模式選擇模型［J］.統計與決策，2009（18）：66－68.

［8］沈詠梅，強茂山，王佳寧.軍隊工程項目管理模式的評價與選擇 ［J］.清華大學學報：自然科學版，2010，50（6）：834－838.

［9］Adler M，Ziglio E.Gazing into the oracle：The Delphi method and its application to social policy and public health［D］.London：Jessica Kingsley Publishers，1996.

［10］Murry J W，Hammons J O.Delphi：a versatile methodology for conducting qualitative Research［J］.Review of Higher Education，1995，18（4）：423－436.

［11］李銀霞，袁修干.改進德爾菲法在駕駛艙顯示系統工效學評價指標篩選中的應用研究［J］.航天醫學與醫學工程，2006，19（5）：368－372.

［12］Xiao J，Douglas D，Lee A H，et al.Delphi evaluation of the factors influencing length of stay in Australian hospitals［J］.International Journal of Health Planning and Management，1997（12）：207－218.

［13］Saaty T L.The analytic hierarchy process［M］.New York：McGraw－Hill，1980：3－100.

［14］Saaty T L.Decision making with the analytic hierarchy process［J］.International Journal of Services Sciences，2008，1（1）：83－98.

［15］Osborne J，Collins S，Ratcliffe M，et al.What“Ideas－about－Science”should be taught in school science？A Delphi study of the expert community［J］.Journal of Research in Science Teaching，2003，40（7）：692－720.

［16］王蓮芳.網絡分析法（ANP）的理論與算法［J］.系統工程理論與實踐，2001，21（3）：44－50.

［17］李玲玲，方 帥，辛 浩.改進的基于層次聚類的模糊聚類算法［J］.合肥工業大學學報：自然科學版，2010，33（6）：859－862.