帶雙參數的四次Wang－Ball型曲線曲面

黃翠玲， 黃有度

（合肥工業大學 數學學院，安徽 合肥 230009）

0 引 言

計算機輔助幾何設計中有很多經典的曲線造型工具，如Bézier曲線、B樣條曲線等，這些曲線模型具有許多優良的性質，在實際工程曲線曲面造型中也得到了廣泛的應用，但仍存在一些不足之處，如給定控制點時，Bézier曲線的位置是確定的，若調整曲線的形狀必須調整控制多邊形。為了方便地調整曲線形狀或改變曲線的位置，人們提出了使用參數構造曲線的方法，有理Bézier曲線和有理B樣條曲線中的權因子也有調整曲線的作用，但權因子的選取對曲線形狀影響尚未完全解決，所以使用張量參數構造曲線的方法是值得研究的重要問題。文獻［1－3］在Bézier基函數中引入1個或多個形狀參數構造了帶參數的Bézier曲線曲面，對Bézier曲線進行了擴展；文獻［4－5］基于引入形狀參數的方法對B樣條曲線作了擴展，使得曲線具有更好的調節性。自1974年，英國數學家Ball在著名的CONSURF機身曲面造型中首次提出一種有理三次參數曲線［6－8］以來，人們發現Ball曲線［9］類似于Bézier曲線，也具有良好的保形性質，且在某些方面有比Bézier曲線更好的性質，因此廣義Ball曲線曲面的研究越來越受到重視，其中以 Wang－Ball和Said－Ball曲線曲面為主。文獻［10－11］分別對三次Ball曲線以及四次Ball曲線進行了參數擴展，由得到的新的基函數組所定義的曲線具有與三次Ball曲線類似的性質。文獻［12］提出2類高次帶位置參數的廣義Ball曲線，第1類介于Wang和Said之間，第2類介于Bézier和Said之間。在此基礎上文獻［13］構造了一簇新的廣義Ball基，并給出了相應曲線和三角面片的一些性質。

本文針對四次 Wang－Ball曲線進行擴展，通過引入2個形狀參數α、β得到5個四次多項式，稱之為 Wang－Ball型基函數。Wang－Ball型基函數實現了從四次 Wang－Ball基到Said－Ball基函數的過渡以及四次Said－Ball基到Bernstein基的過渡，由Wang－Ball型基函數構造了帶有2個形狀參數的曲線，稱為 Wang－Ball型曲線，Wang－Ball型曲線具有與四次Wang－Ball曲線類似的性質，并且包含了文獻［11］中的2類曲線。

1 Wang－Ball型曲線

1.1 基函數的構造及性質

定義1 對t∈［0，1］，α、β∈R，關于t的多項式（1）式為帶參數α、β的四次 Wang－Ball型基函數，即

α＝0，β＝1時基函數的圖形如圖1所示。

上述基函數具有下列性質。

性質1 非負性、權性。對任意的t∈［0，1］，α∈［－2，2］，β∈［－2，1］，有 wi，4（t）≥0，i＝0，1，2，3，4，且

性質2 對稱性。對任意的t∈［0，1］，wi，4（t）＝w4－i，4（1－t），i＝0，1，2，3，4。

性質3 端點性質。

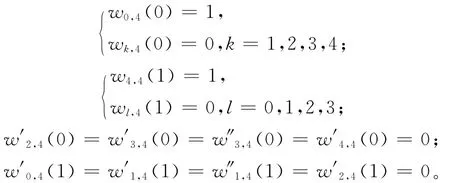
性質4 單峰性。每個基函數在［0，1］上具有唯一的最大值。

性質5 退化性。當α＝0，β＝0時，Wang－Ball型基為四次Wang－Ball曲線的基函數；當α＝1，β＝1時，Wang－Ball型基為四次Said－Ball曲線的基函數；當α＝2，β＝1時 Wang－Ball型基為四次Bernstein基函數。

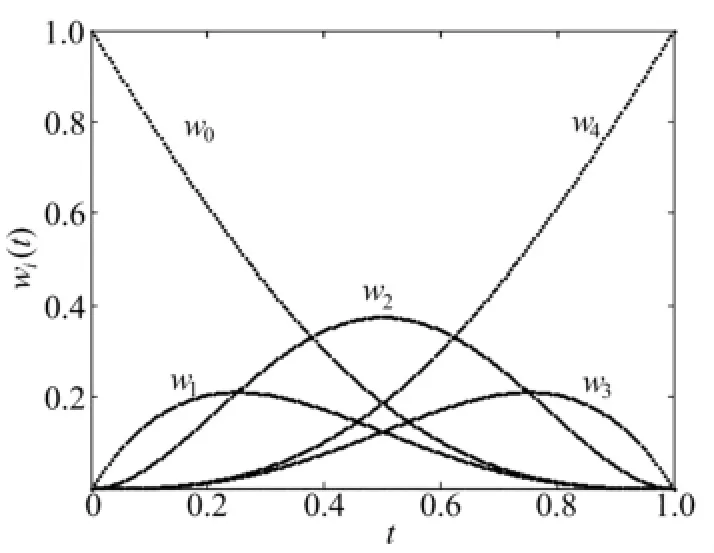
圖1 Wang－Ball型基函數

性質5說明定義1給出的基函數是Ball基函數的擴展。

性質6 對參數α、β的單調性。當t∈［0，1］，w0，4（t）是分別關于α、β的單調遞減函數，w1，4（t）、w3，4（t）是關于α的單調遞增函數，w2，4（t）是關于β的單調遞增函數，w4，4（t）是關于α、β的單調遞減函數。

1.2 Wang－Ball型曲線的構造與性質

定義2 給定控制頂點Pi∈Rd，d＝2，3，i＝0，1，2，3，4，對任意α∈［－2，2］，β∈［－2，1］，稱（2）式為帶雙參數的四次 Wang－Ball型曲線，即

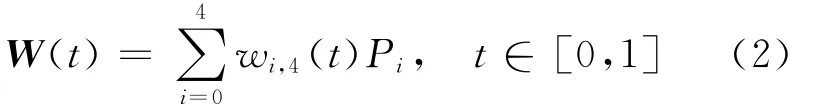
顯然，當α＝β＝0時，四次 Wang－Ball型曲線退化為四次 Wang－Ball曲線；當α＝β＝1時；四次Wang－Ball型曲線退化為四次Said－Ball曲線；當α＝2，β＝1時該曲線退化為四次Bézier曲線。

圖2給出了四次 Wang－Ball曲線以及四次Said－Ball曲線之間的曲線，也給出了四次Said－Ball曲線以及四次Bézier曲線之間的曲線。

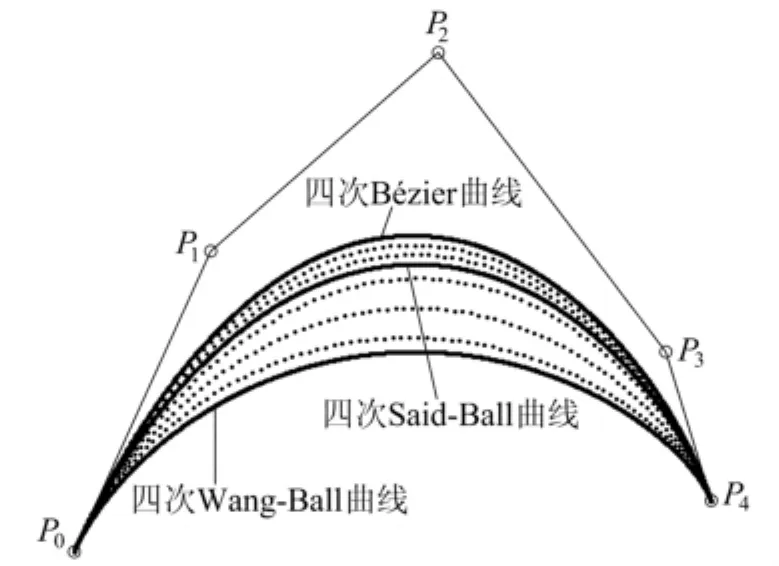
圖2 Wang－Ball曲線與Bézier曲線的過渡

從上述基函數的性質，不難得出曲線具有下列性質。

性質7 凸包性。由基函數的非負性和權性即可得到。

性質8 對稱性。以P0P1P2P3P4和P4P3P2P1P0為控制多邊形的2條四次 Wang－Ball型曲線是相同的，只是方向相反。

因此根據基函數的對稱性質，可得：

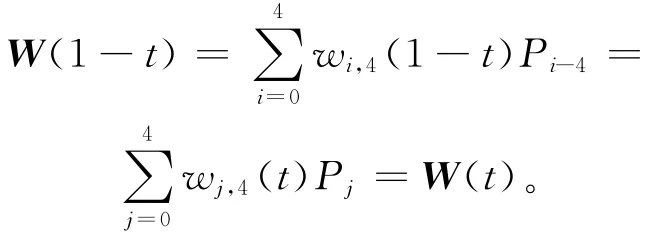
性質9 端點性質。

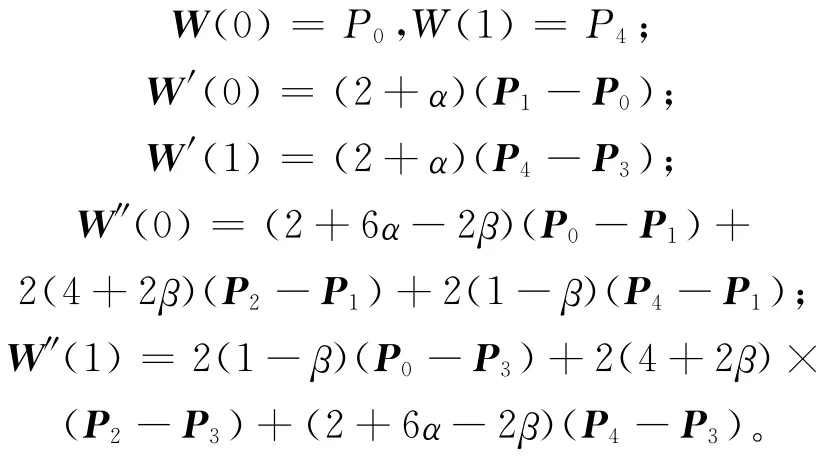
上述端點性質說明四次Wang－Ball型曲線插值于首末端點及與控制多邊形的首末邊相切。

性質10 幾何不變性和仿射不變性。曲線僅依賴于控制頂點，而與坐標系的位置和方向無關，即曲線的形狀在坐標平移和旋轉后不變；同時，對控制多邊形進行縮放或剪切等仿射變化后所對應的新曲線就是相同仿射變化后的曲線。

性質11 逼近性。即當參數α＋β增大時，相應的曲線更加逼近奇控制多邊形，突破了四次Wang－Ball曲線以及Said－Ball曲線對控制多邊形的逼近。根據基函數對參數的單調性可以驗證。

性質12 變差縮減性（V.D.）和保凸性。

性質12的證明可采用文獻［14］中所提供的方法，具體可參考文獻［10］。

1.3 形狀參數的幾何意義

（1）固定參數α，當β變動時曲線的變化如圖3a所示，其中曲線1～4分別為α＝1時，β＝－2，－1，0，1的情形，可看出當α不變，β越大，曲線越靠近頂點P2，即α＋β值越大曲線越逼近控制多邊形。

（2）固定參數β，當α變動時曲線的變化如圖3b所示，其中曲線1～5分別為β＝0時，α＝－2，－1，0，1，2的情形，可看出當β不變，α越大曲線越靠近頂點P1、P3，亦即α＋β值越大曲線越逼近控制多邊形。

圖3 形狀參數的變化情形

2 曲線的拼接

下面討論四次 Wang－Ball型曲線的光滑拼接。設

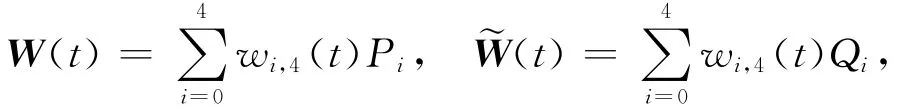
其中，t∈［0，1］；W（t）、～W（t）中的參數分別為α、β和，且－2≤α，～α≤2；－Pi（i＝0，1，2，3，4）為W（t）的控制頂點；Qi（i＝0，1，2，3，4）為～W（t）的控制頂點。

結合四次 Wang－Ball型曲線的端點性質，可得曲線W（t）和～W（t）的光滑拼接條件如下。

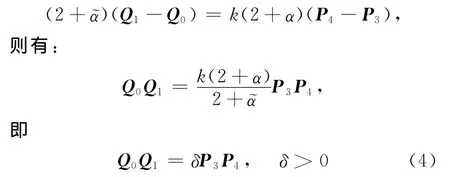
特別地，當 P4＝Q0，且取時，＝W′（1），即2條曲線在切點處不但切向相同，而且切向量相同，則W（t）曲線與曲線在連接點P4處C1連續。

將（4）式帶入（6）式可得：

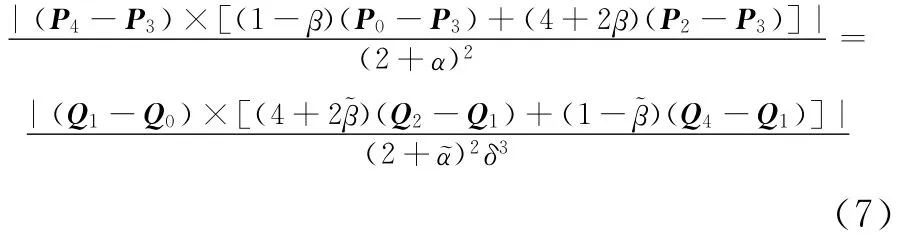
令h1為點P0到P3P4的距離，h2為點P2到P3P4的距離，k1為Q2到Q0Q1的距離，k2為Q4到Q0Q1的距離，當參數α＝1，β＝1時2段端曲線在連接點處G2連續時的情形如圖4所示。

則（7）式變為：

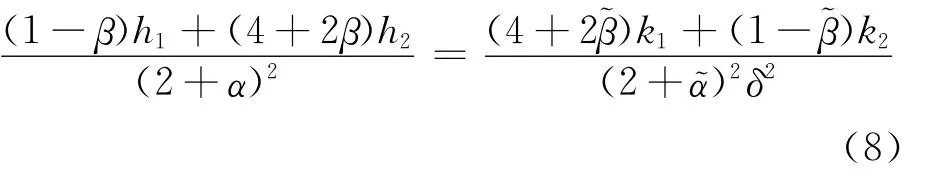
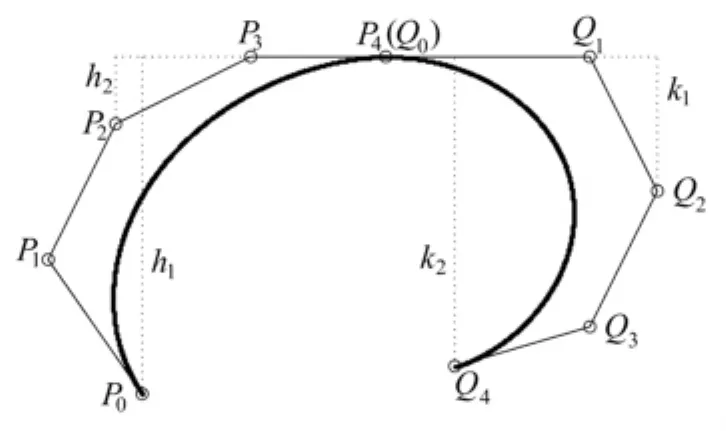
圖4 2段Wang－Ball型曲線的G2拼接

3 曲線的應用實例

3.1 花瓣圖形

Wang－Ball型曲線形成的開曲線花瓣圖形如圖5a所示，參數（α，β）從內到外分別為（－2，－2），（－1.5，－1），（－1，0），（0，0.5），（1，1），從圖5a中可以看出，當α、β取值不同時所形成的圖形仍具有對稱性。

四次Wang－Ball型曲線與四次Ball曲線以及四次Bézier曲線一樣，當首末頂點重合時，得到一封閉曲線，閉曲線的花瓣圖形如圖5b所示，參數（α，β）從內向外分別為（0，0），（1，1），（2，1）。

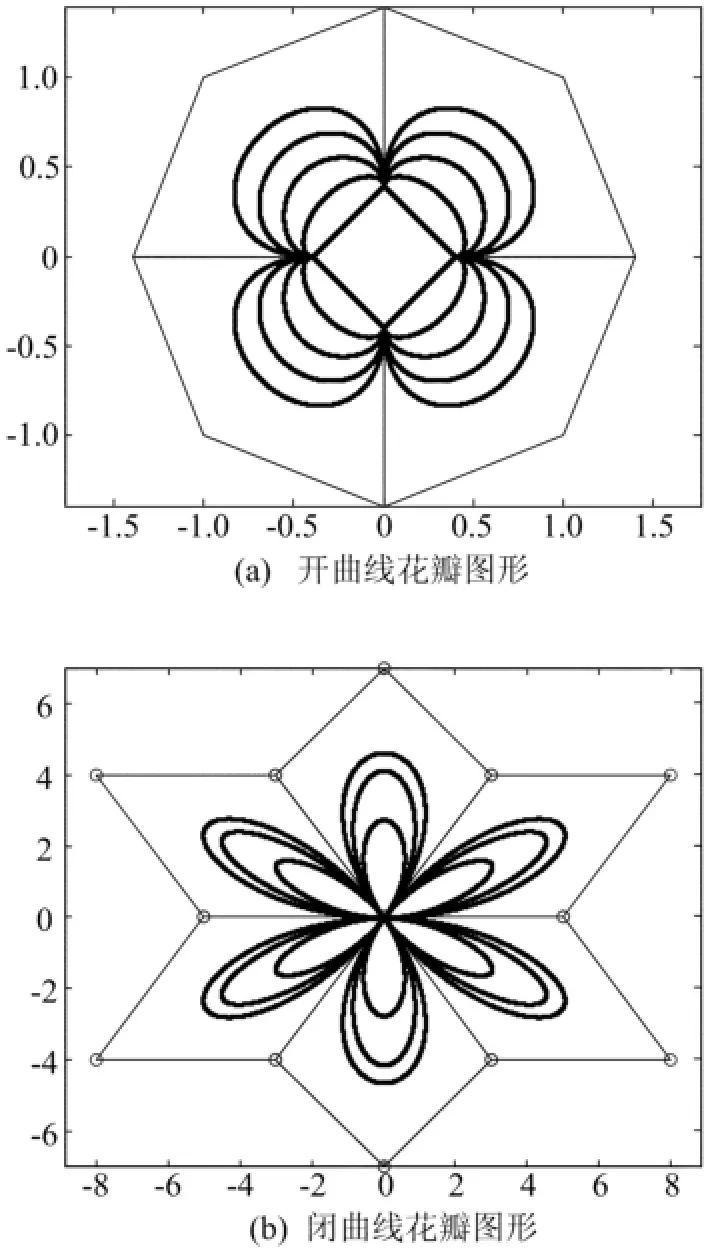
圖5 2種曲線花瓣圖形

3.2 花瓶圖形

圖6a所示為花瓶旋轉曲面的母線，它是由3段相鄰的四次Wang－Ball型曲線以G1連續拼接而成的，圖6b是相應生成的花瓶曲面模型，可以選擇不同的參數，調節母線的形狀，進而調節花瓶的形狀。

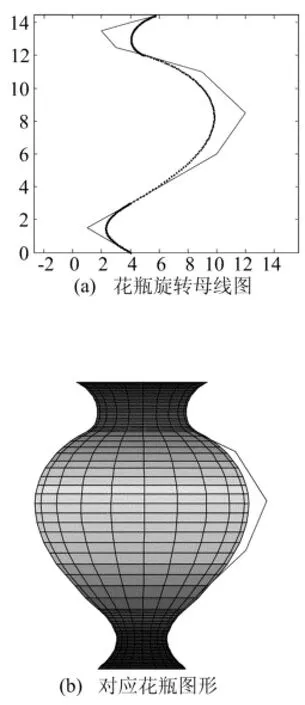
圖6 花瓶圖形

4 張量積曲面

運用張量積的方法可將曲線推廣到曲面上。

定義3 給定5×5個控制頂點Pi，j∈Rd（d＝2，3；i，j＝0，1，2，3，4），其相應的張量積曲面（9）式稱為［0，1］×［0，1］上的雙四次 Wang－Ball型曲面，即

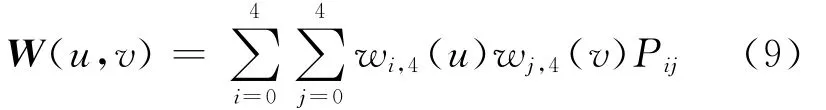
其中，u，v∈［0，1］；α∈［－2，2］；β∈［－2，1］。可以證明雙四次 Wang－Ball型曲面具有與四次Wang－Ball型曲線相似的幾何性質。

5 結束語

由 Wang－Ball型基函數構造的 Wang－Ball型曲線（2）式具有四次Wang－Ball曲線的特征，如端點插值、控制多邊形首末邊相切、凸包性、變差縮減性、保凸性等。該曲線不僅分別以四次Wang－Ball曲線、四次Said－Ball曲線和四次Bézier曲線為特例，而且由于帶有形狀參數，所以可以在不改變控制多邊形的情況下對曲線的形狀和位置進行調整，從而可以得到介于四次 Wang－Ball曲線和Said－Ball曲線之間以及介于四次Said－Ball曲線和Bézier曲線之間的無數中間曲線。本文還討論了2段帶形狀參數的 Wang－Ball型曲線的G0、G1和G2連續的拼接條件。實例表明，Wang－Ball型曲線曲面通過選取不同的參數值可以生成多種不同的常用復雜曲線曲面，因而它在工程曲線曲面的造型中有著非常廣泛的應用前景。

［1］吳曉勤，韓旭里，羅善明.四次Bézier曲線的兩種不同擴展［J］.工程圖學學報，2006，27（5）：59－64.

［2］張元巨，黃有度.帶雙參數的Bézier型三角多項式曲線［J］.計算機應用與軟件，2008，25（11）：236－238.

［3］鄔弘毅，夏成林.帶多個形狀參數的Bézier曲線與曲面的擴展［J］.計算機輔助設計與圖形學學報，2005，17（12）：2607－2612.

［4］王文濤，汪國昭.帶形狀參數的均勻B樣條［J］.計算機輔助設計與圖形學學報，2004，16（6）：783－788.

［5］馬素靜，劉旭敏.二次均勻TC－B樣條曲線的擴展［J］.計算機工程與設計，2008，29（22）：5863－5865.

［6］Ball A A.CONSURF，part 1：introduction to the conic lofting title［J］.Computer Aided Design，1974，6（4）：243－249.

［7］Ball A A.CONSURF，part 2：description of the algorithms［J］.Computer Aided Design，1975，7（4）：237－242.

［8］Ball A A.CONSURF，part 3：how the program is used［J］.Computer Aided Design，1977，9（1）：9－12.

［9］王國瑾，汪國昭，鄭建明.計算機輔助幾何設計［M］.北京：高等教育出版社，2001：99－111.

［10］王成偉.三次Ball曲線的擴展［J］.工程圖學學報，2008，29（1）：77－81.

［11］嚴蘭蘭，饒智勇，溫榮生.兩類新的四次Ball曲線［J］.合肥工業大學學報：自然科學版，2010，33（2）：316－320.

［12］鄔弘毅.兩類新的廣義Ball曲線［J］.應用數學學報，2000，23（2）：196－205.

［13］沈莞薔，汪國昭.Ball基的推廣［J］.軟件學報，2005，16（11）：1992－1999.

［14］Goldman R.金字塔算法：曲線曲面幾何模型的動態編程處理［M］.吳宗敏，劉劍平，曹 沅，等，譯.北京：電子工業出版社，2004：152－157.