旋轉長桿彈侵徹混凝土靶應力波傳播特性研究

趙子龍，唐守政，郭 歡，耿 佳

(太原科技大學應用科學學院，太原 030024)

軍事科技的發展使得傳統的軍事防御工事由地面轉入地下，這也就促使著深層侵徹彈的發展，為了更好的打擊地下防御工事，對旋轉長桿侵徹彈的研究也就成了必然。這項研究對國防工業的發展具有重要的理論與實用的參考價值。

在彈體侵徹厚土或混凝土靶方面的研究已有了大量的成熟的理論和實際研究成果。高世橋等對長桿彈侵徹混凝土靶的問題做了相關研究[1-3];對鎢桿斜侵徹金屬靶的問題李大紅等作了深入探討[4];在圓柱桿侵徹土壤及水泥靶時的應力波傳播特性方面趙子龍等[5-6]已做了相關研究，在此基礎上對旋轉長桿侵徹半無限厚土的動力特性做了進一步研究[7]。在文獻[7]的基礎上，本文利用波動理論建立了縱波的波動方程和扭轉波的波動方程，并利用有限差分法對波動方程進行了數值求解，討論了彈體內部應力波的傳播特性，重點研究了初始旋轉角速度對長桿彈內應力波傳播特性的影響。

1 基本假設

由于長桿彈侵徹混凝土靶的實際問題是非常復雜不便進行數值計算的，這里為了簡化長桿彈侵徹混凝土靶的問題，本文做了如下基本假設:

(1)在計算撞擊力和侵徹位移時，將長桿彈視為剛體，將靶視為流體;

(2)靶響應區介質位移方向與合力方向相同;

(3)對長桿彈侵徹過程的分析與長桿彈中應力波傳播的分析分開;

(4)研究應力波的傳播的過程中，將長桿彈的塑性力學本構關系作線性硬化處理且將應力看作應變的單值函數。

2 侵徹過程

為了研究方便起見，建立兩組坐標系。一組為定坐標系oy，o點為撞擊初始接觸點，y軸沿長桿彈的軸線向下;另一組為動坐標系Crβz，其中C為長桿彈的質心，z沿長桿彈軸線向下，r為極坐標，β為角坐標，r和β一起構成垂直于z的極坐標系統，如圖1所示。取長桿彈與混凝土靶開始接觸時刻作為初始時刻，下面討論長桿彈的運動規律。

2.1 受力分析

如圖1所示，在長桿彈與混凝土靶的接觸表面上任一點A處取一微元dS，該表面上的有法向作用力dFd和摩擦力df，其中df為df1(沿圓周切向摩擦力)和df2(沿母線方向摩擦力)的合力，同時在混凝土靶微表面上作用有等值、反向的力-dF.考慮到高速撞擊過程的特點，將混凝土靶對長桿彈的反作用力看作dFd與df的疊加。

圖1 垂直侵徹示意圖Fig.1 The vertical penetration

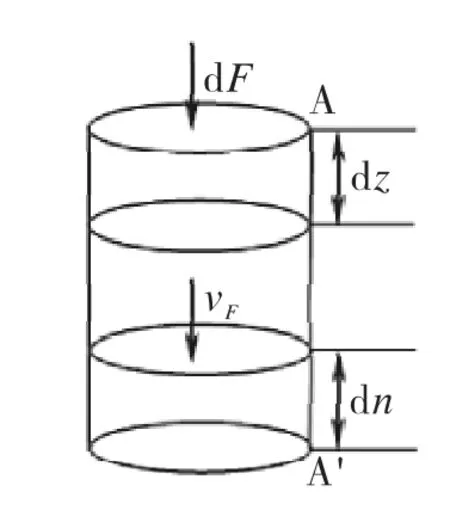
圖2 靶微元的受力及變形示意圖Fig.2 The force and deformation of target element

文獻[4]已得到:

其中，ct為微柱介質的法向擴散速度，vF為微柱介質的合速度。

2.2 靶響應區介質法向擴散速度

擴散速度ct是一個較難確定的參數，根據靶材料質量守恒來確定ct.

由文獻[7]可得到:

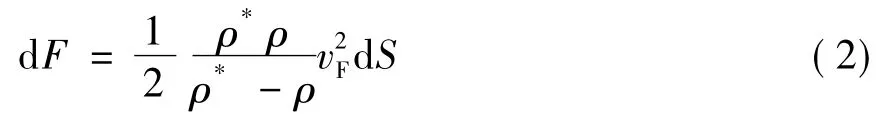
其中，ρ為未響應區介質的密度，ρ*響應區介質的密度。

2.3 長桿彈的動力學方程

設長桿彈的質量和繞軸線轉動慣量分別為mp和Ip，則剛體運動的微分方程為:

其中，SA為長桿彈侵入混凝土靶的表面(是一曲面)，α為長桿彈錐頭部分半頂角，zc表示長桿彈在定坐標系oz中的坐標，符號表示對時間t的二階導數。

由文獻[7]可得到:

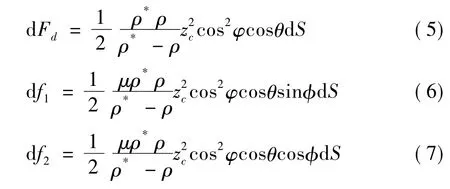
其中，θ為dFd與dF的方向夾角，φ為z與合力dF的夾角，φ為df2與df的夾角。

3 應力波傳播

3.1 波動方程的推導

建立如圖3所示的新的坐標系o1x1.原點o1位于長桿彈的頂部，由于長桿彈在運動，故選取動坐標系o1x1，o1位于長桿彈的錐頂，o1x1軸與軸線重合，隨其一起運動。設長桿彈任一點在縱向變形為u(x，t)，切向變形為 ψ(x，t).

圖3 長桿彈坐標系示意圖Fig.3 The coordinate system of long rod

由位移單值連續條件可以得到連續方程為:

其中v為質點縱向速度，ε為軸向線應變，ω為質點繞軸線的旋轉角速度，γ為扭轉切應變。

在圖3所示長桿彈中取微元體，其受力如圖4所示。

建立運動微分方程:

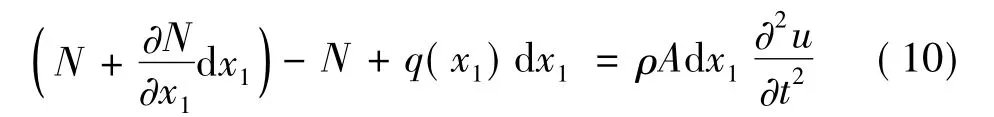
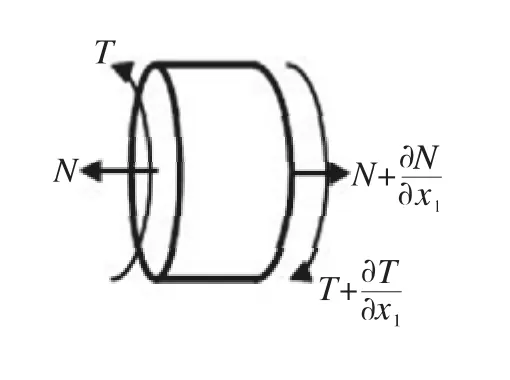
圖4 長桿彈微元受力分析Fig.4 Force analysis of long rod element

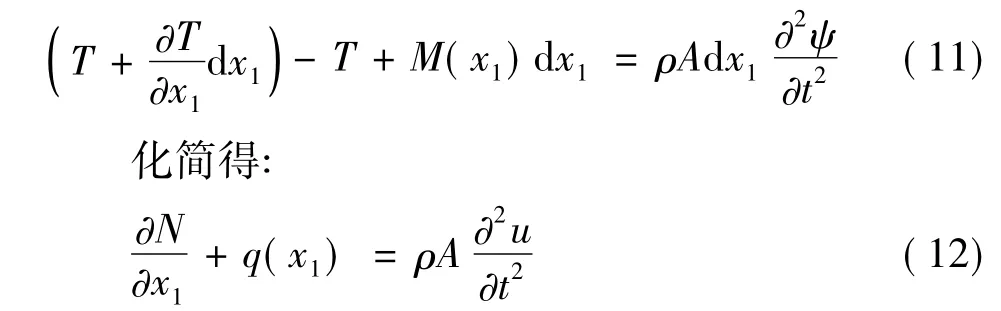
其中，N表示軸力，q(x1)表示沿長度分布的慣性力(由長桿彈的縱向剛體位移引起)，T表示扭矩，M(x1)為沿長度分布的慣性力偶矩(由長桿彈的角位移引起)，ρ為長桿彈的材料密度。由材料力學知識可得:

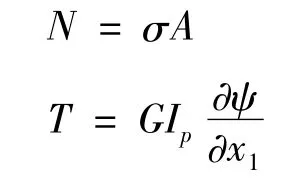
其中，σ為應力，Ip為極慣性矩。將上式代入(12)、(13)式可得到:

長桿彈轟擊混凝土靶的速度大多在1000～2000 m/s之間，也就說是高速撞擊過程。由于長桿彈接觸到混凝土靶的瞬間應力便遠遠超過了屈服極限，因此可以只考慮塑性變形。應力與應變、應變率等許多因素有關，長桿彈的塑性動態本構關系非常復雜。在此，假設應力只是應變的單值函數，且對塑性階段作線性硬化處理，即:

其中，E、G分別為彈體材料的線性硬化模量和切變模量，C為塑性縱波波速，C1為塑性扭轉波波速。

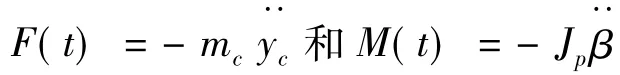
方程(22)和(23)由于增加了運動慣性項，變成了非齊次偏微分方程組，這使得解析求解非常困難。

3.2 波動方程的數值求解

對波動方程(22)和(23)，利用有限差分法進行數值求解。

初始條件和邊界條件:

(1)初始條件

求得軸向正應力和扭轉切應力的一系列數值解，分析和研究在長桿彈中的應力波傳播規律。

3.3 計算結果和分析

進行數值計算時，所選參數如下。

初始條件:

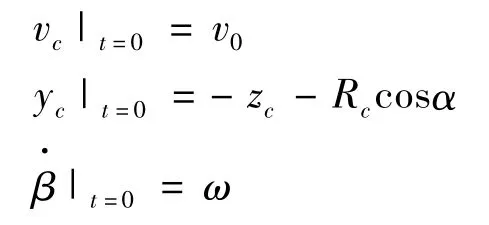
混凝土的密度:ρ=2.13 ×103kg·m－3

混凝土極限密度:ρ*=2.13 × 103kg·m－3

混凝土擠壓極限:σc=80 MPa

長桿彈密度:ρ0=7.8 × 103kg·m－3

長桿彈長度和半徑:L=2000 mm;

Rc=0.1 m

長桿彈材料模量:E=1.26 GPa;

G=0.42 GPa

摩擦系數:μ=0.2

彈頭半頂角:α=30°

彈質心到錐體底面球心距離:

長桿彈的質量:

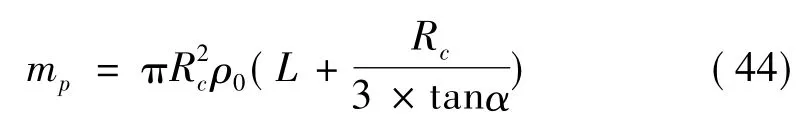
長桿彈繞軸線oy的轉動慣量:

初始速度:v0=1000 m/s

初始旋轉角速度:ω=1 rad/s，10 rad/s，20 rad/s

侵徹位移時程曲線:

撞擊力時程曲線:

應用 MATLAB程序，對式(16)、式(17)、式(22)和式(23)進行數值計算，算出不同ω時的位移、力和應力的數值，進而得到撞擊力、侵徹位移和應力時程曲線如圖5-圖12所示。

圖5 侵徹位移時程曲線(v0=1000 m/s)Fig.5 The history curve of the penetration displacement

由圖5可看出，長桿彈的侵徹位移隨初始旋轉角速度的增加而增大。

圖6 撞擊力時程曲線(v0=1000 m/s)Fig.6 The history curve of force

由圖6可看出:長桿彈的撞擊力幅值隨旋轉角速度的增加反而減小。

圖7 縱向應力時程曲線(ω=1 rad/s，v0=1000 m/s)Fig.7 The normal stress history curve

圖8 縱向應力時程曲線(ω=10 rad/s，v0=1000 m/s)Fig.8 The normal stress history curve

圖9 縱向應力時程曲線(ω=20 rad/s，v0=1000 m/s)Fig.9 The normal stress history curve

由圖(7)-(9)可看出:長桿彈的縱向應力隨旋轉角速度的增加反而減小，且變化較顯著。

圖10 扭轉切應力時程曲線(ω=1 rad/s，v0=1000 m/s)Fig.10 The shear stress history curve

由圖(10)-(12)與圖(7)-(9)的比較可以看出，扭轉切應力遠小于縱向正應力。

圖11 扭轉切應力時程曲線(ω=10 rad/s，v0=1000 m/s)Fig.11 The shear stress history curve

圖12 扭轉切應力時程曲線(ω=20 rad/s，v0=1000 m/s)Fig.12 The shear stress history curve

4 結論

本文主要研究了在旋轉長桿彈撞擊過程中，初始旋轉角速度對撞擊力和侵徹位移的影響，以及對彈體內部應力波的傳播特性的影響。通過研究得到以下結論:

(1)隨著初始旋轉角速度的增大，長桿彈的侵徹位移幅值增大，說明旋轉角速度對侵徹位移有影響。

(2)隨著初始旋轉角速度的增大，長桿彈的撞擊力幅值反而減小。

(3)隨著初始旋轉角速度的出現，縱向正應力明顯減小;隨著旋轉角速度的增大，影響逐漸減小。

(4)扭轉切應力遠小于縱向正應力，在研究應力波傳播時，可以忽略扭轉切應力的影響。

[1]高世橋，曲克波.彈-引系統以極大著角碰擊薄靶板的動力學研究[J].兵工學報，1994(3):85-89.

[2]高世橋，石庚辰，譚惠民，等.彈引系統以極大著角碰擊半無限厚目標時的動力分析[J].北京理工大學學報，1994，14(4):359-365.

[3]高世橋，劉明杰，譚惠民.侵徹彈傾斜侵徹半無限混凝土目標的動力分析[J].兵工學報，1995(4):46-50.

[4]李大紅，吳強，張漢釗，等.鎢桿彈斜侵徹研究[J].爆炸與沖擊，1996，16(2):158-165.

[5]ZHAO Zilong.Stress Wave Propagation on A Cylinder Penetrating into Soil[C]//ICAPV 2000 Proceedings of International Conference Advanced Problems in Vibration Theory and Applications，2000:719-722.

[6]王運葉，趙子龍，圓錐桿斜侵徹水泥靶時應力波傳播特性研究[J].太原科技大學學報，2011，32(4):314-319.

[7]趙子龍，張瑾謹，黃曉瓊.長桿彈侵徹半無限厚土的旋轉效應分析[J].振動與沖擊，2010，29(4):9-11.