常微分方程在數學建模中的應用
李寶萍
(安徽三聯學院 基礎部,安徽 合肥 230601)
常微分方程在數學建模中的應用
李寶萍
(安徽三聯學院 基礎部,安徽 合肥 230601)
本文介紹了常微分方程的發展,數學建模的特點,通過新產品推廣模型、化工車間的通風問題模型、如何確定商品價格浮動規律模型.重點介紹了常微分方程在數學建模中的應用,總結了常微分方程在數學建模中的重要性.
常微分方程;數學建模;模型
1 引言
微分方程作為數學領域的中心學科至今已有近300年的發展歷史,為了尋求、解決類似物體在自由下落過程中下落距離和時間的函數關系;研究火箭在空中飛行時的飛行軌道等這類實際性的問題,往往就要求我們找到滿足某些特定條件的一個或多個未知數方程,為了解決這類實際問題從而產生了微分方程.把含有未知函數及未知函數導數或微分的方程稱之為微分方程.微分方程是在處理實際問題的過程中產生的,微分方程的研究又促進實際問題的解決,同時也促進其他學科的發展.回顧微分方程的發展歷史,我們發現微分方程與物理、化學、醫學、生物學、天文學等方面都有著密切的聯系,特別是科技的飛速發展使得微分方程的應用更為廣泛.
隨著社會和科技的發展,無論是在各學科,還是在各行業均涌現出了大量的、亟待人們去研究和解決的實際課題.這就要求相關的工作人員能靈活地運用數學的思維方法和知識來解決所遇到的問題,從而取得的最大的社會和經濟效益.對復雜的問題進行研究、分析,并發現其中的關系及規律,同時用數學的語言表述出來,把一個實際問題轉化成相關的數學問題,這個問題便稱為數學模型(Mathematical Model),而把建立數學模型的過程稱為數學建模(MathematicalModeling).數學建模是聯系數學和實際問題的紐帶,是數學在相關領域被廣泛應用的媒介,數學建模有很多種分類方法,而微分方程模型是其中的重要一種.微分方程建模在解決很多實際問題時是一種特別有效的數學手段.
2 常微分方程在數學建模中的應用
用常微分方程解決實際問題一般可以分如下幾步:第一步,提出實際問題;第二步,根據實際問題的規律列出相應的微分方程(即建立數學模型);第三步,解出微分方程或者對方程進行進一步定性分析;第四步,通過方程的解(或性質)來解釋或者預測實際問題的發展,也就是通過數學語言來描述實際現象.下面由不同領域的幾個例子來介紹常微分方程在數學建模中的廣泛應用.
2.1 新產品的推廣模型
在管理和經濟學中,我們經常會研究關于經濟量的增長、變化和邊際等方面的問題,我們一般可以結合實際,再建立相應的微分方程模型,從而尋找出經濟量的變化發展規律并做出相應的預測和決策,新產品的推廣模型是經濟學中常見的一種數學模型,下面我們來做些簡要的介紹:
假設有一種新產品現在要推向市場,t時刻的銷量為x(t),由于產品的性能較好,每個產品都是一個宣傳品,因此t時刻產品銷量的增長率與x(t)成正比,同時,考慮到產品的銷售會存在一定的市場容量N,統計表明,與尚未購買該產品的顧客潛在的銷售數量N-x(t)也成正比,于是有
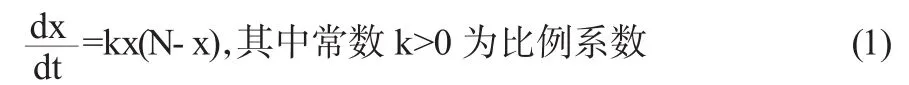
通過分離變量、兩邊積分,可以解出

方程(1)稱為邏輯斯諦模型,通解表達式(2)稱為邏輯斯諦曲線,由
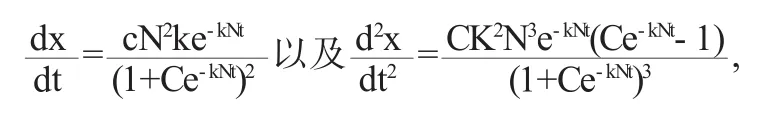
國內外很多經濟學家根據調查表明,很多產品的銷售曲線與公式(2)的曲線十分接近,按照對曲線的性狀分析,專家認為:在新產品推出的初期階段應采取小批量的生產并加強廣告宣傳力度;在產品用戶達到20%至80%階段,產品應采取大批量的生產;而在產品用戶超過80%時,應做適時轉產,這樣才能達到最大的經濟效益.
2.2 化工車間的通風問題模型
由于化工生產過程中,經常要排出一些不利于環境的物質.為了保持車間內的環境衛生,必須通入大量的新鮮空氣,這就是通風問題.
設有一個30×30×12m3的車間,其中空氣中含有0.12%的CO2,如需要在10分鐘后CO2的含量不超過0.06%.(設新鮮空氣中CO2的含量為0.04%),問每分鐘應通入多少m3的新鮮空氣?
解 引入下列符號:
y——時間t時CO2的濃度;
a——通入的空氣量[m3/min];
v——車間的體積[m3];
y0——CO2的初濃度;
g——新鮮空氣CO2的濃度;
解決這個問題主要依據下列兩個物質平衡式:

現在考慮在時間間隔[t,t+dt]內CO2的進入量與排出量.由(2)式知
CO2的進入量=agdt
CO2的排出量=aydt
在瞬間t,CO2的總量等于vy;在瞬間t+dt,CO2的總量等于v(y+dy).所以在dt這段時間內,CO2的增量為v(y+dy)-vy=vdy.
根據上述分析,由(1)式可得 vdy=agdt-aydt

上述方程是一階變量可分離方程.顯然初始條件是y|t=0=y0.容易求解得

上式就是這個車間中空氣中CO2的濃度y與時間t的函數關系.
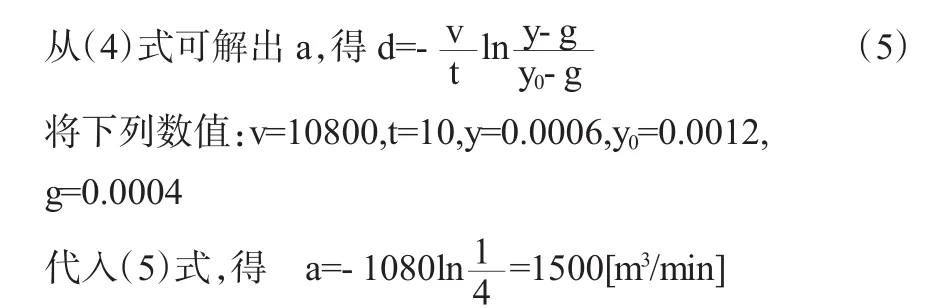
也就是說每分鐘應通入1500[米3]的新鮮空氣,就能在10分鐘后,使車間內的CO2含量不超過0.06%.
實際上所需的新鮮空氣量,比上面的數要小.因為新鮮空氣并不是象假設那樣很快地與混濁空氣混合,而是逐步地與混濁空氣混合,并且在很大程度是將它排擠出去的.
2.3 如何確定商品價格浮動規律模型
設某種商品的供給量Q1與需求量Q2是只依賴于價格P的線性函數,并假定在時間t時價格P(t)的變化率與這時的過剩需求量成正比,試確定這種商品的價格隨時間t的變化規律.

其中a、b、c、d都是已知的正常數.(1)式表明供給量Q1是價格P的遞增函數;(2)式表明需求量Q2是價格P的遞減函數.
當供給量與需求量相等時,由(1)與(2)求出平衡價格為

容易看出,當供給量小于需求量時,即Q1 由假定知道,P(t)的變化率與Q2-Q1成正比,即有 其中 k=α(b+d),h=α(a+c),都是正的常數. (3)式是一個一階線性微分方程.求通解如下: 如果已知初始價格P(0)=P0,則(3)式的特解為: 上式即為商品價格隨時間的變化規律. 常微分方程理論在數學建模中的廣泛應用,將數學理論方法和生活實際巧妙地結合了起來,給人們提供了一種解決問題的嶄新的思維方式.在解決實際問題的過程中應用微分方程理論所建立的數學模型,一般都是動態的數學模型,整個推導過程相當繁雜,但是結果極其簡明,還是能提供給人們合理的解釋.因此如果能有機地將常微分方程理論與數學建模結合起來,必定能使常微分方程理論在實際應用過程中發揮更大的作用、解決更多的實際問題,從而產生更好的經濟效益. 〔1〕王高雄.常微分方程(第二版)[M].北京:高等教育出版社,1983. 〔2〕姜啟源.數學模型(第二版)[M].北京:高等教育出版社,1993. 〔3〕李心燦.高等數學應用 205例[M].北京:高等教育出版社,1997. 〔4〕郭爽,侯麗英,李秀麗.常微分方程在數學建模中的應用[J].數學教學研究,2009(4):57-60. 〔5〕歐陽瑞,孫要偉.常微分方程在數學建模中的應用[J].宿州教育學院學報,2008(2):146-147. O172 A 1673-260X(2012)11-0-001-02 安徽三聯學院2010年度院級質量工程項目(10ZIGC004)
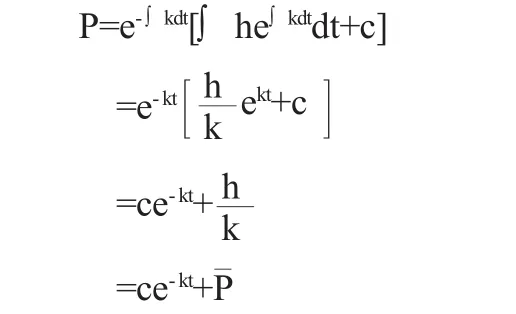
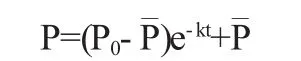
3 結束語

